向量分析
向量分析是构成许多物理和数学模型的基础. Wolfram 语言可以在各种坐标系统对梯度、散度、旋度和拉普拉斯算子进行基本的运算. 而且，这些运算子是以非常一般的形式实现的，这样允许它们被用于不同的维度以及具有更高的阶数的张量中.
向量导数
| Grad[f,{x1,…,xn}] | 标量函数  的梯度 |
| Div[{f1,…,fn},{x1,…,xn}] | 向量值函数  的散度 |
| Curl[{f1,…,fn},{x1,…,xn}] | 向量值函数的旋度 |
| Laplacian[f,{x1,…,xn}] | 标量函数  的拉普拉斯算子 |
虽然这些运算符可用于任何维度，但是它们常用于三维计算中.
旋度不限于三维. 以下给出两维的旋度，它是一个标量：
一般来说，维度为
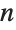
的向量的旋度是阶数为
的完全反对称张量：
在维度不是3中的旋度的意义将在下一个子章节中有更多的讨论.
推广至高阶张量
所有在前面章节介绍的四个运算符是一般的运算符可以把向量和高阶张量作为输入. 对于维数为
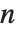
的
Curl，输入可以为标量、向量或阶数高达
的张量. 对于其他函数，输入张量所允许的阶数是无限制的.
向量的梯度是一个2阶张量. 每个额外的梯度会提高一个阶数：
散度是求梯度后对后两个
“槽
”的缩并. 因此阶数减1：
拉普拉斯算子保留阶数，因此向量的拉普拉斯算子是另一个向量：
产生该行为的原因是旋度是反对称梯度的 Hodge 对偶. 以下解释了阶数的限制：
已知的坐标图表
Wolfram 语言 含有关于大量坐标图表的信息. 函数
CoordinateChartData 提供令人提取这些信息的机制.
以下例子显示如何查询可用的坐标图表. 在最普遍的格式中，坐标图表规范包含坐标系统名称、度量和一个维度. 请注意，许多图表需要参数，你可以指定也可以留给显示的默认值.
以下给出3维直角坐标系的 Wolfram 语言的标准名称：
用符号
All 替代度量
"Euclidean" 则包含了非欧氏的坐标图表：
虽然坐标图表的标准名称很长，当使用欧氏坐标图表时，一般可以省略
"Euclidean" 和维度.
CoordinateChartData 包含许多关于不同坐标图表的属性. 最基本的是度量，它最终决定坐标图表中的所有长度和体积. 然而在正交坐标上的向量分析中，比较常用的是考虑比例因子和体积因子.
以下提取在点
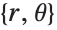
上的极坐标度量：
以下沿曲线
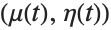
给出椭圆坐标的比例因子. 请注意，这里使用了默认参数
：
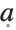
比例因子将坐标速度
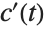
与物理速度相关联.
物理速率是速度的模. 这个也可以从度量和坐标速度中直接获取：
以下给出双极坐标的体积因子，参数设为1. 请注意需要用双列表确保1被认为是参数，而不是维度：
非直角坐标系中的向量导数
四个向量导数运算符可用于任何坐标图表. 只需要在函数的第三个参变量中指定图表.
| Grad[f,{x1,…,xn},chart] | 在指定坐标图表中的梯度 |
| Div[{f1,…,fn},{x1,…,xn},chart] | 在指定坐标图表中的散度 |
| Curl[{f1,…,fn},{x1,…,xn},chart] | 在指定坐标图表中的旋度 |
| Laplacian[f,{x1,…,xn},chart] | 在指定坐标图表中的拉普拉斯算子 |
在这些命令中数组被视为正交基中的分量. 这适用于输入和输出. 这样，物理点乘可用
Dot 计算.
在正交坐标系统中，标量的梯度等于偏导除以比例因子：
向量的梯度和高阶张量引入了对结果的连接项，意味着它不只是每个分量的梯度：
既然散度只适用于向量和张量，所以它总有连接项. 然而，因为数组在正交基中被处理，所以散度仍然是求梯度后缩并：
根据定义，拉普拉斯算子是梯度的散度. 因此拉普拉斯算子在非直角坐标系中也有连接项：
这意味着，向量拉普拉斯算子不只是每个分量的拉普拉斯算子：
当作用于标量时，没有连接项，但是比例因子的正规化并没有出现在结果中：
经典定义
如上所述，正交坐标中的标量梯度包含偏导数和比例因子. 就比例因子和体积因子而言，一个向量的散度、一个标量的拉普拉斯算子以及一个向量的旋度有类似的定义.
正交图表中梯度通过比例因子与直角坐标中的梯度相关：
在正交坐标系统中，一个向量的散度的经典公式与使用比例因子和体积因子的直角坐标中的散度相关：
合并散度的经典公式和正交系统中标量的梯度定义会产生拉普拉斯算子的经典公式：
以下举例说明了一个向量的三维旋度的类似公式. 若要推广至维度
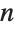
，用
scales 的
份拷贝的
TensorProduct 替代首位的
scales：
维欧氏图的标准名称 
维欧氏空间中可用的坐标图表
维空间中可用的坐标图表