 |
BUILT-IN MATHEMATICA SYMBOL
ExponentialMovingAverage
ExponentialMovingAverage[list, 
]
gives the exponential moving average of list with smoothing constant .
Details
- The smoothing constant is typically a number between 0 and 1, but can be any expression.
- ExponentialMovingAverage[x, ] generates a list of results
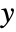in which 
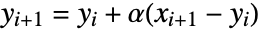. » - The output from ExponentialMovingAverage[list, ] has the same length as list.
- ExponentialMovingAverage handles both numerical and symbolic data.
- ExponentialMovingAverage works with SparseArray objects. »
New in 6
