WOLFRAM

Wolfram SystemModeler Documentation Center
Wolfram言語ホームページ »

Modelicaの諸相とモデリングについての助言

初期化多体ライブラリ(MultiBody Library)
状態一般的な助言
イベント

本章では，Modelica言語の重要な諸相について紹介し，System Modeler を使う際に留意するべき点について助言する．

初期化

モデルのシミュレーションの開始時にはモデルを初期化しなければならない．初期化には積分の問題よりも多くの変数の値の計算が含まれるのが普通である．特に，積分の際に計算される変数に加え，状態，fixed=falseのパラメータ，離散変数のpreの値が計算されていなければならない．

System Modeler には，次の3つの異なる種類の初期化を検出することができる．

Start属性

Modelicaに含まれる変数はすべてstart値を持つ．変数のstart値を指定しないとデフォルト値が使われる．デフォルト値は変数のタイプによって異なる（0.0はReal，0はInteger，falseはBoolean）．

start値は，変数を厳密にその値に初期化する，あるいは非線形系で解かれた変数の推定値として使うことができる．SimulationCenterの変数のVariablesタブで，start値とその使われ方を見ることができる．

モデルに劣決定の初期化が含まれている場合，方程式の数が少なすぎるのでSystem Modeler は開始値から初期化する変数を選ばなければならない．System Modeler は，モデルの方程式構造に基づいて，どの変数が開始値から初期化できるかを調べ，最適であると判断した変数を選ぶ．System Modeler は，指定されたstart値を持つ変数がよりふさわしく， 状態変数が他の変数よりもふさわしいと判断する．例えば，以下の「model A」では，xがそのstart値に初期化される．

model A
  Real x(start = 1);
equation
  der(x) = -x + 1;
end A;

start値が推測値として使われた場合は，求める解を得る助けになる．z=2とz=3の2つの解を持つ方程式 z2-6=zについて考えてみよう．以下の「modes B1」と「modes B2」を見ると，初期設定によって求まる解が異なることが分かる．

model B1
 Real z(start = 4);
equation
 z^2 = 6 - z;
end B1;
model B2
 Real z(start = -5);
equation
 z^2 = 6 - z;
end B2;

初期方程式とアルゴリズム

初期化で値を設定する最も簡単な方法は，初期方程式あるいは初期アルゴリズムを使うことである．

model C
  Real x;
initial algorithm
  x := 1;
equation
  der(x) = -x + 1;
end C;

「model C」では，x の値は常に1から始まるのに対し， 「model A」では，xの開始値はモデルの構築後に，修正によって，あるいはSimulationCenterで変えることができる．初期方程式のセクションを修正によって変えることはできない． 初期方程式のセクションは，方程式を使って開始値が計算できるので，開始属性よりも強力である．例えば，「model D」の変数xは，初期方程式でder(x)=0が使われているので定常状態から始まる．

model D
  Real x;
  Real y(start = 3);
initial equation
  der(x) = 0;
equation
  der(x) = -x + y + 1;
  der(y) = -y +2;
end D;

Fixed属性

変数宣言にfixed属性を加えて，変数を厳密にそのstart値に初期化すべきであると宣言することができる．これは，事実上，初期方程式を与えることと同じである．しかし，fixed=trueを使っていてstart値が文字通りの数である場合は，シミュレーションの構築後にSimulationCenterのVariablesタブでこれを変更することができる．以下の「HelloWorld」と「HelloWorldInitialEquation」の2つのモデルでこの違いを見ることができる．

model HelloWorld
  Real x(fixed = true, start = 1.0);
equation
  der(x) = -x;
end HelloWorld;
model HelloWorldInitialEquation
  Real x;
initial equation
  x = 1.0;
equation
  der(x) = -x;
end HelloWorldInitialEquation;

パラメータについては，fixed=falseと設定してパラメータが初期化中に計算されるべきであることを示すことができる．以下のモデル「HelloWorldParameter」では，指数関数の減衰定数が初期化で計算されるパラメータである．これは，xの開始値の2倍に指定されている．

model HelloWorldParameter
  Real x(start = 1.0, fixed = true);
  parameter Real k(fixed = false);
initial equation
  k = 2*x;
equation
  x = -k*der(x);
end HelloWorldParameter;

When節と初期化

初期化に際しては，When方程式とWhen文には特別の規則がある．When節はその条件としてinitial()を含んでいる場合にのみ初期化中にアクティブになる．したがって，initial()のないWhen方程式とWhen文については，変数の割当てのために初期方程式を追加する必要がある．

model WhenExample
  Integer x;
algorithm
  when sample(2.01, 5.0) then
    x := 1;
  elsewhen sample(0.5, 0.1) then
    x := pre(x) + 1;
  end when;
end WhenExample;

「model WhenExample」を構築するときは，System Modeler は初期化が劣決定であることを指摘して，（Integerのデフォルトの開始値である0という）start値からの初期化にxを選んだことを告げる．

model WhenExampleInitial
  Integer x;
algorithm
  when {initial(), sample(2.01, 5.0)} then
    x := 1;
  elsewhen sample(0.5, 0.1) then
    x := pre(x) + 1;
  end when;
end WhenExampleInitial;

「model WhenExampleInitial」は，最初のWhen条件リストにinitial() を加えることで劣決定の初期化が修正されている．劣決定の初期化は，初期方程式を加える，あるいはxの宣言にfixed=trueを加えることでも修正することができる．

状態

System Modeler の状態は，System Modeler が数値積分で計算するために選んだ変数のことである．このために，System Modeler には変数の微分のための方程式がなくてはならない．しかし，モデル中で微分が発生するすべての変数が状態になるわけではない．シミュレーションの安定性のために，System Modeler は状態となる変数を一定数選ぶ．ある意味では，これらの変数はシミュレーションを操縦する変数と見ることができる．

これらの変数は，微分はされるが，状態の実際の値は数値積分以外の方法で計算されるので，選択はされない．System Modeler は，モデルの変換の間に，もとのモデルにはない新たな微分を導入することもでき，新たに微分された変数が状態として選ばれることも可能である．

System Modeler は「index reduction」と呼ばれる手法を使って可解形式についての方程式を生成する．これには選択された方程式系の微分が含まれる．どの方程式を微分するかは「Translation(変換)」セクションのオプションにあるindex reduction (索引削減)のログで見ることができる．同じウィンドウで選択した状態のログを見ることもできる．index reductionログおよび選択した状態のログは，SimulationCenterのビルドログで見ることができる．

動的状態選択

System Modeler がモデルの変換中に好ましい状態の集合を見付けられないことがある．このような場合には，2つの状態候補を選び，シミュレーション時にどちらを状態にするかを決定する．これは，シミュレーションのある部分で1つの状態が使われ，別の部分ではもう一方の状態が使われる可能性があることを意味する．これは「動的状態選択」と呼ばれる．動的状態選択がどちらかを選べる状態候補の変数は「動的状態」と呼ばれ，動的ではない状態は「静的状態」と呼ばれる．

モデルによっては動的状態選択が必要なものもある．以下の「model Pendulum」を例として挙げる．これ以外のモデルについて，System Modeler が必要ではない場合にも動的状態選択を使うことがあるかもしれない．そのようなモデルについては，以下に示したstateSelect属性を使って，System Modeler にどの状態を選ぶべきかのヒントを与えることができる．

model Pendulum
  parameter Real m = 1;
  parameter Real L = 1;
  parameter Real g = 9.82;
  Real vx;
  Real vy;
  Real F;
  Real x(start = 1/(L*sqrt(2)));
  Real y(start = 1/(L*sqrt(2)));
equation
  m * der(vx) = -(x / L) * F;
  m * der(vy) = -(y / L) * F - m*g;
  x * x + y * y = L * L;
  der(x) = vx;
  der(y) = vy;
end Pendulum;

選択状態のログがオンにしてあると，ログは動的状態候補を静的状態とは区別して，実際にいくつの状態が候補から選ばれたかを伝える．上のPendulumのモデルでは，候補のvyとvxから1つ，候補のyとxから1の状態が選ばれている．

SimulationCenterオプションで動的状態の変更についてのDebug Outputをオンにしてあると，シミュレーションのどこで状態が切り替わったかが分かる．メッセージはシミュレーションログのタブに出力される．10秒間のシミュレーション中にPendulumモデルに選択された状態が数回切り替わったことが分かる．

StateSelect属性

ある変数が静的状態として好ましいということを知っているならば，変数宣言の修飾子としてstateSelect=StateSelect.alwaysを加えることができる．こうすると，System Modeler がこの変数をチェックなしに静的状態として選ぶ．StateSelect.alwaysをあまり多くの変数に加えると，System Modeler がビルドログに警告を出力し，stateSelectの全設定を無視するかもしれないので注意が必要である．以下の「model ForceState」では，System Modeler は1つの状態を選択する必要があり，StateSelect.alwaysを使ってSystem Modeler にxを選択することが強制されている．

model ForceState
  Real x(stateSelect = StateSelect.always);
  Real y;
initial equation
  y = 1.0;
equation
  x - y = sin(time);
  der(x) + der(y) = 1.0;
end ForceState;

stateSelect=StateSelect.preferを加えてSystem Modeler にある変数が状態として好ましいというヒントを与えることもできる．こうすると動的状態候補の数を少なくすることもできる．動的状態選択を使っているモデルがあり，あまりに多くの候補からの選択が行われているなら，候補の変数にStateSelect.preferを設定して候補の数を減らすことができる．

Reinit演算子

When方程式の中でreinit演算子を使ってWhen条件が生起した場合に状態の値を変えることができる．簡単な例として以下の「model Sawtooth」をご覧いただきたい．再初期化される変数は状態でなければならないので，System Modeler はこの変数にStateSelect.alwaysを自動的に設定する．

model Sawtooth
  Real x;
initial equation
  x = 0.0;
equation
  der(x) = 1.0;
  when sample(1.0, 1.0) then
    reinit(x, 0.0);
  end when;
end Sawtooth;

イベント

シミュレーションの間に．例えば，if式のブール式の値が変わった場合に，イベントが生成される．イベントが起ると，ソルバは停止し，イベントの際の厳密な点を求めて反復を開始する．この反復には時間がかかることがあるので，これを可能な限り最小限にするよう試みるとよいだろう．

不要な反復を避ける方法の一つに，組込みの演算子noEventを使って，イベントの生成が不要であるというヒントをソルバに与える方法がある．この演算子は，イベントの間，式が連続的である場合にのみ使うことができる（必ずしも微分可能である必要はない）．

model EventTest
  Real x1;
  Real x2;
equation
  x1=if time<3 then time else 3 "Event generated at time=3";
  x2=noEvent(if time<3 then time else 3) "No event generated";
end EventTest;

noEvent演算子を使って不正評価を阻止することもできる．次の例では，sin(x)/xが計算されている．0による除算を阻止するために，abs(x) > 0の前後にnoEventが使われていて，x = 0の場合はsin (x)/xが評価されないようになっている．

model GuardEval
  Real x;
  Real y;
equation
  x=time - 1;
  y=if noEvent(abs(x) > 0) then sin(x)/x else 1;
end GuardEval;

多体ライブラリ(MultiBody Library)

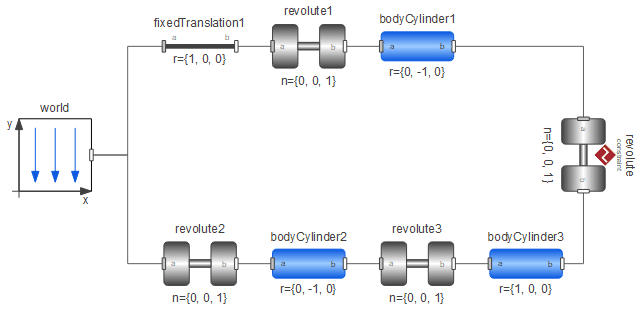
Modelica.MultiBodyは，3D力学モデリングのためのModelicaのライブラリである．3Dモデルでは，すべてのパーツを空間で接続せねばならず，システムが動き始めるためには初期値が正しくなければならないので，扱いには用心しなければならない．System Modeler には，MultiBodyライブラリを使って作られたモデルの可視化機能が備わっており，動きの分析が簡単にできるようになっている．以下は，MultiBodyライブラリを使う上で考慮すべき事柄である．ライブラリの紹介とコンポーネントについての情報は，Modelica.MultiBodyパッケージおよびそのクラスに埋め込まれたドキュメントを参照されたい．以下の図はMultiBodyライブラリを使った例を示している．

1.gif

平面ループの例

初期値

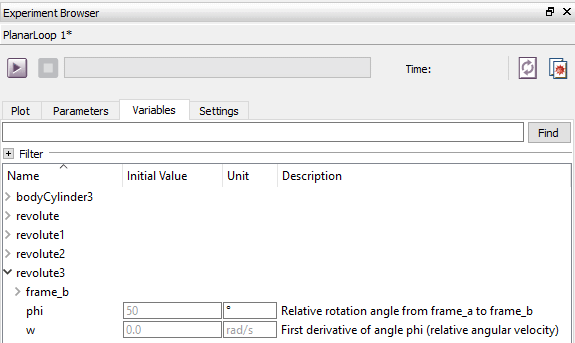
物理的に正しいモデルを得るためには，システムに状態を適切に初期化させることが重要である．この例では，revolute3中のパラメータstateSelectをStateSelect.alwaysに設定することで，revolute3コンポーネント中の状態を使うことにした．モデルが変換されたり構築されたりすると，適切な状態が選ばれる．これらの状態の初期値は，Simulation Centerの変数タブに示される．

2.gif

上ののスクリーンショットにおけるモデルの選ばれた状態

上記のスクリーンショットで分かるように，結合部revolute3の角度は速度0.0 rad/s，角度50度で始まる．値もまた，Model Centerの一般タブのモデル直接変えることができる．

オブジェクトの角度と位置

物理的に正確なモデルを得ることは重要である．さもなければシステムのシミュレーションは実行できないであろう．BodyCylinderやBodyBox等のコンポーネントには単純な方向，例えばr={1, 0, 0}，r={0, -1, 0}を使うとよい．他の方向が必要な場合は，結合部のphiを変えるか．あるいはMultiBody.Parts中のFixedRotationおよびFixedTranslationのコンポーネントを使う．

アニメーション

MultiBodyコンポーネントの中にはアニメーションの情報が入っているものがある．MultiBody.Parts中のBody，BodyBox，BodyCylinder，BodyShapeの各コンポーネントがそうである．MultiBody.Visualizersには速度，加速度等の特性を示す可視化機能もある．

3.gif

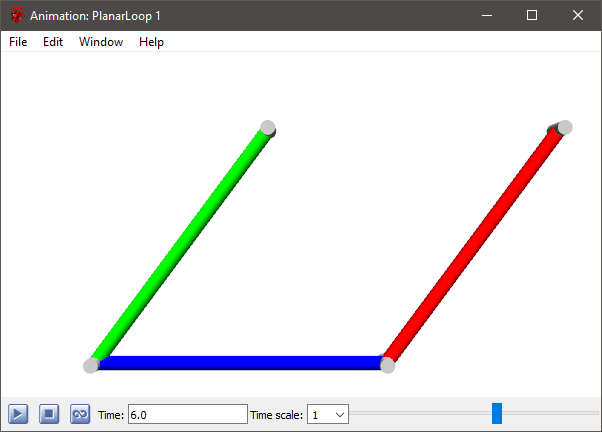
上記のモデルからの3本の棒を含む簡単なループモデルのアニメーション

それぞれの名前で示されているように，BodyBoxは箱形をしており，BodyCylinderは円柱形をしている．アニメーションのためにこれ以外の形（球，円錐，歯車等）が必要な場合は，BodyShapeを使い，パラメータshapeTypeを所望の形に設定するとよい．物理特性のない純粋なアニメーションが必要な場合は，Shapeオブジェクトを使うとよい．

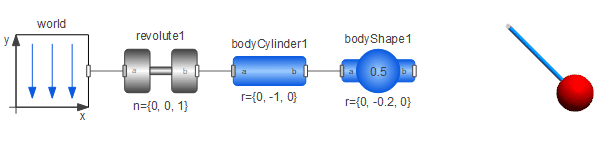
以下の図は，尖端に球の付いた振り子の例である．BodyShapeコンポーネントを使って球のアニメーションが行われている．振子モデルの可視化は，はるか右側まで見られる．

4.gif

尖端に球の付いた振り子モデル

CAD形状

CAD形状は，shapeTypeパラメータをCADファイルにアクセスするModelica URIに設定して指定することができる．Modelica URIは次のような構造になっている．

modelica://<Modelica-name>/<relative-file-path>

これは，Modelicaライブラリ<Modelica-name>の位置と相対的なパスを指定する．

System Modeler は，次のCAD形状形式をサポートする．

一般的な助言

以下は，よくある問題を回避するために役に立つ，一般的なヒントである．