Wolfram Language Home Page »

Troubleshooting Model Initialization

Following is a collection of short demonstrations of how to troubleshoot common problems in model initialization. See Model Initialization for background on the concepts involved.

Unexpected Initial Value

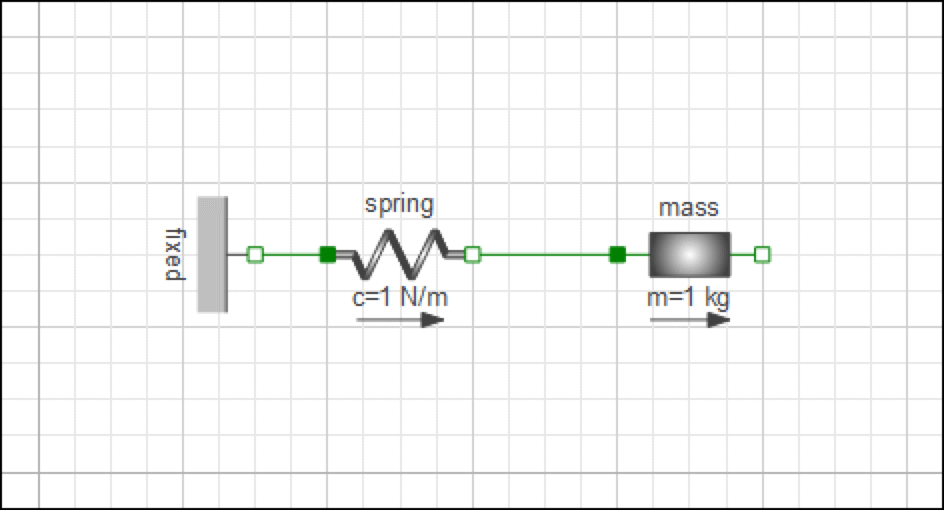
Sometimes, a model may initialize without any problems, except that it is not in the desired initial system state. It may then be necessary to figure out where in the initialization process the path taken by model initialization diverges from the expectations. This is illustrated by the following simple spring-mass system DocumentationExamples.Tutorial.SpringInitialization.Initialize_s_rel, where the goal is to initialize spring.s_rel to 5.

Diagram of a translational spring-mass system.

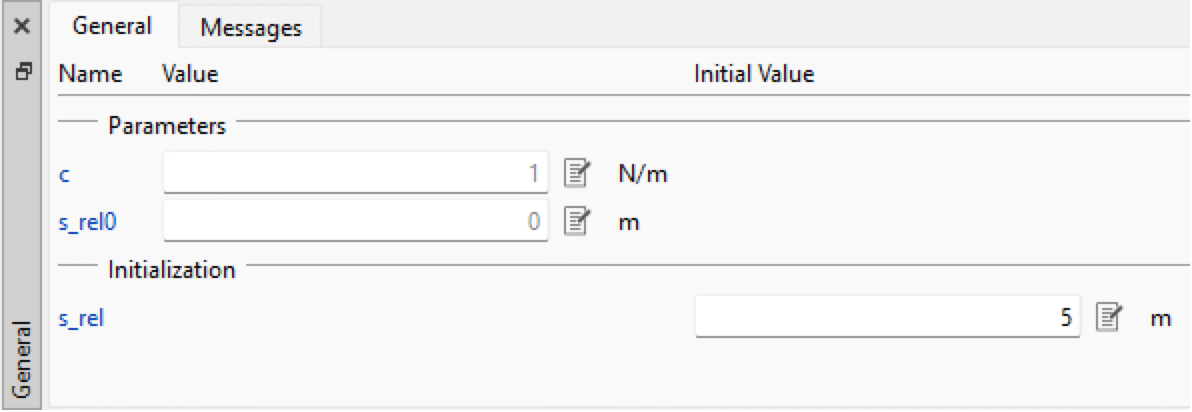
The initial (non-working) attempt at obtaining the desired initialization is to simply select the spring component and set the Initial Value for s_rel.

Setting the initial value for spring.s_rel to 5.

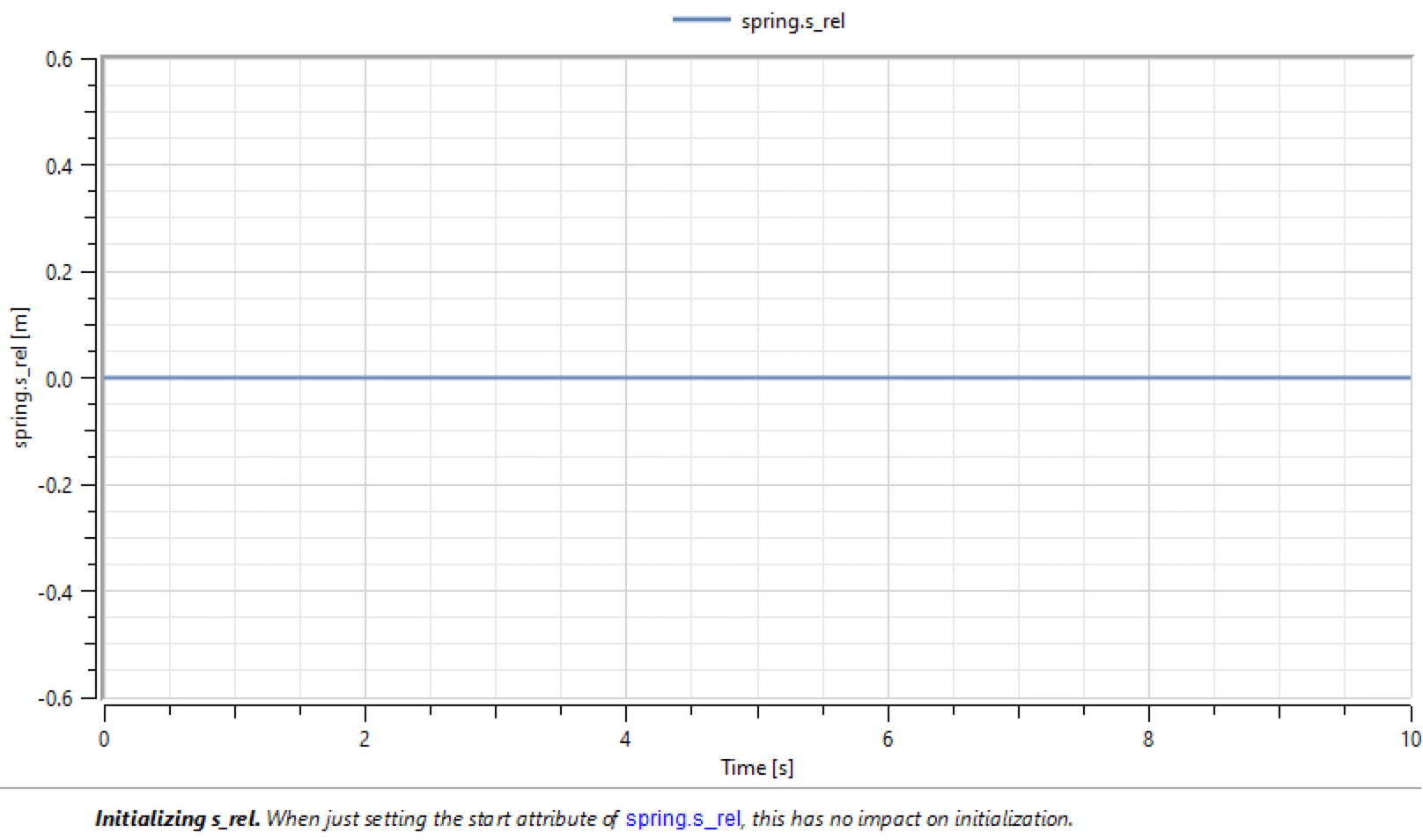
When the model is simulated, it is seen that the initialization has no effect.

Simulation result showing that spring.s_rel was initialized to 0.

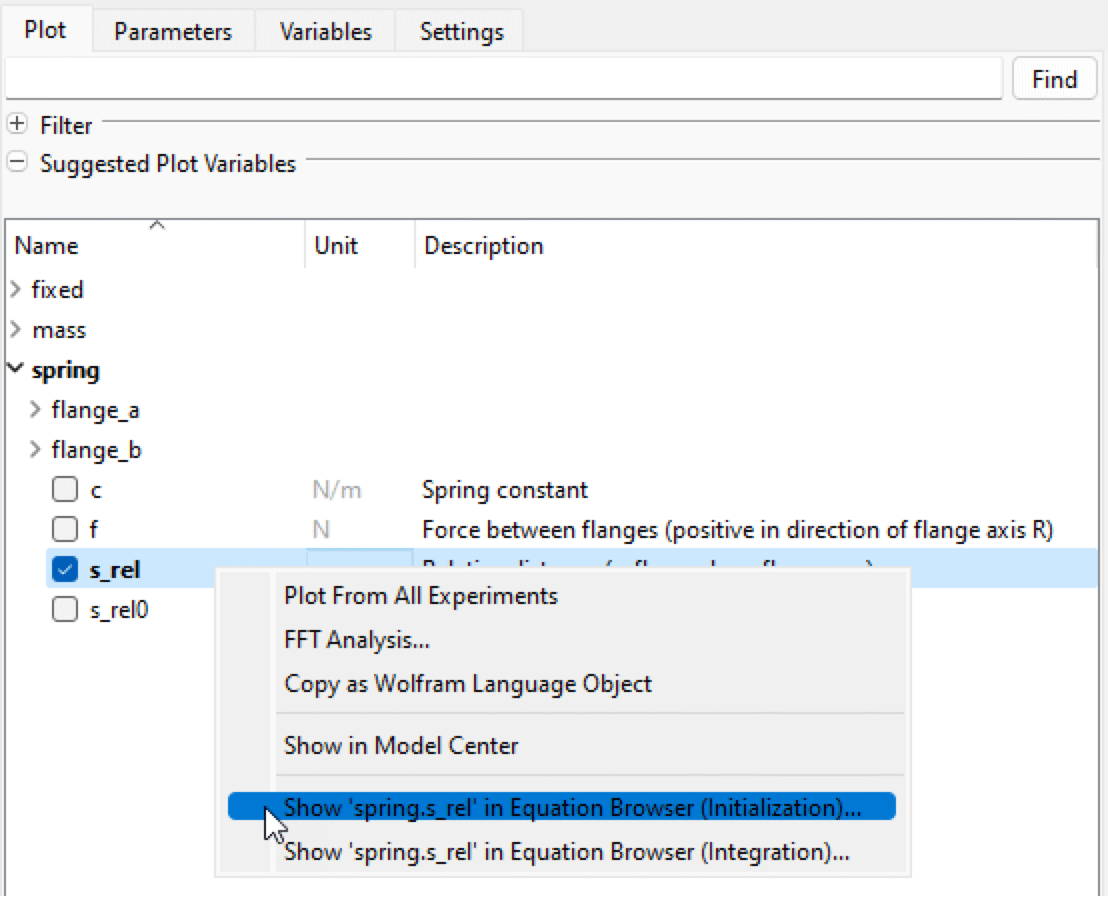
To really understand the problem before attempting to fix it, the Equation Browser can be used to trace the origin of the initial value of spring.r_rel. To get started, one can use the context menu for this variable in the Plot tab of the Experiment Browser.

Context menu for spring.s_rel in the Plot tab of the Experiment Browser.

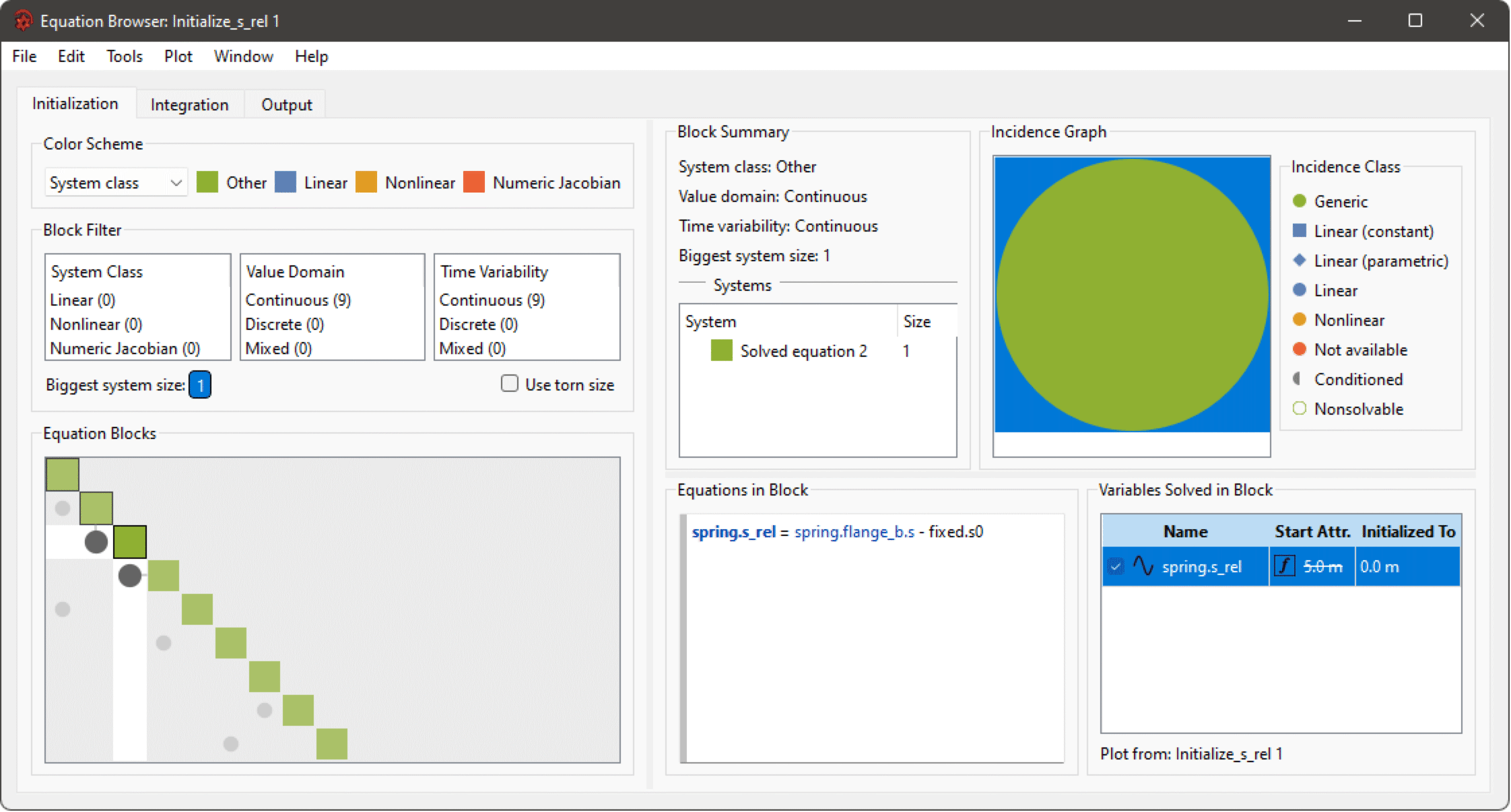
Select Show 'spring.s_rel' in Equation Browser (Initialization)…. The following view appears in the Equation Browser.

The Equation Browser showing the initialization of spring.s_rel.

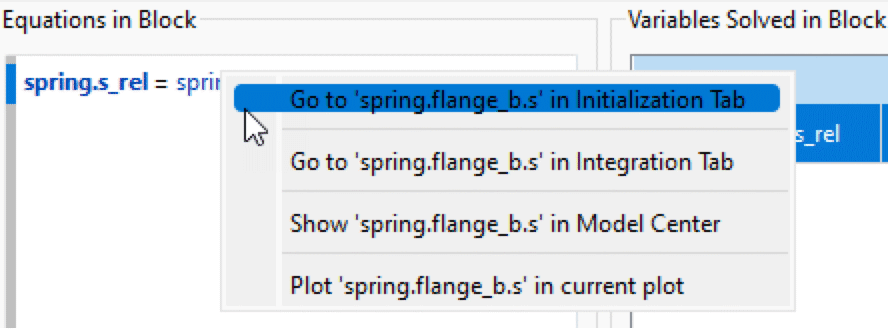
It can be seen that spring.s_rel is not initialized from its start attribute, but from an equation depending on spring.flange_b.s. Plotting the parameter fixed.s0 shows that its value is 0, meaning that the desired value spring.flange_b.s is 5. To find how spring.flange_b.s is initialized, left-click it in the equation and select Go to 'spring.flange_b.s' in Initialization Tab in the menu that pops up.

Using left-click context menu to go to the initialization of spring.flange_b.s.

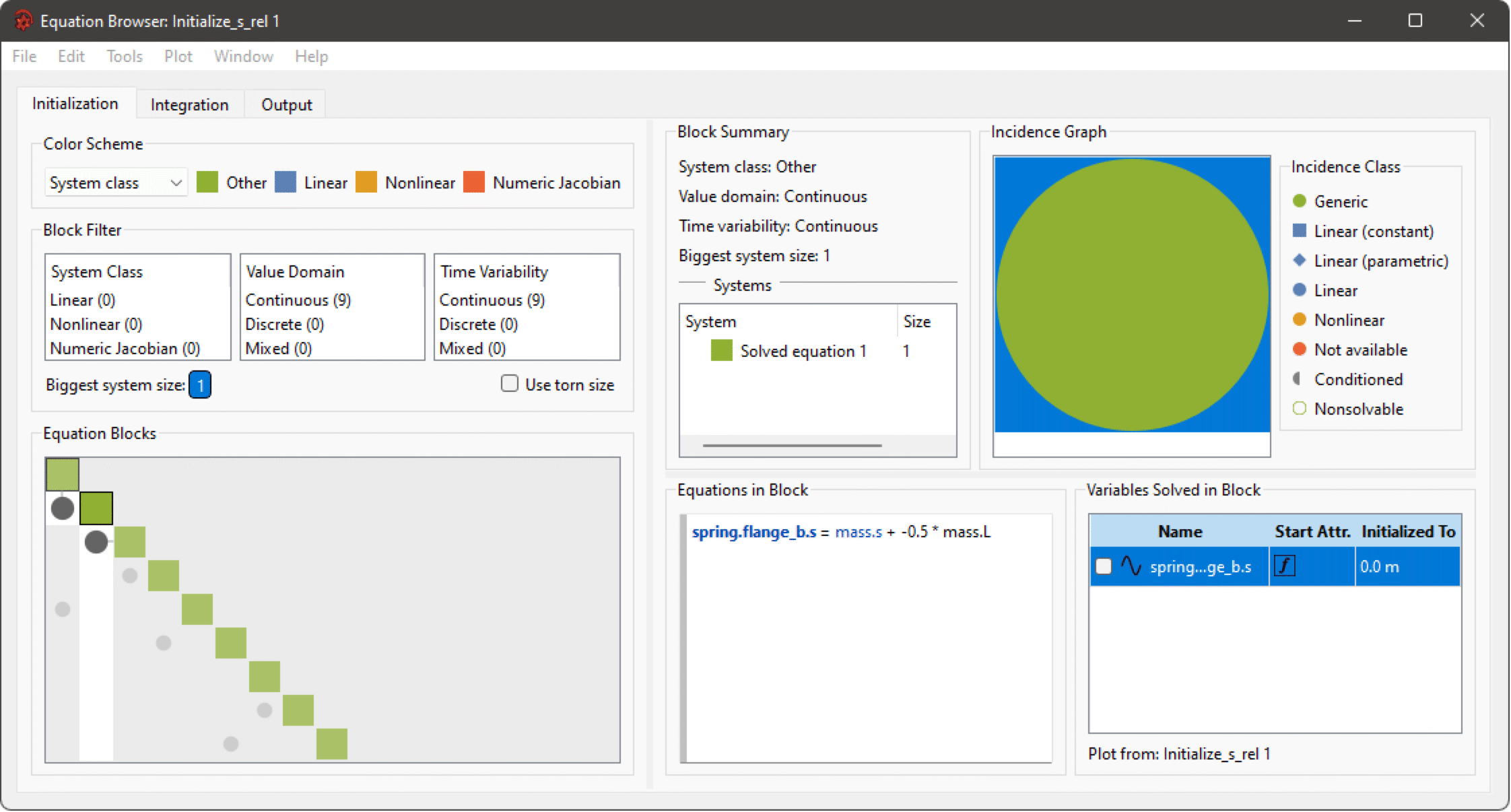
The Equation Browser then shows the following system.

The Equation Browser showing the initialization of spring.flange_b.s.

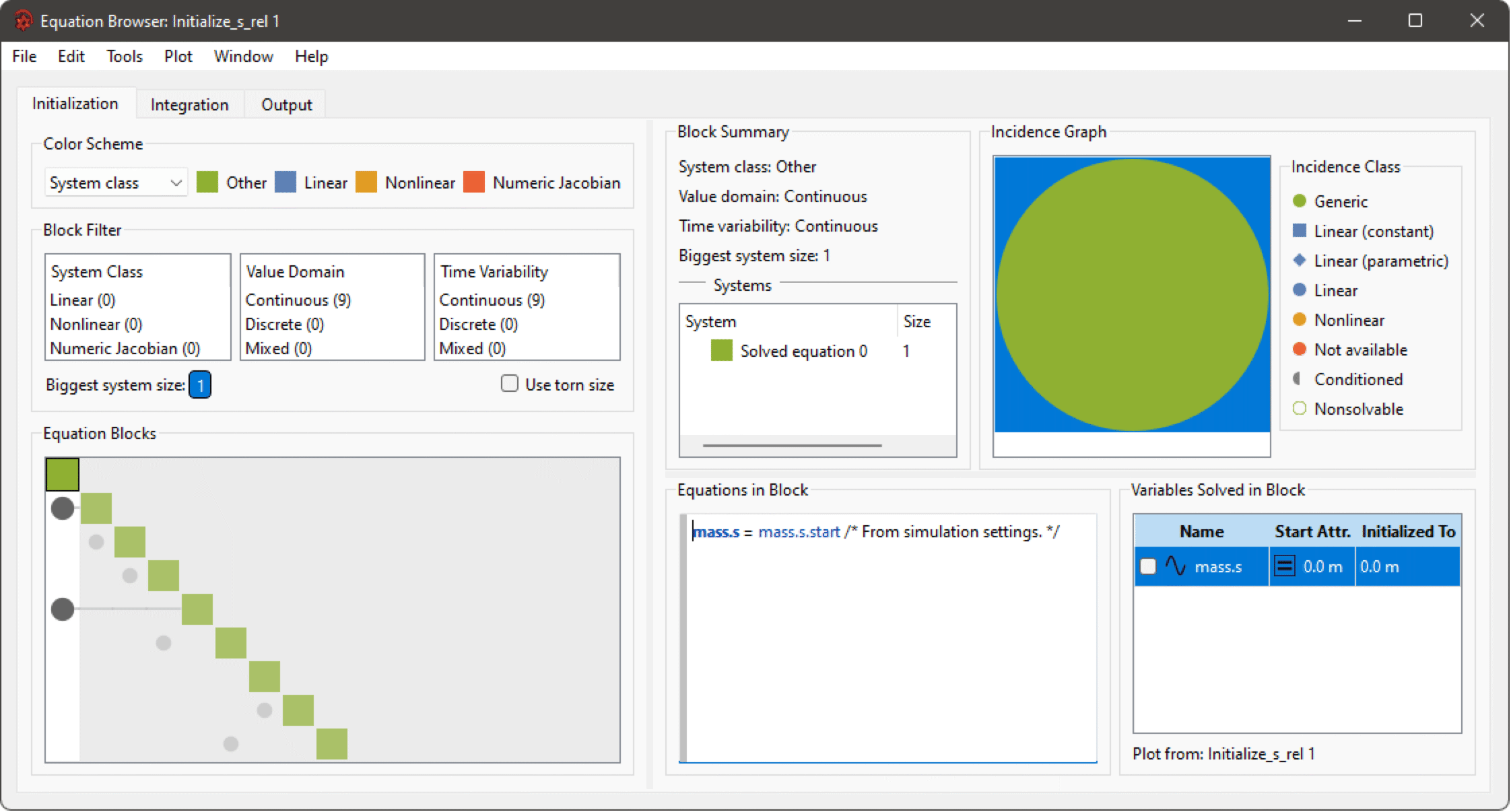
Plotting the parameter mass.L shows that it has a value of 0, meaning that the desired value of mass.s is 5. In the left-click menu for mass.s, Go to 'mass.s' in Initialization Tab finally leads to the following system.

The Equation Browser showing the initialization of mass.s.

It can now be seen that it is mass.s that is initialized from its start attribute, having a value of 0.0. The investigation has revealed that it—through a chain of other variables—then determines the initialization of spring.s_rel, overriding the desired value of 5.

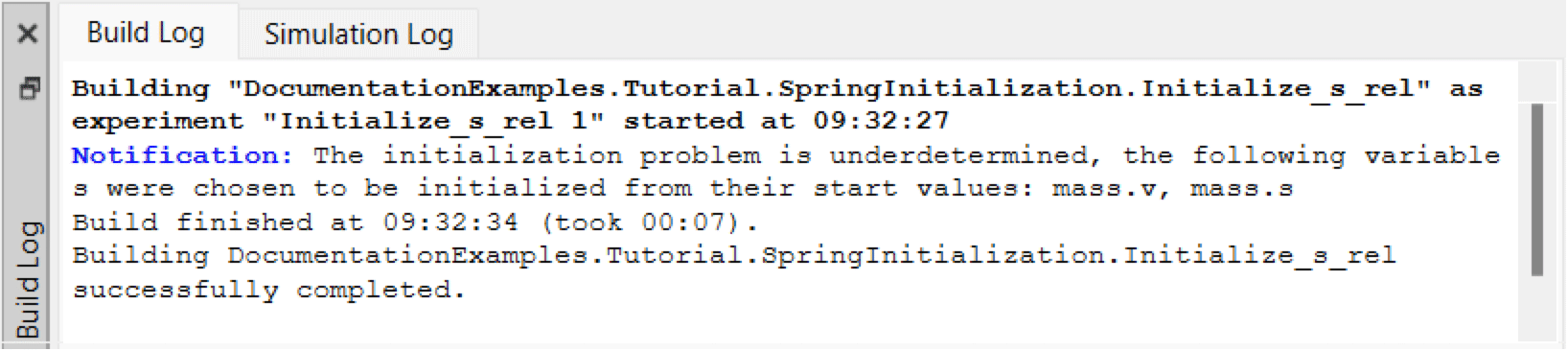
Having seen how to investigate this problem following the generic approach of tracing variable initialization in the Equation Browser, it should be mentioned that in this particular case it would have been sufficient to just read the build log notifications.

Build log notifications, including one regarding underdetermined initialization.

With only limited intuitive understanding of the spring-mass system, it can be realized that the notification saying that mass.s will be initialized from its start value means that the provided start attribute for spring.s_rel cannot be respected at the same time and will be ignored.

There are many ways in which the model can be fixed to get the desired initialization. Two ways are illustrated by DocumentationExamples.Tutorial.SpringInitialization.Initialize_s_rel_fixed and DocumentationExamples.Tutorial.SpringInitialization.Initialize_mass, and the reader is encouraged to simulate these and use the Equation Browser to see in which ways spring.s_rel is now getting the desired value.

Removing Underdetermined Initialization

The DocumentationExamples.Tutorial.MultiBody.TwoCylinders is a very simple multi-body model that fails to initialize.

Diagram of multi-body model with two connected cylinders.

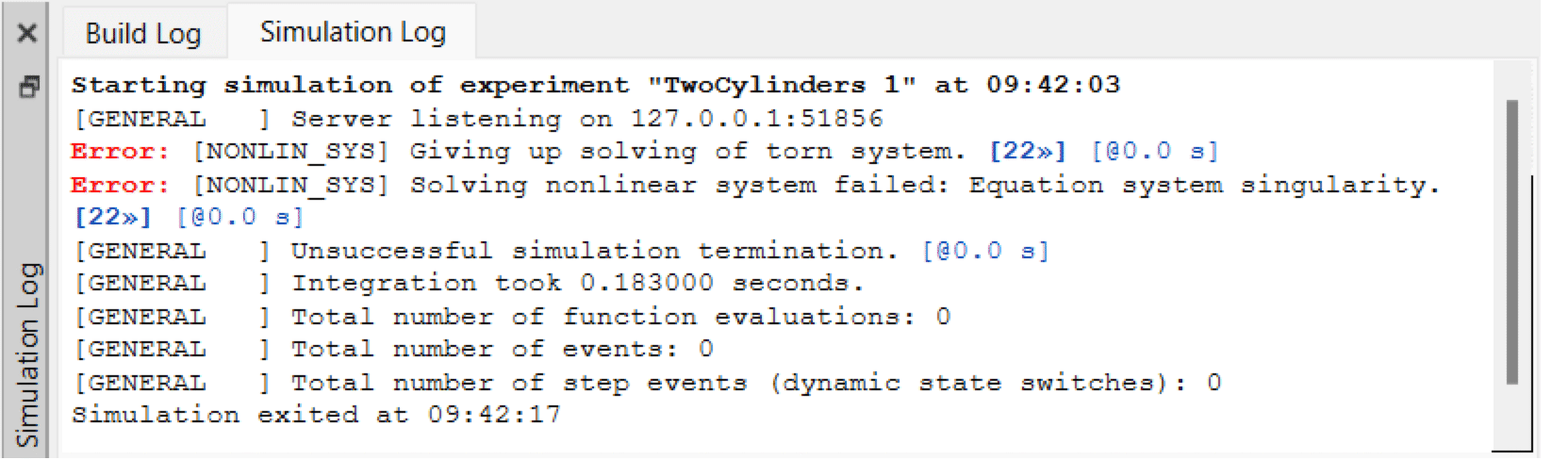
The simulation log shows that there is a problem with a nonlinear system of equations.

Simulation log showing failure to solve a nonlinear system during initialization.

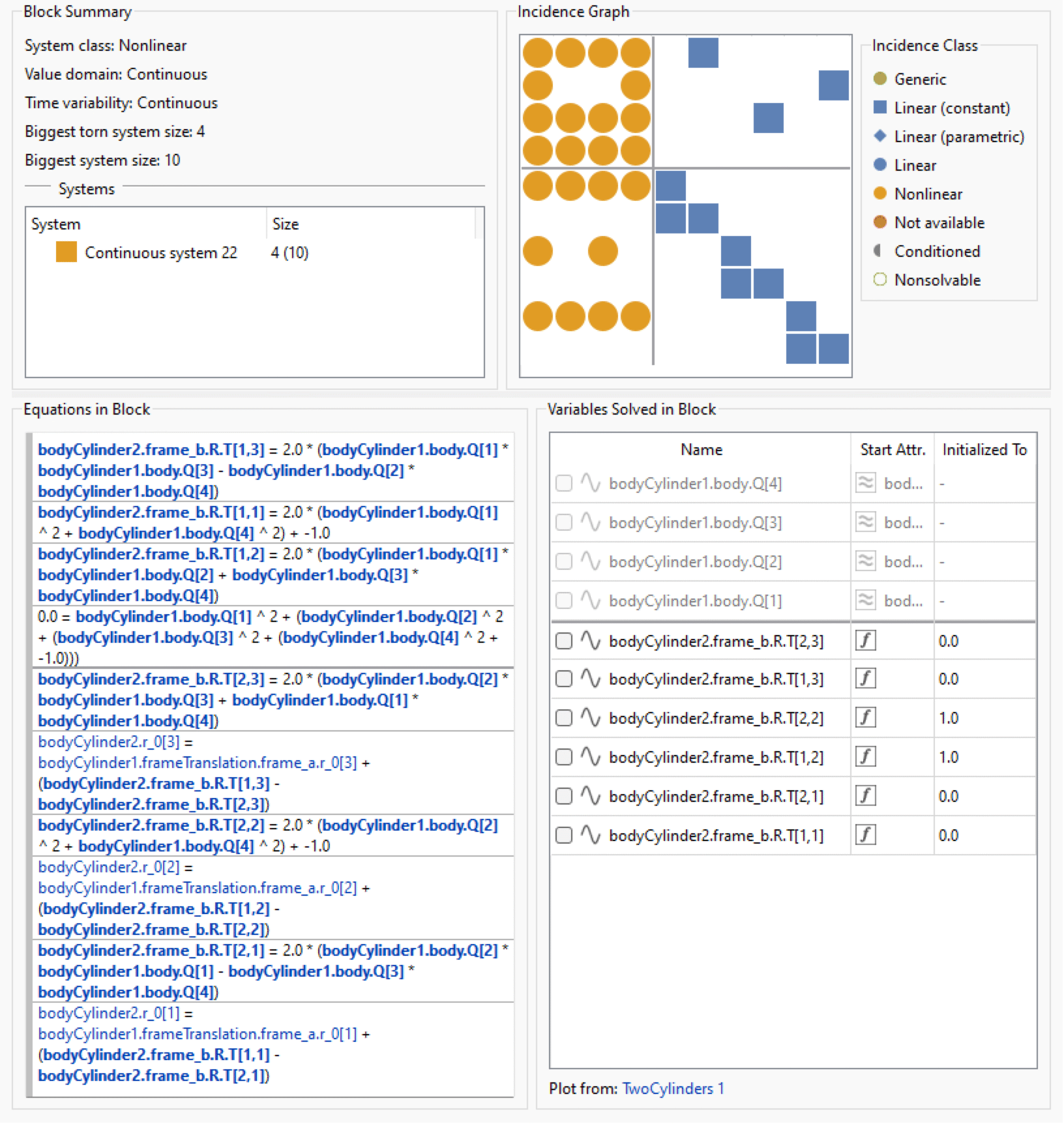
While it is generally a good idea to follow the equation system link into the Equation Browser, it is not easy in this case to see whether a solution to the nonlinear system even exists. What can be seen, however, is that the unknowns of this system are the unit quaternion components describing the orientation of bodyCylinder1.

Equation Browser view of the failing nonlinear equation system.

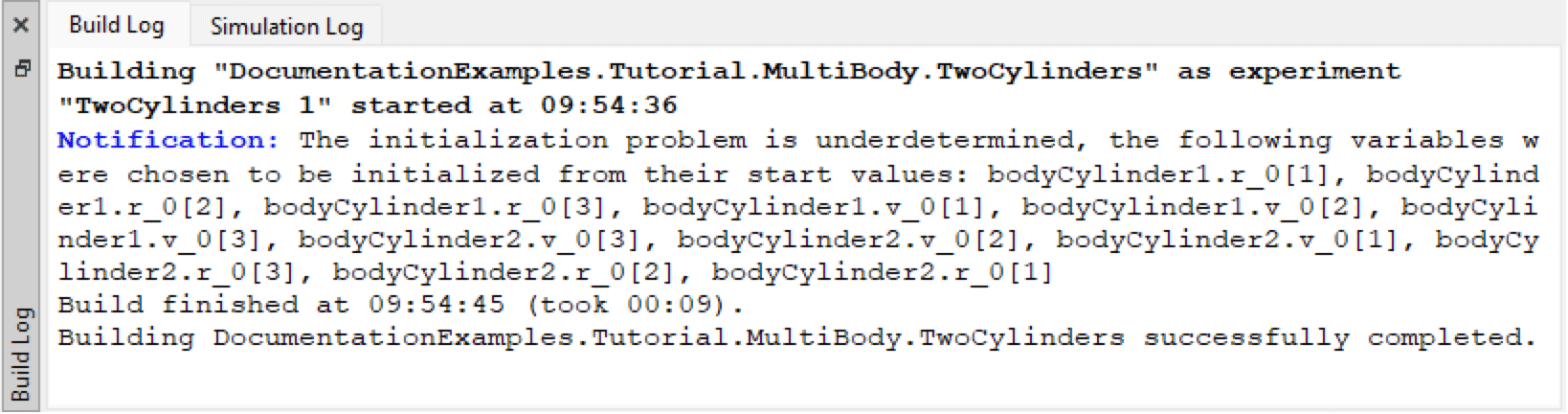
An experienced reader might note that solving this kind of nonlinear equation system for an orientation is unexpectedly complicated compared to what one would expect of two connected cylinders. A thorough reader who tried simulating the model may also have checked the build log and noted the following notification.

Build log notifications, including one regarding underdetermined initialization.

In particular, the notification is about the underdetermined initialization that turns out to be the key to fixing the initialization of this model. Understanding that bodycylinder1.r_0 and bodycylinder2.r_0 are the cylinder positions in space, it is now becoming clear why independently initializing these from start attributes and then trying to find a matching orientation is not going to work.

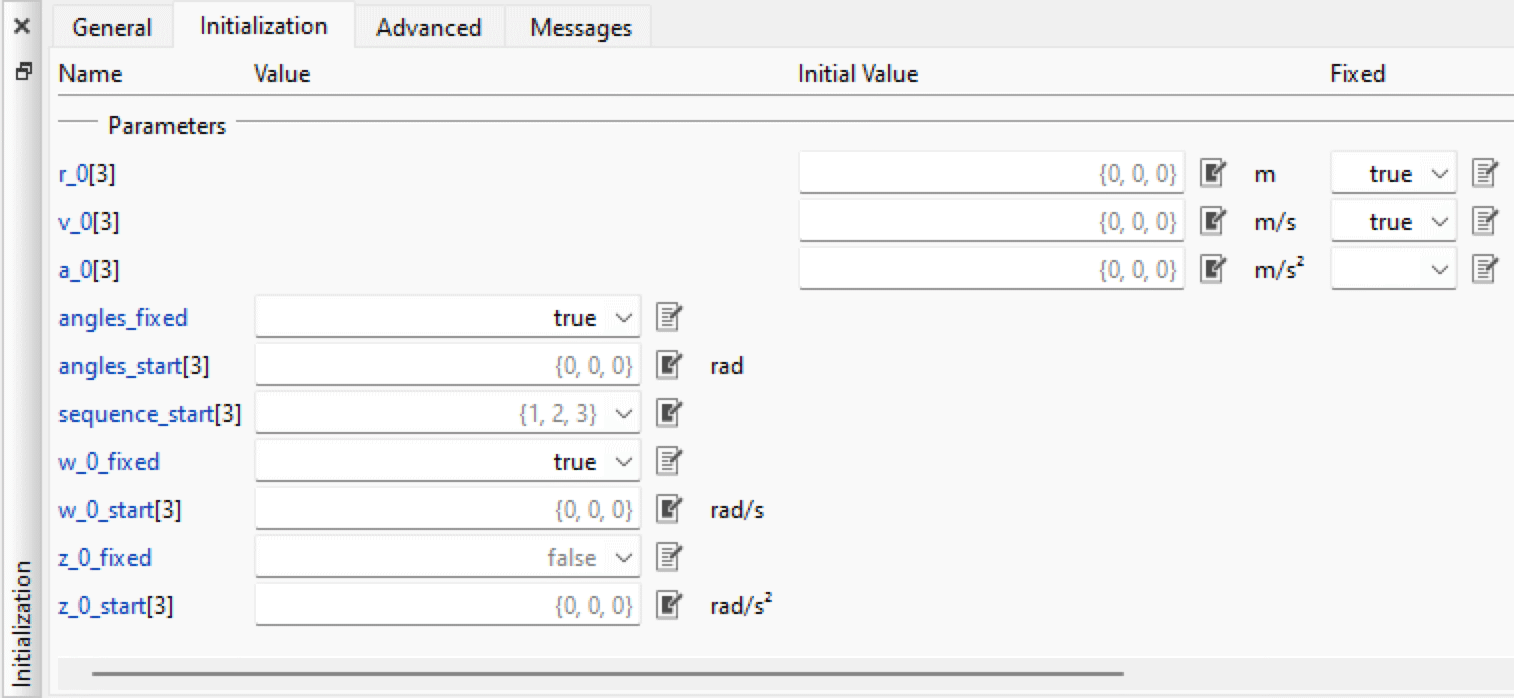
To solve the problem, one should take full control over the initialization so that there are no underdetermined parts. In Model Center, one can do that by—for example—using fixed initialization of position, velocity, orientation and angular velocity for bodycylinder1, as is done in DocumentationExamples.Tutorial.MultiBody.TwoCylindersFixed.

Editing the initialization of bodycylinder1 in Model Center.

Now, the build log notification about underdetermined initialization is gone, the simulation succeeds without any warnings in the simulation log, and the Equation Browser shows that the complicated nonlinear equation system in the initialization problem is replaced by a simpler one.