WOLFRAM SYSTEM MODELER
UserDefinedComponentsUser Defined Components |
|
Wolfram Language

SystemModel["Modelica.Mechanics.Translational.UsersGuide.UserDefinedComponents"]

Information
This information is part of the Modelica Standard Library maintained by the Modelica Association.
In this section some hints are given to define your own 1-dimensional translational components which are compatible with the elements of this package. It is convenient to define a new component by inheritance from one of the following base classes, which are defined in sublibrary Interfaces:
| Name | Description |
|---|---|
| PartialCompliant | Compliant connection of two translational 1-dim. flanges (used for force laws such as a spring or a damper). |
| PartialCompliantWithRelativeStates | Same as "PartialCompliant", but relative position and relative speed are defined as preferred states. Use this partial model if the force law needs anyway the relative speed. The advantage is that it is usually better to use relative positions between drive train components as states, especially, if the position is not limited. |
| PartialElementaryTwoFlangesAndSupport2 | Partial model for a 1-dim. translational component consisting of the flange of an input shaft, the flange of an output shaft and the support. |
| PartialForce | Partial model of an external force acting at the flange (accelerates the flange). |
| PartialTwoFlanges | General connection of two translational 1-dim. flanges. |
| PartialAbsoluteSensor | Measure absolute flange variables. |
| PartialRelativeSensor | Measure relative flange variables. |
The difference between these base classes are the auxiliary variables defined in the model and the relations between the flange variables already defined in the base class. For example, in model PartialCompliant there is no support flange, whereas in model PartialElementaryTwoFlangesAndSupport2 there is a support flange.
The equations of a mechanical component are vector equations, i.e., they need to be expressed in a common coordinate system. Therefore, a local axis of movement has to be defined for a component. All vector quantities, such as cut-forces or velocities have to be expressed according to this definition. Examples for such a definition are given in the following figure for a mass component:
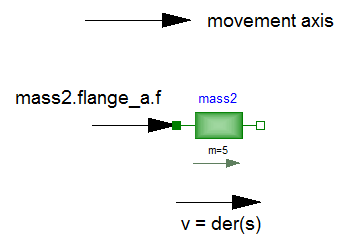
As can be seen, all vectors are directed into the direction of the movement axis. The positions in the flanges are defined correspondingly.
On first view, one may assume that the selected local coordinate system has an influence on the usage of the component. But this is not the case, as shown in the next figure:
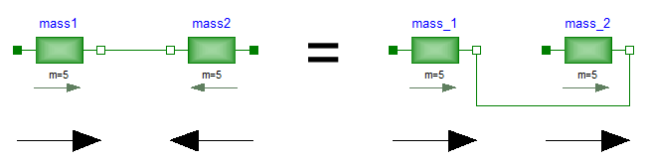
In the figure, the local axes of translation of the components
are shown. The connection of two masses in the left and in the
right part of the figure are completely equivalent, i.e., the right
part is just a different drawing of the left part. This is due to the
fact, that by a connection, the two local coordinate systems are
made identical and the (automatically) generated connection equations
(= positions are identical, cut-forces sum-up to zero) are also
expressed in this common coordinate system. Therefore, even if in
the left figure it seems to be that the velocity vector of
mass2 goes from right to left, in reality it goes from
left to right as shown in the right part of the figure, where the
local coordinate systems are drawn such that they are aligned.
Note, that the simple rule stated in section
Sign conventions
also determines that
the velocity of mass2 in the left part of the
figure is directed from left to right.
To summarize, the local coordinate system selected for a component is just necessary in order that the equations of this component are expressed correctly. The selection of the coordinate system is arbitrary and has no influence on the usage of the component. Especially, the actual direction of, e.g., a cut-force is most easily determined by the rule of section Sign conventions. A more strict determination by aligning coordinate systems and then using the vector direction of the local coordinate systems, often requires a re-drawing of the diagram and is therefore less convenient to use.
