5. Multistage Mechanisms

Overview

This chapter covers one of the more advanced methods of kinematic modeling supported by MechanicalSystems. Stage switches and time switches are Mech's method of allowing a mechanism to jump from one constraint type to another as it moves through its range of motion. These functions enable the modeling of components such as a pin that slides in a track with a sharp jog in it, or a bumper that swings through an arc until it strikes a stationary pad and starts it in motion. Mech also supports multistage load functions, which are covered in Chapter 7.

5.1 Stage Switching Constraints

A StageSwitch constraint is nothing more than a compound constraint that contains several normal Mech constraints and lets the user specify which one is active. This function can be used to model any mechanism that has more than one mode of operation, and it is desired to automatically switch the model from one mode to another.

5.1.1 StageSwitch

A multistage mechanism constraint-switching function.

A StageSwitch constraint returns an error if any of the test expressions fail to return either True or False at runtime. Because StageSwitch does evaluate its own arguments immediately, unlike Which or If, test expressions such as SameQ should not be used. This is because SameQ evaluates immediately to True or False instead of waiting until some future condition changes. Also, a StageSwitch constraint is invalid if all of the test expressions return False at runtime because no constraint is applied to the model.
Each of the constraints supplied to the StageSwitch constraint are standard Mech constraint objects or lists of constraint objects. Each constraint or list of constraints must constrain the same number of degrees of freedom. Note that the constraint numbers of the constraints that are inside of the StageSwitch constraint are irrelevant. The constraint number of the entire StageSwitch constraint is the only one that is used to reference the constraint.

Examples

This loads the Modeler2D package.

In[1]:=

The following example shows how StageSwitch (constraint 1) might be used to model a pin on a slider that slides in one of two straight tracks on the ground body. Which track to use is determined by the value of the user-defined symbol whichtrack, which must be either 1 or 2.

Here is a valid StageSwitch constraint.

In[2]:=

Out[4]=

The following example shows how a StageSwitch constraint that constrains two degrees of freedom might be implemented. The first constraint in the StageSwitch constraint forces the origin of the slider to be coincident with the origin of the ground. If the value of the user-defined symbol pressure rises above 100 units, the second constraint pair becomes active and forces the origin of the slider to lie upon a line and be positioned as a function of the value of pressure.

Here is a valid StageSwitch constraint.

In[5]:=

Out[5]=

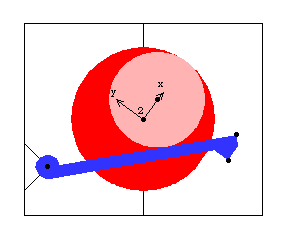
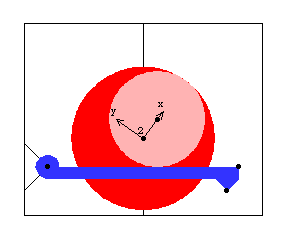
5.1.2 Rocker Example Mechanism

To demonstrate the use of the Modeler2D StageSwitch function, a 2D model of a rocker arm driven by an eccentric is developed. The model consists of two moving bodies, the eccentric and the rocker.
This mechanism has two distinct modes of operation that are toggled via the StageSwitch function. The first mode of operation is for the eccentric to be rotated about a stationary axis, forcing the rocker to reciprocate by its contact with the eccentric. The second mode is for the eccentric to be rotated about an axis that is unconstrained in the vertical direction while the rocker is constrained to be stationary. This causes the eccentric to rise and fall as a result of its rotation.

Here is the 2D rocker model graphic.

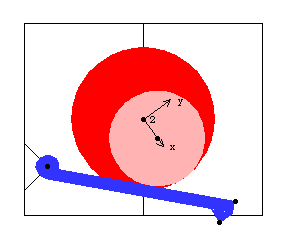
Bodies

Three bodies are used in the rocker mechanism model.

Here are all of the bodies in the rocker model.

Names are defined for each of the body numbers in the model.

In[6]:=

SetBodies is used only to set a nonzero initial guess for the rocker.

In[9]:=

Constraints

Four regular constraints and one StageSwitch constraint are used to model the rocker mechanism.

A StageSwitch constraint with two stages constrains the remaining one degree of freedom. Which mode of operation is active is determined by the boolean value of rockerfree.
If rockerfree is True, a RelativeY1 constraint specifies the Y coordinate of the axis of the eccentric, leaving the rocker free to reciprocate.
If rockerfree is False, a RotationLock1 constraint enforces that the rocker does not rotate, leaving the eccentric free to reciprocate vertically.

Here is the complete rocker mechanism, built in one step.

In[10]:=

Runtime

The rocker mechanism model is first run with rockerfree set to True. This enables the first stage of the StageSwitch constraint.

The model is first run at T = 0.15 with the rocker free to rotate.

In[12]:=

Out[13]=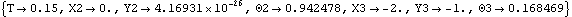

Here is the rocker mechanism with rockerfree = True.

Now the mechanism model is run with rockerfree set to False. This enables the second stage of the StageSwitch constraint.

The model is now run at T = 0.15 with the rocker fixed.

In[14]:=

Out[15]=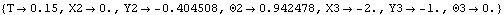

Here is the rocker mechanism with rockerfree = False.

Undocumented Graphics Generation

The following inputs generate the graphics in this section. These Modeler2D commands are defined in Chapter 3.

In[39]:=

In[41]:=

In[42]:=

In[43]:=

In[44]:=

In[45]:=

In[46]:=

In[47]:=

In[48]:=

In[49]:=

In[56]:=

In[58]:=

In[59]:=

In[60]:=

In[62]:=

In[63]:=

In[65]:=

5.1.3 Slider-Ramp Example Mechanism

Another usage of the StageSwitch constraint is to switch from one stage of operation to another when such switching is the normal progression of operation of the mechanism. To demonstrate this usage a 2D model of a slider on a ramp is developed. The model has only one moving body, the slider.
This mechanism has two distinct modes of operation. First, the slider travels across a horizontal surface until it encounters an inclined ramp. As the slider progresses further, its front edge leaves the horizontal plane and begins to slide up the inclined ramp. StageSwitch is used to switch between these modes by defining the test expressions in the StageSwitch constraint to test explicitly whether or not the corner of the slider has traveled beyond the bottom of the ramp.

Here is a graphic of the 2D slider-ramp model.

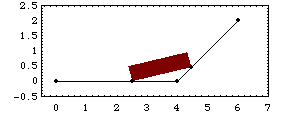
Bodies

Two bodies are needed in the slider-ramp mechanism model.

Here are both the bodies in the slider-ramp model.

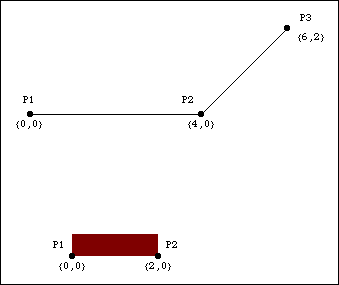
Names are defined for each of the body numbers in the model.

In[16]:=

Constraints

Two regular constraints and one StageSwitch constraint are used to model the slider-ramp mechanism.

A StageSwitch constraint with two stages eliminates the one remaining degree of freedom:
A PointOnLine1 constraint is used to place the right bottom corner of the slider on the horizontal surface if it is still to the left of the ramp.
A PointOnLine1 constraint is used to place the right bottom corner of the slider on the inclined ramp if it has passed to the right of the ramp.

Which stage of operation is active is determined by the value of a test expression that is a function of Modeler2D dependent variables. The test expression measures whether or not the right bottom corner of the slider has progressed far enough to the right to be on the inclined ramp.

Here is the slider-ramp mechanism built in one step.

In[18]:=

Runtime

The slider-ramp mechanism model can be run at any time, T, up to T = 4 with valid results. After T = 4, the left bottom corner of the slider passes the inclined ramp, but it does not travel up the ramp because the constraints have not been written to accommodate this.

This runs the model at T = 1.

In[19]:=

Out[19]=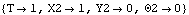

The slider-ramp mechanism is still on the horizontal segment of the ramp.

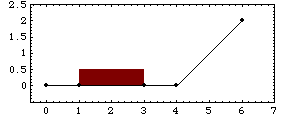
Now the model is run at T = 2.5, which puts the slider part way up the ramp.

In[20]:=

Out[20]=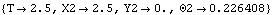

Here is the result.

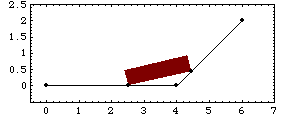
Undocumented Graphics Generation

The following inputs generate the graphics in this section. These Modeler2D commands are defined in Chapter 3.

In[93]:=

In[94]:=

In[95]:=

In[103]:=

In[97]:=

In[98]:=

In[105]:=

In[106]:=

In[107]:=

In[109]:=

5.2 Time Switching Constraints

A TimeSwitch constraint is a compound constraint that contains several normal Mech constraints and determines which one is active by the value of time T. This function can be used to model any mechanism that switches from one mode of operation to another with the progression of time.
A TimeSwitch constraint is basically a special case of a StageSwitch constraint that has switching capability explicitly dependent on time. All of the functionality of TimeSwitch can be duplicated with StageSwitch, except that the TimeSwitch constraint can be used with another special function, FindSwitchTime, that is used to seek the point in time at which two adjacent constraints should switch from one to the next.

5.2.1 TimeSwitch

The time-dependent, stage-switching function.

Each of the constraints supplied to the TimeSwitch must be a Mech constraint object, or a list of constraint objects. Each constraint or list of constraints must constrain the same number of degrees of freedom. Note that the constraint numbers of the constraints that are inside of the TimeSwitch are irrelevant. The constraint number of the entire TimeSwitch is the only one used to reference the entire constraint.

Examples

This loads the Modeler2D package.

In[1]:=

The following example shows how a TimeSwitch constraint (constraint 1) might be used to model a pin on a slider that slides along a horizontal track on the ground until the value of time reaches 2.0, at which time the pin begins to slide up an inclined track.
This constraint could replace the StageSwitch constraint used in the slider-ramp model in Section 5.1.

Here is a valid TimeSwitch constraint.

In[2]:=

Out[4]=

The following example shows how a TimeSwitch constraint that constrains two degrees of freedom might be implemented. The first constraint in the TimeSwitch constraint forces the origin of the slider to be coincident with the origin of the ground. If the value of time rises above 4.0, the second constraint pair becomes active, which forces the origin of the slider to lie upon an inclined line, while the Y coordinate of the origin of the slider is a function of time.

Here is a valid TimeSwitch constraint.

In[5]:=

Out[5]=

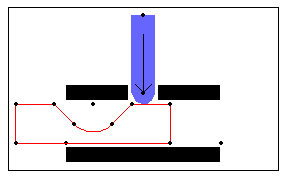
5.2.2 Detent Mechanism Example

To demonstrate the use of the Modeler2D TimeSwitch function a 2D model of a detent mechanism is developed. The model consists of two moving bodies, a slider and a detent plunger.
The detent mechanism goes through seven distinct stages of operation as the detenter passes across the slider, down into the detent notch, and back out. These stages are progressively activated via the TimeSwitch function as follows.

In stage 1 the detenter travels across the right top surface of the slider.
In stage 2 the detenter travels around the corner that leads into the detent notch.
In stage 3 the detenter travels down the inclined right side of the detent notch.
In stage 4 the detenter travels around the round bottom of the detent notch.
In stage 5 the detenter travels up the inclined left side of the detent notch.
In stage 6 the detenter travels around the corner that leads out of the detent notch.
In stage 7 the detenter travels across the left top surface of the slider.

Here is the 2D detent model graphic.

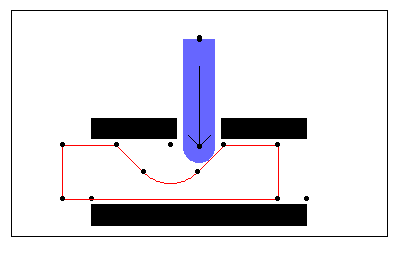
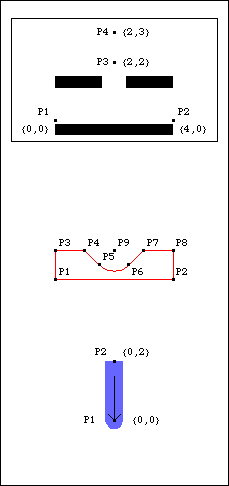
Bodies

Three body objects are defined for the detent mechanism model.

Names for each body number in the model are defined.

In[6]:=

In[9]:=

In[10]:=

In[11]:=

Here are all three bodies in the detent mechanism model.

The body objects are incorporated into the model.

In[12]:=

Constraints

Three regular constraints and one TimeSwitch constraint are used to model the detent mechanism.

The TimeSwitch constrains the one remaining degree of freedom:
Four of the seven stages of operation (1, 3, 5, and 7) are modeled by PointOnLine1 constraints that place the center of the detenter tip a specified distance (detenter tip radius) away from various lines on the slider.
The second and sixth stages, in which the detenter tip moves around sharp corners on the slider, are modeled with RelativeDistance1 constraints that place the center of the detenter tip a specified distance (detenter tip radius) away from the sharp corners on the slider.
The fourth stage, in which the detenter tip is traveling around the arc at the bottom of the detent notch, is also modeled with a RelativeDistance1 constraint that places the center of the detenter tip a specified distance (detent notch radius minus detenter tip radius) away from the center point of the arc.

The exact values of the switch times given as arguments to the TimeSwitch constraint are not known. The symbols given in place of switch times (tm2, tm3, etc.) are set to approximate values before running the model. The exact switch times will be determined later with FindSwitchTime.

Here are the three regular constraints.

In[13]:=

Here is the seven-stage TimeSwitch constraint.

In[17]:=

The constraints are incorporated into the current model.

In[18]:=

Runtime

Before the detent model can be run, the switch times used in the TimeSwitch constraint (tm2, tm3, etc.) must be given numeric values.

Here are guesses for switch times.

In[19]:=

Now the model is run at T = - 1.3.

In[23]:=

Out[23]=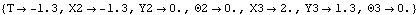

Here is the detent mechanism at T = - 1.3.

Now the model is run twice more at T = - 0.5 and T = - 0.1.

In[24]:=

Out[24]=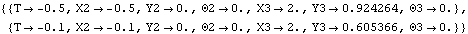

Here is the detent mechanism at the two new solution points.

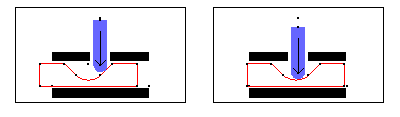
Note again that the current values of the switch times (tm2, tm3, etc.) are merely guesses. If the model is run at values very close to those times, incorrect results will be generated whenever the model uses the wrong constraint. The exact values of the switch times are found in Section 5.2.3 with the FindSwitchTime function.

5.2.3 Finding Switch Times

The Mech FindSwitchTime function is used to seek the time at which two adjacent constraints in a TimeSwitch are simultaneously valid, that is, to numerically find the correct switch time.

A function for seeking stage transition times.

FindSwitchTime works by adding one degree of freedom to the model (T becomes a dependent variable) and adding one extra constraint by using the pair of adjacent constraints simultaneously. FindSwitchTime uses the same solution block as SolveMech so it uses the most recent solution returned by SolveMech (LastSolve[]) for its initial guess.
FindSwitchTime accepts two options to deal with special situations that may arise in a pair of adjacent constraints, TangentConstraint and RequiredEquations.

Options for FindSwitchTime.

To understand the need for the RequiredEquations option, imagine a two degree of freedom TimeSwitch. If both sides of the adjacent two degree of freedom constraint pair are used simultaneously, two extra constraints are added to the model, but only one degree of freedom (time) is added. This results in an overconstrained model to which no solution can be found.
The default setting RequiredEquations -> {All, Sum} deals with this problem in a general but unsophisticated manner. All of the constraint equations from the first side of the TimeSwitch pair are used, as well as a single equation formed from the sum of all the equations from the second side, resulting in the required one extra constraint equation. This combination of constraints is valid if all of the equations in the second side of the constraint pair except one are redundant with respect to the equations in the first side. Thus the redundant equations in the sum are satisfied because of the first side of the constraint pair, and the one nonredundant equation is satisfied by the satisfying the sum. However, if there is no redundancy in the pair this will not work, and the solution will fail. If the default setting fails, the user must explicitly specify which equations to use to seek the switch time.
For example, take the following TimeSwitch example that was given in the beginning of this section.

Here is a TimeSwitch example.

In[25]:=

To seek the correct value of the switch time, which is currently set to 3.5, the following FindSwitchTime example could be used with all of the default option settings. Note that the TimeSwitch constraint is constraint number 3.

Here is a command to find the correct value of the switch time.

The default setting for RequiredEquations works fine in this case because the first constraint equation in the second side of the TimeSwitch constraint (PointOnLine1) is redundant with the first side of the TimeSwitch constraint (Revolute2), because PointOnLine1 must be satisfied for Revolute2 to be satisfied.
The following example shows a setting for RequiredEquations that explicitly specifies which equations to use. This setting would cause only the RelativeY1 constraint to be used from the second side of the TimeSwitch constraint.

Here is a setting of the RequiredEquations option.

When the RequiredEquations option is used with a TimeSwitch that contains multiple degree of freedom constraint functions, such as Revolute2 (2D) or Cylindrical4 (3D), it is necessary to know exactly what each of the 2, 3, 4, or 5 equations in the constraint are doing, so that you can know which ones need to be specified with the RequiredEquations option. To find out "which equation does what", see the notes on the particular constraint function in the appendix.

Detent Mechanism Example

In the detent mechanism example in Section 5.2.2, the values given for the switch times that were assigned variable names (tm2 = - 0.8, tm3 = - 0.4, etc.) were merely guesses. FindSwitchTime is used to find the correct values of the switch times.
The first and sixth switch times were set to values of - 1 and 1, respectively, which are exact values evident from the geometry of the detenter and notch.
The value of the second switch time must be found with FindSwitchTime. This is the time at which the detenter stops traveling around the sharp corner on the upper-right side of the detent notch and passes onto the inclined right side of the notch. These two adjacent constraints come into conjunction tangentially because there is no velocity discontinuity as the detenter passes onto the inclined flat side of the detent notch. Thus, FindSwitchTime must actually search for the point of tangency. This requires that the option TangentConstraint -> True be specified. Before FindSwitchTime is invoked, SolveMech is used to move the mechanism close to the correct position to provide better initial guesses.

This finds switch time 2 in constraint 4.

In[26]:=

Out[27]=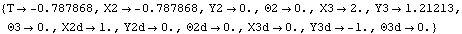

This sets the value of tm2.

In[28]:=

Out[28]=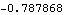

Here is the detent mechanism at the tangency point associated with tm2.

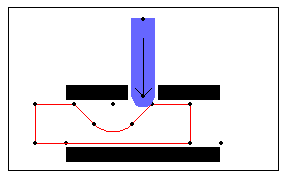
The third switch point occurs when the detenter passes from the inclined right side of the detent notch onto the round bottom of the notch. This is also a tangent constraint pair, so TangentConstraint -> True is used again.

This finds and sets switch time 3 in constraint 4.

In[29]:=

Out[29]=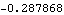

Here is the detent mechanism at the tangency point associated with tm3.

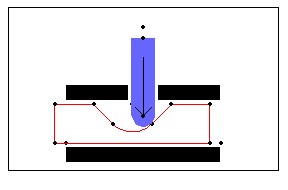
Because of symmetry, the values of tm4 and tm5 are known to be the negatives of tm3 and tm2, respectively. With all of the switch times set to valid values, the detent mechanism model can be run at any value of time.

Set the last two switch times.

In[30]:=

Undocumented Graphics Generation

The following inputs generate the graphics in this section. These Modeler2D commands are defined in Chapter 3.

In[242]:=

In[243]:=

In[244]:=

In[245]:=

In[246]:=

In[247]:=

In[248]:=

In[249]:=

In[250]:=

In[251]:=

In[252]:=

In[253]:=

In[254]:=

In[255]:=

In[256]:=

In[257]:=

In[258]:=