AsymptoticGreater[f,g,xx*]
gives conditions for ![]() or
or ![]() as xx*.
as xx*.
AsymptoticGreater[f,g,{x1,…,xn}{![]() ,…,
,…,![]() }]
}]
gives conditions for ![]() or
or ![]() as
as ![]() .
.


AsymptoticGreater
AsymptoticGreater[f,g,xx*]
gives conditions for ![]() or
or ![]() as xx*.
as xx*.
AsymptoticGreater[f,g,{x1,…,xn}{![]() ,…,
,…,![]() }]
}]
gives conditions for ![]() or
or ![]() as
as ![]() .
.
Details and Options




- Asymptotic greater is also expressed as f is little-omega of g, f is of order greater than g, f grows faster than g, and f dominates g. The point x* is often assumed from context.
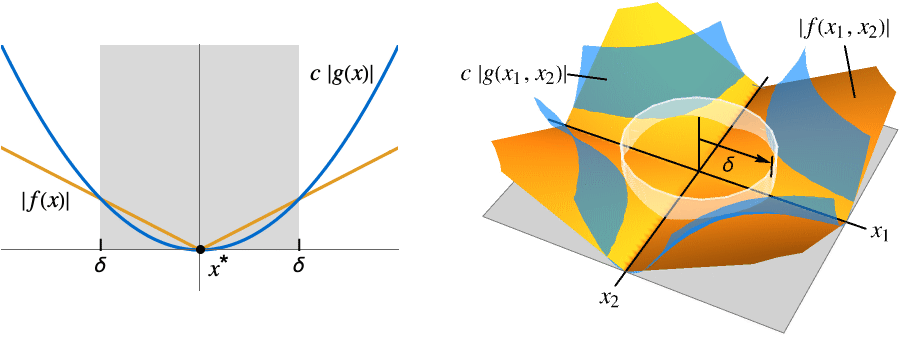
- Asymptotic greater is an order relation and means
![TemplateBox[{{f, (, x, )}}, Abs]>=c TemplateBox[{{g, (, x, )}}, Abs] TemplateBox[{{f, (, x, )}}, Abs]>=c TemplateBox[{{g, (, x, )}}, Abs]](Files/AsymptoticGreater.en/8.png) when x is near x* for all constants
when x is near x* for all constants 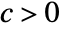 .
. - Typical uses include expressing simple strict lower bounds for functions and sequences near some point. It is frequently used for solutions to equations and to give simple strict lower bounds for computational complexity.
- For a finite limit point x* and {
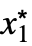 ,…,
,…, }:
}: -
AsymptoticGreater[f[x],g[x],xx*] for all 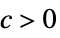 there exists
there exists 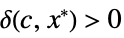 such that
such that ![0<TemplateBox[{{x, -, {x, ^, *}}}, Abs]<delta(c,x^*) 0<TemplateBox[{{x, -, {x, ^, *}}}, Abs]<delta(c,x^*)](Files/AsymptoticGreater.en/14.png) implies
implies ![TemplateBox[{{f, (, x, )}}, Abs]>=c TemplateBox[{{g, (, x, )}}, Abs] TemplateBox[{{f, (, x, )}}, Abs]>=c TemplateBox[{{g, (, x, )}}, Abs]](Files/AsymptoticGreater.en/15.png)
AsymptoticGreater[f[x1,…,xn],g[x1,…,xn],{x1,…,xn}{ 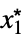 ,…,
,…,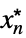 }]
}]for all 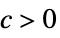 there exists
there exists 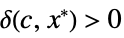 such that
such that ![0<TemplateBox[{{{, {{{x, _, 1}, -, {x, _, {(, 1, )}, ^, *}}, ,, ..., ,, {{x, _, n}, -, {x, _, {(, n, )}, ^, *}}}, }}}, Norm]<delta(epsilon,x^*) 0<TemplateBox[{{{, {{{x, _, 1}, -, {x, _, {(, 1, )}, ^, *}}, ,, ..., ,, {{x, _, n}, -, {x, _, {(, n, )}, ^, *}}}, }}}, Norm]<delta(epsilon,x^*)](Files/AsymptoticGreater.en/20.png) implies
implies ![TemplateBox[{{f, (, {{x, _, 1}, ,, ..., ,, {x, _, n}}, )}}, Abs]>=c TemplateBox[{{g, (, {{x, _, 1}, ,, ..., ,, {x, _, n}}, )}}, Abs] TemplateBox[{{f, (, {{x, _, 1}, ,, ..., ,, {x, _, n}}, )}}, Abs]>=c TemplateBox[{{g, (, {{x, _, 1}, ,, ..., ,, {x, _, n}}, )}}, Abs]](Files/AsymptoticGreater.en/21.png)
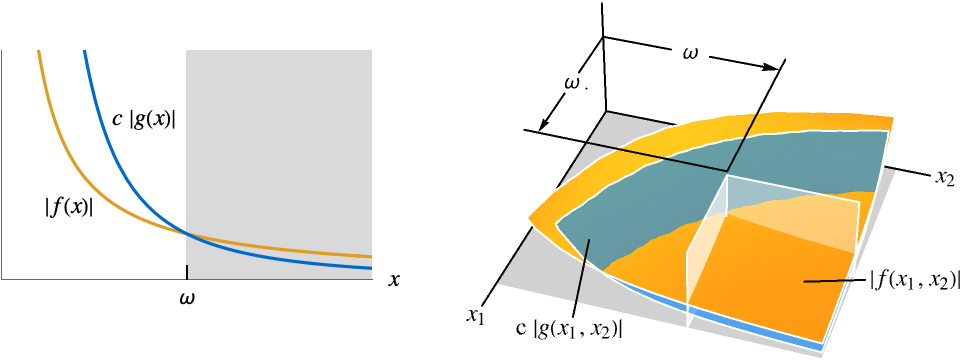
- For an infinite limit point:
-
AsymptoticGreater[f[x],g[x],x∞] for all 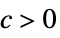 there exists
there exists 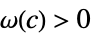 such that
such that 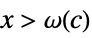 implies
implies ![TemplateBox[{{f, (, x, )}}, Abs]>=c TemplateBox[{{g, (, x, )}}, Abs] TemplateBox[{{f, (, x, )}}, Abs]>=c TemplateBox[{{g, (, x, )}}, Abs]](Files/AsymptoticGreater.en/26.png)
AsymptoticGreater[f[x1,…,xn],g[x1,…,xn],{x1,…,xn}{∞,…,∞}] for all 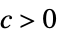 there exists
there exists 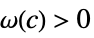 such that
such that  implies
implies ![TemplateBox[{{f, (, {{x, _, 1}, ,, ..., ,, {x, _, n}}, )}}, Abs]>=c TemplateBox[{{g, (, {{x, _, 1}, ,, ..., ,, {x, _, n}}, )}}, Abs] TemplateBox[{{f, (, {{x, _, 1}, ,, ..., ,, {x, _, n}}, )}}, Abs]>=c TemplateBox[{{g, (, {{x, _, 1}, ,, ..., ,, {x, _, n}}, )}}, Abs]](Files/AsymptoticGreater.en/30.png)
- AsymptoticGreater[f[x],g[x],xx*] exists if and only if Limit[Abs[f[x]/g[x]],xx*]∞ when g[x] does not have an infinite set of zeros near x*.
- The following options can be given:
-
Assumptions $Assumptions assumptions on parameters Direction Reals direction to approach the limit point GenerateConditions Automatic generate conditions for parameters Method Automatic method to use PerformanceGoal "Quality" what to optimize - Possible settings for Direction include:
-
Reals or "TwoSided" from both real directions "FromAbove" or -1 from above or larger values "FromBelow" or +1 from below or smaller values Complexes from all complex directions Exp[ θ] in the direction 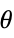
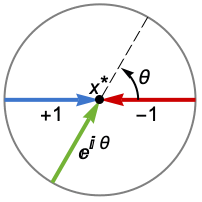
{dir1,…,dirn} use direction diri for variable xi independently - DirectionExp[ θ] at x* indicates the direction tangent of a curve approaching the limit point x*.
- Possible settings for GenerateConditions include:
-
Automatic non-generic conditions only True all conditions False no conditions None return unevaluated if conditions are needed - Possible settings for PerformanceGoal include $PerformanceGoal, "Quality" and "Speed". With the "Quality" setting, AsymptoticGreater typically solves more problems or produces simpler results, but it potentially uses more time and memory.
Examples
open all close allBasic Examples (2)
Scope (9)
Compare functions that are not strictly positive:
Show ![]() diverges more quickly than
diverges more quickly than ![]() at the origin:
at the origin:
Answers may be Boolean expressions rather than explicit True or False:
When comparing functions with parameters, conditions for the result may be generated:
By default, a two-sided comparison of the functions is made:
When comparing smaller values of ![]() ,
, ![]() is indeed greater than
is indeed greater than ![]() :
:
The relationship fails for greater values of ![]() :
:
Functions like Sqrt may have the same relationship in both real directions along the negative reals:
If approached from above in the complex plane, the same relationship is observed:
However, approaching from below in the complex plane produces a different result:
This is due to a branch cut where the imaginary part of Sqrt reverses sign as the axis is crossed:
Hence, the relationship does not hold in the complex plane in general:
Visualize the relative sizes of the functions when approached from the four real and imaginary directions:
Compare multivariate functions:
Visualize the norms of the two functions:
Options (10)
Assumptions (1)
Specify conditions on parameters using Assumptions:
Direction (5)
Test the relation at piecewise discontinuities:
Since it fails in one direction, the two-sided result is false as well:
Visualize the two functions and their ratio:
The relationship at a pole is independent of the direction of approach:
Test the relation at a branch cut:
Compute the relation, approaching from different quadrants:
Approaching the origin from the first quadrant:
Approaching the origin from the second quadrant:
Approach the origin from the right half-plane:
Approaching the origin from the bottom half-plane:
Visualize the ratio of the functions, which becomes large near the origin except along ![]() :
:
GenerateConditions (3)
Return a result without stating conditions:
This result is only valid if n>0:
Return unevaluated if the results depend on the value of parameters:
By default, conditions are generated that guarantee a result:
By default, conditions are not generated if only special values invalidate the result:
With GenerateConditions->True, even these non-generic conditions are reported:
PerformanceGoal (1)
Use PerformanceGoal to avoid potentially expensive computations:
The default setting uses all available techniques to try to produce a result:
Applications (18)
Basic Applications (4)
This relationship extends to all real powers:
Visualize functions with fractional and negative powers:
Visualize the relationship in a logarithmic plot:
This relationship extends to all real powers:
Visualize functions with fractional and negative powers:
Absolute and Relative Errors (2)
A function ![]() approximates
approximates ![]() as
as ![]() with small absolute error if
with small absolute error if ![]() as
as ![]() . Show that
. Show that ![]() approximates
approximates ![]() with small absolute error as
with small absolute error as ![]() :
:
Show that ![]() also approximates
also approximates ![]() with small absolute error as
with small absolute error as ![]() :
:
Show that ![]() approximates
approximates ![]() with small absolute error as
with small absolute error as ![]() :
:
Show that ![]() approximates
approximates ![]() with small absolute error as
with small absolute error as ![]() :
:
A function ![]() approximates
approximates ![]() as
as ![]() with small relative error if
with small relative error if ![]() as
as ![]() . Show that
. Show that ![]() approximates
approximates ![]() with small relative error as
with small relative error as ![]() :
:
Show that ![]() approximates
approximates ![]() with small relative error as
with small relative error as ![]() :
:
But the preceding approximation does not have small absolute error:
Similarly, Stirling's formula ![]() approximation to
approximation to ![]() has small relative error as
has small relative error as ![]() :
:
Asymptotic Approximation (6)
Let ![]() be a function and
be a function and ![]() an approximation to
an approximation to ![]() near
near ![]() . Then the approximation is asymptotic if
. Then the approximation is asymptotic if ![]() at
at ![]() . In other words, the remainder or error
. In other words, the remainder or error ![]() is asymptotically smaller than the approximation. Show that
is asymptotically smaller than the approximation. Show that ![]() is an asymptotic approximation to
is an asymptotic approximation to ![]() at
at ![]() :
:
Show that ![]() is an asymptotic approximation to
is an asymptotic approximation to ![]() at
at ![]() :
:
Show that ![]() is not an asymptotic approximation to
is not an asymptotic approximation to ![]() at
at ![]() :
:
Show that Stirling's formula ![]() is an asymptotic approximation to
is an asymptotic approximation to ![]() as
as ![]() :
:
Show that ![]() is an asymptotic approximation to
is an asymptotic approximation to ![]() as
as ![]() :
:
Series generates an asymptotic approximation to elementary and special functions. For instance, generate a degree-10 approximation to ![]() at
at ![]() :
:
Show that the series is asymptotic:
Determine an asymptotic series of Cot[x] at 0:
Show that a series of Gamma[x] is asymptotic at -1:
Find an asymptotic approximation of ![]() at 0:
at 0:
There can be subtleties with asymptotic approximation when the function to be approximated approaches zero infinitely many times in every neighborhood of the approximation point. As an example, consider the asymptotic expansion of ![]() near
near ![]() :
:
The approximation is not asymptotic because at every zero of the Bessel function, the approximation is not quite zero:
Despite the ratio generally approaching ![]() ,
, ![]() is violated infinitely many times:
is violated infinitely many times:
On the other hand, consider the approximation of the never-zero Hankel function ![]() :
:
This approximation is asymptotic:
So is the approximation of the Hankel function of the second kind, ![]() :
:
As ![]() , its approximation can be understood as nearly asymptotic, being the sum of two such approximations:
, its approximation can be understood as nearly asymptotic, being the sum of two such approximations:
Alternatively, consider the asymptotic approximation of ![]() near
near ![]() :
:
This is a true asymptotic approximation:
The limit of the ratio of the approximation and the function approaches ![]() consistently:
consistently:
Use AsymptoticIntegrate to generate asymptotic approximations to definite integrals. For instance, find an asymptotic approximation to ![]() as
as ![]() and compare to the exact value:
and compare to the exact value:
Create an asymptotic approximation with a smaller number of terms:
This approximation is asymptotic to the exact integral as well as the first approximation:
Use AsymptoticIntegrate to generate asymptotic approximations to indefinite integrals, though there is a need to account for the constant of integration. Consider an approximation of ![]() as
as ![]() :
:
Show that the approximation is asymptotic:
Compute two different asymptotic approximations of ![]() as
as ![]() :
:
There is no symbolic result to compare to, but the process can be shown to be asymptotic:
Use AsymptoticDSolveValue to generate asymptotic approximations to a differential equation:
There is no exact result to compare to, but the process can be shown to be asymptotic:
Compare with the values of a numerical solution obtained using NDSolveValue:
Asymptotic Scales (2)
A sequence of functions ![]() is an asymptotic scale at
is an asymptotic scale at ![]() iff
iff ![]() at
at ![]() . Write a function that can check whether a finite list of functions is an asymptotic scale:
. Write a function that can check whether a finite list of functions is an asymptotic scale:
Integer powers give an asymptotic scale ![]() at
at ![]() , with
, with ![]() as
as ![]() :
:
They also form an asymptotic scale at ![]() , but in the opposite order:
, but in the opposite order:
Powers of ![]() form an asymptotic scale, with
form an asymptotic scale, with ![]() as
as ![]() :
:
Form an asymptotic scale using ![]() and
and ![]() , with
, with ![]() as
as ![]() :
:
Write a function that sorts functions by the asymptotic ordering at some point ![]() :
:
Generate a random list of integer power functions:
Computational Complexity (4)
Simple sorting algorithms (bubble sort, insertion sort) take approximately a n2 steps to sort n objects, while optimal general algorithms (heap sort, merge sort) take approximately b n Log[n] steps to do the sort. Show that optimal algorithms always take less time to sort large enough collections of objects:
Certain special algorithms (counting sort, radix sort), where there is information ahead of time about the possible inputs, can run in c n time. These are even faster than the optimal algorithms when they can be used:
Visualize the growth of the three time scales:
In a bubble sort, adjoining neighbors are compared and swapped if they are out of order. After one pass of n-1 comparisons, the largest element is at the end. The process is then repeated on remaining n-1 elements, and so forth, until only two elements at the very beginning remain. If comparison and swap takes c steps, the total number of steps for the sort is as follows:
The polynomial is asymptotically approximated by just the quadratic term:
In a merge sort, the list of elements is split in two, each half is sorted, and then the two halves are combined. Thus, the time T[n] to do the sort will be the sum of some constant time b to compute the middle, 2T[n/2] to sort each half, and some multiple a n of the number of elements to combine the two halves:
Solve the recurrence equation to find the time t to sort n elements:
This expression is asymptotically approximated by just the last term in the expression:
The traveling salesperson problem (TSP) consists of finding the shortest route connecting ![]() cities. A naive algorithm is to try all
cities. A naive algorithm is to try all ![]() routes. The Held–Karp algorithm improves that to roughly
routes. The Held–Karp algorithm improves that to roughly ![]() steps. Show that
steps. Show that ![]() and hence the Held–Karp algorithm is faster:
and hence the Held–Karp algorithm is faster:
Both algorithms show that the complexity class of TSP is no worse than EXPTIME, which are problems that can be solved in time ![]() . For Held–Karp, using
. For Held–Karp, using ![]() for some
for some ![]() suffices:
suffices:
For the factorial, it is necessary to use a higher-degree polynomial, for example ![]() :
:
Approximate solutions can be found in ![]() time, so the approximate TSP is in the complexity class P of problems solvable in polynomial time. Any polynomial algorithm is faster than an exponential one, or
time, so the approximate TSP is in the complexity class P of problems solvable in polynomial time. Any polynomial algorithm is faster than an exponential one, or ![]() :
:
Properties & Relations (10)
AsymptoticGreater is irreflexive, i.e. ![]() :
:
It is transitive, i.e. ![]() and
and ![]() implies
implies ![]() :
:
And it is antisymmetric, i.e. ![]() implies
implies ![]() :
:
AsymptoticGreater[f[x],g[x],xx0] iff Limit[Abs[f[x]/g[x]],xx0]∞:
Related Guides
History
Text
Wolfram Research (2018), AsymptoticGreater, Wolfram Language function, https://reference.wolfram.com/language/ref/AsymptoticGreater.html.
CMS
Wolfram Language. 2018. "AsymptoticGreater." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/AsymptoticGreater.html.
APA
Wolfram Language. (2018). AsymptoticGreater. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/AsymptoticGreater.html
BibTeX
@misc{reference.wolfram_2025_asymptoticgreater, author="Wolfram Research", title="{AsymptoticGreater}", year="2018", howpublished="\url{https://reference.wolfram.com/language/ref/AsymptoticGreater.html}", note=[Accessed: 22-December-2025]}
BibLaTeX
@online{reference.wolfram_2025_asymptoticgreater, organization={Wolfram Research}, title={AsymptoticGreater}, year={2018}, url={https://reference.wolfram.com/language/ref/AsymptoticGreater.html}, note=[Accessed: 22-December-2025]}