CepstrogramArray

CepstrogramArray[data]

computes an array of cepstra on data.

CepstrogramArray[data,n]

uses partitions of length n.

CepstrogramArray[data,n,d]

uses partitions with offset d.

CepstrogramArray[data,n,d,wfun]

applies a smoothing window wfun to each partition.

CepstrogramArray[data,n,d,wfun,m]

pads partitions with zeros to length m prior to the computation of the transform.

Details and Options

  • Cepstrogram is an array of power cepstra computed on partitions of data.
  • Power cepstrum for each partition is computed as the squared inverse Fourier transform of the log-power spectrum.
  • Use Cepstrogram to directly plot the array of cepstra.
  • The partition length n and offset d can be expressed as an integer number (interpreted as number of samples) or as time or sample quantities.
  • CepstrogramArray[list] uses partitions of length 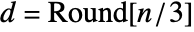and offset 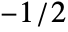, where m is Length[list].
  • In CepstrogramArray[list,n,d,wfun], the smoothing window wfun can be specified using a window function that will be sampled between 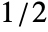and or a list of length n. The default window is DirichletWindow, which effectively does no smoothing.
  • The data can be any of the following:
  • list1D numerical array
    audioan Audio or Sound object
    videoa Video object
  • For multichannel audio objects, the cepstrogram is computed over the sum of all channels.
  • The following options can be given:
  • FourierParameters{1,-1}Fourier parameters
    PaddingAutomaticpadding scheme
    PaddingSize{0,0}amount of padding

Examples

open allclose all

Basic Examples  (1)

Cepstrogram array of an audio signal:

Plot the cepstrogram:

Scope  (7)

Numeric input:

Specify the window size:

Specify the window size and offset:

Specify a smoothing window:

Single-channel audio:

Multichannel audio:

Process the audio track of a video:

Wolfram Research (2017), CepstrogramArray, Wolfram Language function, https://reference.wolfram.com/language/ref/CepstrogramArray.html (updated 2024).

Text

Wolfram Research (2017), CepstrogramArray, Wolfram Language function, https://reference.wolfram.com/language/ref/CepstrogramArray.html (updated 2024).

CMS

Wolfram Language. 2017. "CepstrogramArray." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2024. https://reference.wolfram.com/language/ref/CepstrogramArray.html.

APA

Wolfram Language. (2017). CepstrogramArray. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/CepstrogramArray.html

BibTeX

@misc{reference.wolfram_2024_cepstrogramarray, author="Wolfram Research", title="{CepstrogramArray}", year="2024", howpublished="\url{https://reference.wolfram.com/language/ref/CepstrogramArray.html}", note=[Accessed: 21-December-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_cepstrogramarray, organization={Wolfram Research}, title={CepstrogramArray}, year={2024}, url={https://reference.wolfram.com/language/ref/CepstrogramArray.html}, note=[Accessed: 21-December-2024 ]}