Cosh
Cosh[z]
gives the hyperbolic cosine of z.
Details
- Mathematical function, suitable for both symbolic and numerical manipulation.
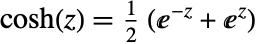 .
.- For certain special arguments, Cosh automatically evaluates to exact values.
- Cosh can be evaluated to arbitrary numerical precision.
- Cosh automatically threads over lists. »
- Cosh can be used with Interval and CenteredInterval objects. »
Background & Context
- Cosh is the hyperbolic cosine function, which is the hyperbolic analogue of the Cos circular function used throughout trigonometry. It is defined for real numbers by letting
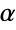 be twice the area between the
be twice the area between the 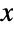 axis and a ray through the origin intersecting the unit hyperbola
axis and a ray through the origin intersecting the unit hyperbola 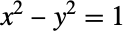 . Cosh[α] then represents the horizontal coordinate of the intersection point. Cosh may also be defined as
. Cosh[α] then represents the horizontal coordinate of the intersection point. Cosh may also be defined as 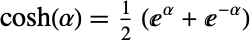 , where
, where 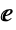 is the base of the natural logarithm Log.
is the base of the natural logarithm Log. - Cosh automatically evaluates to exact values when its argument is the (natural) logarithm of a rational number. When given exact numerical expressions as arguments, Cosh may be evaluated to arbitrary numeric precision. Other operations useful for manipulation of symbolic expressions involving Cosh include TrigToExp, TrigExpand, Simplify, and FullSimplify.
- Cosh threads element-wise over lists and matrices. In contrast, MatrixFunction can be used to give the hyperbolic cosine of a square matrix (i.e. the power series for the hyperbolic cosine function with ordinary powers replaced by matrix powers) as opposed to the hyperbolic cosines of the individual matrix elements.
- Cosh[x] increases exponentially as x approaches
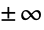 . Cosh satisfies an identity similar to the Pythagorean identity satisfied by Cos, namely
. Cosh satisfies an identity similar to the Pythagorean identity satisfied by Cos, namely 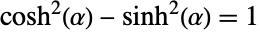 . The definition of the hyperbolic sine function is extended to complex arguments
. The definition of the hyperbolic sine function is extended to complex arguments 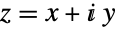 by way of the identity
by way of the identity 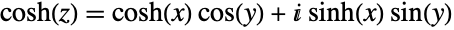 . The hyperbolic cosine function is entire, meaning it is complex differentiable at all finite points of the complex plane. Cosh[z] has series expansion
. The hyperbolic cosine function is entire, meaning it is complex differentiable at all finite points of the complex plane. Cosh[z] has series expansion 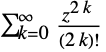 about the origin.
about the origin. - The inverse function of Cosh is ArcCosh. Additional related mathematical functions include Sinh and Sech.
Examples
open allclose allBasic Examples (4)
Scope (48)
Numerical Evaluation (6)
The precision of the output tracks the precision of the input:
Cosh can take complex number inputs:
Evaluate Cosh efficiently at high precision:
Compute the elementwise values of an array using automatic threading:
Or compute the matrix Cosh function using MatrixFunction:
Compute worst-case guaranteed intervals using Interval and CenteredInterval objects:
Or compute average-case statistical intervals using Around:
Specific Values (4)
Values of Cosh at fixed, purely imaginary points:
Minimum of Cosh:
Find the minimum as the root of ![]() :
:
Simple exact values are generated automatically:
More complicated cases require explicit use of FunctionExpand:
Visualization (3)
Function Properties (12)
Cosh is defined for all real and complex values:
Cosh achieves all real values greater than or equal to 1:
The range for complex values is the whole plane:
Cosh is an even function:
Cosh has the mirror property ![]() :
:
Cosh is an analytic function of x:
Cosh is neither non-decreasing nor non-increasing:
Cosh is not injective:
Cosh is not surjective:
Cosh is non-negative:
Has no singularities or discontinuities:
Cosh is convex:
TraditionalForm formatting:
Integration (4)
Series Expansions (4)
Integral Transforms (2)
Function Identities and Simplifications (6)
Function Representations (4)
Representation through Cos:
Representation through Bessel functions:
Representation in terms of MeijerG:
Cosh can be represented as a DifferentialRoot:
Applications (10)
Build rotation matrix in hyperbolic space from infinitesimal transformations:
The matrix is orthogonal with respect to the Minkowski metric:
Construct a relativistic coordinate transformation for rapidity η:
Special solution of the sine–Gordon equation:
Pythagorean theorem in hyperbolic geometry:
The small t limit gives the ordinary Pythagorean theorem:
Solve a differential equation:
Find the hyperbolic forms of solutions to differential equations:
Show that ![]() approximates
approximates ![]() with small absolute error as
with small absolute error as ![]() :
:
Find a point in the hyperbola using Cosh and Sinh functions:
Properties & Relations (12)
Basic parity and periodicity properties of Cosh get automatically applied:
Expressions containing hyperbolic functions do not automatically simplify:
Use Simplify:
Compose with inverse functions:
Numerically find a root of a transcendental equation:
Cosh appears in special cases of many mathematical functions:
Cosh is a numeric function:
The generating function for Cosh:
The exponential generating function for Cosh:
Possible Issues (5)
Machine-precision input is insufficient to give a correct answer:
With exact input, the answer is correct:
A larger setting for $MaxExtraPrecision can be needed:
Machine-number inputs can give high‐precision results:
No power series exists at infinity, where Cosh has an essential singularity:
In TraditionalForm, parentheses are needed around the argument:
Text
Wolfram Research (1988), Cosh, Wolfram Language function, https://reference.wolfram.com/language/ref/Cosh.html (updated 2021).
CMS
Wolfram Language. 1988. "Cosh." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2021. https://reference.wolfram.com/language/ref/Cosh.html.
APA
Wolfram Language. (1988). Cosh. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Cosh.html