FindPeaks

FindPeaks[list]

gives positions and values of the detected peaks in list.

FindPeaks[list,σ]

finds peaks that survive Gaussian blurring up to scale σ.

FindPeaks[list,σ,s]

finds peaks with minimum sharpness s.

FindPeaks[list,σ,s,t]

finds only peaks with values greater than t.

FindPeaks[list,σ,{s,σs},{t,σt}]

uses different scales for thresholding sharpness and value.

Details and Options

  • FindPeaks finds local maxima using the given constraints, returning the result as {{x1,y1},{x2,y2},…}.
  • Input list can be of one of the following forms:
  • {y1,y2,…}a list of values
    TimeSeries[…]regularly sampled time series object
    EventSeries[…]regularly sampled event series object
  • FindPeaks[list] automatically chooses scale, sharpness and threshold parameters.
  • To avoid the detection of noise-related peaks, the input is regularized by performing a Gaussian filtering using the standard deviation σ.
  • The value of σ defaults to 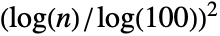, with n being the number of data points in list. Larger values for σ reduce the number of peaks.
  • Peaks detected in the regularized data are traced back to the corresponding peaks in the original data.
  • By default, peaks are not filtered based on their sharpness (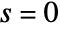). The sharpness s is computed as the second derivative of the data with a Gaussian filter at scale σ. Specify a smaller scale using {s,σs}.
  • By default, peaks of any height are returned. Use a threshold t to dismiss peaks with smaller values. To apply the threshold at a scale other than 0, use {t,σt}.
  • FindPeaks[list,σ,s,t] is equivalent to FindPeaks[list,σ,{s,σ},{t,0}].
  • The following options can be given:
  • InterpolationOrderAutomaticspline interpolation order of up to order 3
    Padding"Reflected"padding scheme to use
  • By default, InterpolationOrder1 is assumed for lists of data. For TimeSeries objects, the interpolation order is inherited.
  • The interpolation order is used when computing peak positions. Peaks may be located in between and possibly above {x,y} samples interpolation orders.
  • For interpolation orders 0 or 1, a plateau of two or more data samples is assigned a single peak at its center location.
  • For possible settings for Padding, see the reference page for ArrayPad.

Examples

open allclose all

Basic Examples  (1)

Find position and height of dominant peaks in a list:

Visualize list and the detected peaks:

Scope  (12)

Data  (4)

Peaks of a 1D list:

Peaks of a TimeSeries object:

Peaks of an EventSeries object:

Find peaks:

Peaks of a list of Quantity objects:

Threshold for values greater than 30 meters:

Parameters  (8)

By default, an automatic scale is used:

Find all peaks at scale :

Compute peaks at different scales:

When finding peaks at scale , only peaks that sustain a blur up to scale are returned:

Signal and its blurred version at scale :

By default, peaks are not filtered based on their sharpness, equivalent to :

Specify minimum sharpness value :

Sharpness, defined by the negative second derivative, should be greater than the specified s:

Specify a minimum height value :

Apply the value threshold after smoothing the data using a scale :

Options  (3)

InterpolationOrder  (1)

By default, InterpolationOrder1 is used:

Find peaks of the cubic interpolation:

Note that the number and position of peaks may vary depending on the interpolation order:

Padding  (2)

By default, Padding"Reflected" is used:

Specify a constant padding:

Padding influences the occurrence and position of peaks at the boundary:

By default, "Reflected" padding causes a peak at position 1:

"Reversed" padding induces a peak at position 1/2:

"Fixed" padding results in no peak at the boundary:

Applications  (6)

Find peaks in the stock price of Apple in the year 2013:

Highlight peaks on the plot of the data:

Find peaks in elevation data:

Mean daily temperatures for Chicago during a period of two months:

Find peaks in the temperature:

Find peaks in an ECG signal:

Detect the mode of a distribution using the peak of its histogram. Sample a Fréchet distribution:

Find the mode of the distribution:

Compare the mode with the theoretical value of the Fréchet distribution:

Use peaks of an audio power spectrum to detect pitches of the sound:

Compute the power periodogram:

Find peaks of the power spectrum:

Converting peak locations into corresponding frequencies:

Wolfram Research (2014), FindPeaks, Wolfram Language function, https://reference.wolfram.com/language/ref/FindPeaks.html (updated 2021).

Text

Wolfram Research (2014), FindPeaks, Wolfram Language function, https://reference.wolfram.com/language/ref/FindPeaks.html (updated 2021).

CMS

Wolfram Language. 2014. "FindPeaks." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2021. https://reference.wolfram.com/language/ref/FindPeaks.html.

APA

Wolfram Language. (2014). FindPeaks. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/FindPeaks.html

BibTeX

@misc{reference.wolfram_2022_findpeaks, author="Wolfram Research", title="{FindPeaks}", year="2021", howpublished="\url{https://reference.wolfram.com/language/ref/FindPeaks.html}", note=[Accessed: 05-October-2022 ]}

BibLaTeX

@online{reference.wolfram_2022_findpeaks, organization={Wolfram Research}, title={FindPeaks}, year={2021}, url={https://reference.wolfram.com/language/ref/FindPeaks.html}, note=[Accessed: 05-October-2022 ]}