MomentOfInertia[reg,pt,v]
computes the moment of inertia for the region reg rotating around an axis through the point pt in direction v.
MomentOfInertia[reg]
computes the moment of inertia matrix for the region reg relative to the center of mass.
MomentOfInertia[reg,pt]
computes the moment of inertia matrix relative to the point pt.


MomentOfInertia
MomentOfInertia[reg,pt,v]
computes the moment of inertia for the region reg rotating around an axis through the point pt in direction v.
MomentOfInertia[reg]
computes the moment of inertia matrix for the region reg relative to the center of mass.
MomentOfInertia[reg,pt]
computes the moment of inertia matrix relative to the point pt.
Details and Options

- Moment of inertia is also known as rotational inertia, area moment of inertia, and mass moment of inertia. The moment of inertia matrix is also known as rotational inertia matrix and angular mass matrix.
- Moment of inertia is the resistance to rotational acceleration for rigid bodies and is the rotational analog of mass, which is the resistance to translational acceleration.
-
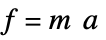
translational acceleration force 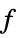 , acceleration
, acceleration 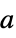 , mass
, mass 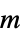
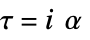
rotational acceleration torque  , rotational acceleration
, rotational acceleration  , moment of inertia
, moment of inertia 
- MomentOfInertia[reg,pt] gives the moment of inertia matrix about the point pt and is given by
-
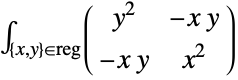
2D moment of inertia matrix 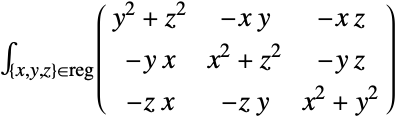
3D moment of inertia matrix - where reg is the region reg translated by -pt.
- The moment of inertia matrix ℐ can be used to compute the moment of inertia for any direction v through the formula
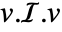 , where in 2D it is required that v be in the
, where in 2D it is required that v be in the 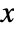 -
-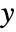 plane. »
plane. » - MomentOfInertia computes a result under the assumption that the mass density of the region is constant.
- For varying mass density
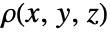 , use Integrate or NIntegrate to compute the corresponding moment of inertia matrix according to the following formula. »
, use Integrate or NIntegrate to compute the corresponding moment of inertia matrix according to the following formula. » -
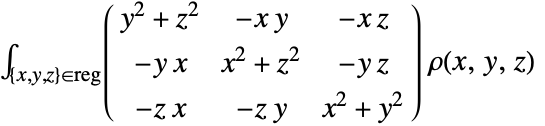
Examples
open all close allBasic Examples (4)
The moment of inertia when rotating around the axis through ![]() and in direction
and in direction ![]() :
:
If the vector is omitted, you get a moment of inertia matrix about that point:
Using this matrix and a normalized vector, the moment of inertia around any axis can be found:
If the point is omitted, you get a moment of inertia matrix around the center of mass:
This is equivalent to specifying the center point by RegionCentroid:
Compute the moment of inertia for a region with symbolic parameters:
Scope (24)
Special Regions (15)
Rectangle with length ![]() and width
and width ![]() :
:
Disk with radius ![]() :
:
Annulus with radii ![]() and
and ![]() :
:
StadiumShape with length ![]() and radius
and radius ![]() :
:
Right Triangle with sides ![]() and
and ![]() :
:
Cuboid with length ![]() , width
, width ![]() , and height
, and height ![]() :
:
Ball with radius ![]() :
:
Ellipsoid with semiaxes ![]() ,
, ![]() , and
, and ![]() :
:
SphericalShell with radii ![]() and
and ![]() :
:
Cylinder with length ![]() and radius
and radius ![]() :
:
CapsuleShape with length ![]() and radius
and radius ![]() :
:
Rectangular Tetrahedron with sides ![]() ,
, ![]() , and
, and ![]() :
:
Rectangular Pyramid with sides ![]() ,
, ![]() and height
and height ![]() :
:
Rectangular Prism with sides ![]() ,
, ![]() and height
and height ![]() :
:
Formula Regions (2)
The inertia matrix of a disk represented as an ImplicitRegion:
Moment of inertia for a cylinder:
The moment of inertia of a disk represented as a ParametricRegion:
Mesh Regions (2)
The moment of inertia matrix of a MeshRegion in 2D:
The moment of inertia matrix of a BoundaryMeshRegion:
Derived Regions (3)
The moment of inertia of a RegionIntersection:
The moment of inertia matrix of a TransformedRegion:
The moment of inertia matrix of a RegionBoundary:
Geographic Regions (2)
MomentOfInertia works on polygons of geographic entities:
Polygons with GeoPosition:
Polygons with GeoPositionXYZ:
Polygons with GeoPositionENU:
The moment of inertia of a polygon with GeoGridPosition:
Applications (11)
MomentOfInertia gives the moment of inertia for a body with constant mass density 1. Compute the moment of inertia for a Cuboid with length ![]() , width
, width ![]() , height
, height ![]() , and a constant mass density
, and a constant mass density ![]() :
:
The mass of a body with a constant mass density ![]() is given by m=ρ Volume[body]. Express the moment of inertia in terms of mass
is given by m=ρ Volume[body]. Express the moment of inertia in terms of mass ![]() of the body:
of the body:
Moment of inertia of a 2D region embedded in 3D:
The top-left 2×2 submatrix is equal to moment of inertia of the 2D region:
The only other nonzero entry of the matrix is on the diagonal. It is the polar moment of area about the ![]() axis and, by the perpendicular axis theorem, it is equal to the sum of the other two entries on the diagonal:
axis and, by the perpendicular axis theorem, it is equal to the sum of the other two entries on the diagonal:
The principal axes for a body are given by the eigenvectors of the moment of inertia matrix:
When a moment of inertia matrix is diagonal, then the principal axes coincide with the coordinate axes:
In this case, the principal axes coincide with the coordinate axes:
A moment of inertia matrix can be thought as a matrix defining an Ellipsoid:
The inertia ellipsoid is defined as ![]() , where
, where ![]() is the centroid:
is the centroid:
Use Eigensystem to find the principal axes:
Show inertial ellipsoid together with its principal axes:
The angular momentum for a rotating rigid body is given by ![]() , where
, where ![]() is the moment of inertia and
is the moment of inertia and ![]() is the angular velocity. Suppose a ball of radius 1 and uniform density 1 rotates around the
is the angular velocity. Suppose a ball of radius 1 and uniform density 1 rotates around the ![]() axis on a string with adjustable length
axis on a string with adjustable length ![]() . When
. When ![]() , the angular velocity is
, the angular velocity is ![]() . Find the angular velocity
. Find the angular velocity ![]() as a function of
as a function of ![]() :
:
Compute ![]() knowing that, according to the angular momentum conservation law, if no torque is applied to a body, its angular momentum
knowing that, according to the angular momentum conservation law, if no torque is applied to a body, its angular momentum ![]() remains constant:
remains constant:
The kinetic energy for a rotating rigid body is given by ![]() , where
, where ![]() is the moment of inertia and
is the moment of inertia and ![]() is the angular velocity. Compute the kinetic energy of a ball with radius
is the angular velocity. Compute the kinetic energy of a ball with radius ![]() and uniform density
and uniform density ![]() , rotating with angular velocity
, rotating with angular velocity ![]() around an axis passing through its center:
around an axis passing through its center:
A kinetic energy recovery system (KERS) stores kinetic energy for a car when braking. Suppose the energy is stored in a rotating steel cylinder with radius ![]() and length
and length ![]() . How fast does the cylinder need to rotate to store
. How fast does the cylinder need to rotate to store ![]() of energy, assuming the density of steel is
of energy, assuming the density of steel is ![]() :
:
The moment of inertia for the steel cylinder:
Find the required angular velocity for ![]() storage:
storage:
In terms of revolutions per minute:
The kinetic energy for a rigid body is given by ![]() , where
, where ![]() is an angular velocity vector and
is an angular velocity vector and ![]() is the moment of inertia matrix. Find the rotational energy for a cuboid with sides 2, 4, and 6 when rotating around different axes. In all cases, the mass of the rotating body is the same, but how the mass is distributed relative to the rotation axis differs and is represented by moment of inertia:
is the moment of inertia matrix. Find the rotational energy for a cuboid with sides 2, 4, and 6 when rotating around different axes. In all cases, the mass of the rotating body is the same, but how the mass is distributed relative to the rotation axis differs and is represented by moment of inertia:
For a rotating rigid body, the relation between the torque ![]() and the angular acceleration
and the angular acceleration ![]() is given by
is given by ![]() , where
, where ![]() is the moment of inertia. Compute the torque required to give a cube with one-meter sides of lead and angular acceleration of
is the moment of inertia. Compute the torque required to give a cube with one-meter sides of lead and angular acceleration of ![]() :
:
Compute the moment of inertia, assuming the density of lead is ![]() :
:
The parallel axis theorem gives a relation ![]() between the moment of inertia
between the moment of inertia ![]() around an arbitrary axis and the moment of inertia
around an arbitrary axis and the moment of inertia ![]() around the parallel axis passing through the center of mass, where
around the parallel axis passing through the center of mass, where ![]() is the total mass and
is the total mass and ![]() is the distance between the axes:
is the distance between the axes:
Properties & Relations (11)
If the point is omitted, the RegionCentroid is taken as a default:
For a given point ![]() , one will get the same result by translating the body by
, one will get the same result by translating the body by ![]() and calculating the moment of inertia around the origin:
and calculating the moment of inertia around the origin:
The moment of inertia is the integral of square distance to the axis of rotation:
The moment of inertia matrix is defined by an integral over the body:
Use Integrate to compute moment of inertia for a body varying mass density ![]() :
:
The moment of inertia matrix is symmetric:
The moment of inertia matrix is positive semidefinite:
Moment of inertia matrix in 2D can be computed using RegionMoment:
Moment of inertia matrix in 3D can be computed using RegionMoment:
The moment of inertia of a Point is the square of the distance of the point to the axis:
For a set of points, it is the sum of moments of inertia:
The moment of inertia for disjoint bodies is the sum of moments of inertia:
Related Guides
History
Text
Wolfram Research (2016), MomentOfInertia, Wolfram Language function, https://reference.wolfram.com/language/ref/MomentOfInertia.html.
CMS
Wolfram Language. 2016. "MomentOfInertia." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/MomentOfInertia.html.
APA
Wolfram Language. (2016). MomentOfInertia. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/MomentOfInertia.html
BibTeX
@misc{reference.wolfram_2025_momentofinertia, author="Wolfram Research", title="{MomentOfInertia}", year="2016", howpublished="\url{https://reference.wolfram.com/language/ref/MomentOfInertia.html}", note=[Accessed: 07-October-2025]}
BibLaTeX
@online{reference.wolfram_2025_momentofinertia, organization={Wolfram Research}, title={MomentOfInertia}, year={2016}, url={https://reference.wolfram.com/language/ref/MomentOfInertia.html}, note=[Accessed: 07-October-2025]}