ContinuousMarkovProcess[i0,q]
represents a continuous-time finite-state Markov process with transition rate matrix q and initial state i0.
ContinuousMarkovProcess[p0,q]
represents a Markov process with initial state probability vector p0.
ContinuousMarkovProcess[…,m,μ]
represents a Markov process with transition matrix m and transition rates μ.
represents a Markov process transition rate matrix from the graph g.


ContinuousMarkovProcess
ContinuousMarkovProcess[i0,q]
represents a continuous-time finite-state Markov process with transition rate matrix q and initial state i0.
ContinuousMarkovProcess[p0,q]
represents a Markov process with initial state probability vector p0.
ContinuousMarkovProcess[…,m,μ]
represents a Markov process with transition matrix m and transition rates μ.
represents a Markov process transition rate matrix from the graph g.
Details

- ContinuousMarkovProcess is also known as a continuous-time Markov chain.
- ContinuousMarkovProcess is a continuous-time and discrete-state random process.
- The states of ContinuousMarkovProcess are integers between 1 and
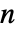 , where
, where 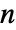 is the length of transition rate matrix q.
is the length of transition rate matrix q. - For infinitesimal time dt, q〚i,j〛dt gives the probability that the process transitions from state i to state j over the next dt units of time q〚i,j〛dtProbability[x[t+dt]jx[t]i].
- The time the process stays in state i before transitioning follows ExponentialDistribution[-qii].
- The transition matrix m specifies conditional transition probabilities m〚i,j〛Probability[x[tk+1]jx[tk]i], where x[tk] is the state at time tk, and the transition rate μi specifies that the time between events in state
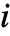 follows ExponentialDistribution[μi].
follows ExponentialDistribution[μi]. - EstimatedProcess[data,ContinuousMarkovProcess[n]] indicates that process with n states should be estimated.
- The transition matrix in the case of a graph g is constructed to give equal probability of transitioning to each incident vertex with unit transition rates.
- ContinuousMarkovProcess allows q to be an
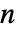 ×
×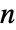 matrix where
matrix where 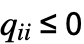 and
and 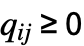 for
for 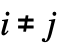 with rows that sum to 0, i0 can be an integer between 1 and
with rows that sum to 0, i0 can be an integer between 1 and 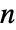 , p0 is a vector of length
, p0 is a vector of length 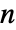 of non-negative elements that sum to 1, m is an
of non-negative elements that sum to 1, m is an 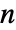 ×
×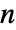 matrix with non-negative elements and rows that sum to 1, and μ is a vector of length
matrix with non-negative elements and rows that sum to 1, and μ is a vector of length 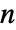 with positive elements.
with positive elements. - ContinuousMarkovProcess can be used with such functions as MarkovProcessProperties, PDF, Probability, and RandomFunction.
Background & Context
- ContinuousMarkovProcess constructs a continuous Markov process, i.e. a continuous-time process with a finite number of states such that the probability of transitioning to a given state depends only on the current state. More precisely, processes defined by ContinuousMarkovProcess consist of states whose values come from a finite set and for which the time spent in each state has an exponential distribution. Processes defined by ContinuousMarkovProcess are sometimes referred to as continuous-time Markov chains (CTMC) and are the continuous analogues of processes constructed by DiscreteMarkovProcess, the time parameters of which are discrete.
- Continuous Markov processes arise naturally in many areas of mathematics and physical sciences and are used to model queues, chemical reactions, electronics failures, and geological sedimentation. In addition, a considerable amount of research has gone into the understanding of continuous Markov processes from a probability theoretic perspective.
- A number of parameter schemes may be input into ContinuousMarkovProcess. Most typically, ContinuousMarkovProcess constructs a CTMC from input parameters that specify an initial state and a transition rate matrix
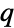 . The initial state may be a single integer
. The initial state may be a single integer 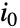 between 1 and
between 1 and 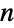 or a probability vector
or a probability vector 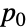 of length
of length 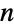 consisting of non-negative elements that sum to 1. The transition rate matrix
consisting of non-negative elements that sum to 1. The transition rate matrix 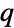 is a square matrix (or SparseArray) of dimension
is a square matrix (or SparseArray) of dimension 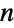 ×
×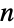 whose rows sum to 0 and which satisfies
whose rows sum to 0 and which satisfies 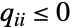 and
and 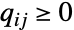 for
for 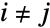 , and the states of ContinuousMarkovProcess are integers between 1 and
, and the states of ContinuousMarkovProcess are integers between 1 and 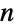 . The time
. The time 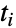 for which a given ContinuousMarkovProcess stays in state
for which a given ContinuousMarkovProcess stays in state 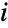 before transitioning to state
before transitioning to state 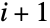 is distributed according to an exponential distribution, i.e. tiExponentialDistribution[-qi i], where
is distributed according to an exponential distribution, i.e. tiExponentialDistribution[-qi i], where 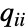 denotes the
denotes the 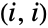 -entry of
-entry of 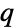 and
and 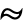 is a shorthand for Distributed.
is a shorthand for Distributed. - A ContinuousMarkovProcess may also be specified using a transition matrix
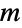 together with associated transition rates
together with associated transition rates 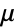 . In this case, the entries
. In this case, the entries 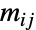 of
of 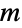 consist of conditional transition probabilities, i.e. the probability that
consist of conditional transition probabilities, i.e. the probability that 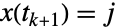 given that
given that 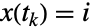 , and the associated transition rate
, and the associated transition rate 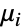 specifies that the time between events in state
specifies that the time between events in state 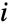 is distributed according to ExponentialDistribution[μi]. Here,
is distributed according to ExponentialDistribution[μi]. Here, 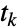 is defined to be the random time at which the
is defined to be the random time at which the 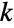
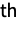 state transition has occurred,
state transition has occurred, 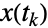 denotes the state transitioned to by the process at time
denotes the state transitioned to by the process at time 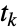 ,
, 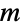 is an
is an 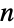 ×
×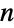 matrix with non-negative elements and rows that sum to 1, and
matrix with non-negative elements and rows that sum to 1, and 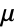 is a vector of length
is a vector of length 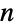 with positive elements.
with positive elements. - Finally, ContinuousMarkovProcess can produce a CTMC from an input graph
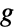 with edges
with edges 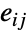 denoting the transition rates between the events represented by the vertices
denoting the transition rates between the events represented by the vertices 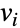 and
and 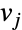 .
. - A number of functions can be used with ContinuousMarkovProcess, including MarkovProcessProperties, PDF, and Probability. RandomFunction can be used to simulate a CTMC, the result of which (a TemporalData object) may then be visualized via ListLinePlot, sliced via TimeSeries, and analyzed by way of functions like Mean, Variance, StandardDeviation, and Moment—functions that can also be used to analyze distributions defined by ContinuousMarkovProcess. ContinuousMarkovProcess can also be input as the mproc parameter to FirstPassageTimeDistribution in order to analyze the distribution of times required for a CTMC to pass from its initial state to its final state for the first time, while the statistical properties of processes constructed by ContinuousMarkovProcess can be analyzed directly using functions such as CharacteristicFunction and CentralMomentGeneratingFunction.
- In addition to their statistical properties, processes constructed by ContinuousMarkovProcess can be represented as graphs via Graph, thus inheriting a level of graph-theoretic functionality. Functions such as QueueingProcess, QueueProperties, and SurvivalFunction make use of properties of CTMC in modeling and applications. ContinuousMarkovProcess may also serve as an approximation tool by way of EstimatedProcess, a function that computes an approximate CTMC with
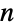 states which best fits a given dataset.
states which best fits a given dataset.
Examples
open all close allBasic Examples (2)
Scope (12)
Visualize the process as a graph, with the transition rates given as tooltips:
Convert the graph representation back to a continuous Markov process:
Find the recurrent and transient classes for a continuous Markov process:
Generate a sample path with default machine precision:
Generate a sample path with higher precision:
Estimate the process parameters from sample data:
Find the distribution for the time to absorption:
Compare with the value obtained from process simulation:
Compute the probability of an event:
Find the stationary distribution:
Perform operations on the stationary distribution:
Find the conditional mean number of total transitions starting in state 1 and ending in state 4:
Compare with the results from simulation:
Find the conditional mean number of transitions from state 2 to state 3:
Generalizations & Extensions (2)
Applications (9)
Boston-to-Cambridge migration rate is estimated to be six people per year:
Find the percentage of people who moved in a period of two months:
A hospital owns two identical and independent power generators. The time to breakdown for each is exponential with parameter ![]() , and the time for repair of a malfunctioning generator is exponential with parameter
, and the time for repair of a malfunctioning generator is exponential with parameter ![]() . Assuming both generators were in order at
. Assuming both generators were in order at ![]() , find the probability that both generators remain functional at time
, find the probability that both generators remain functional at time ![]() . The number of working generators can be modeled with a continuous-time Markov chain, with the state number representing 1 plus the number of working generators:
. The number of working generators can be modeled with a continuous-time Markov chain, with the state number representing 1 plus the number of working generators:
A flammable product is stored in a special tank at a filling station. Customers asking for the product arrive according to a Poisson process with rate ![]() . Each customer asks for one unit of the product. Any demand that occurs when the tank is out of stock is lost. Opportunities to replenish the stock in the tank occur according to a Poisson process with rate
. Each customer asks for one unit of the product. Any demand that occurs when the tank is out of stock is lost. Opportunities to replenish the stock in the tank occur according to a Poisson process with rate ![]() . The two Poisson processes are assumed to be independent of each other. For reasons of security, the stock can only be replenished when the tank is empty. At those opportunities, the stock is replenished with
. The two Poisson processes are assumed to be independent of each other. For reasons of security, the stock can only be replenished when the tank is empty. At those opportunities, the stock is replenished with ![]() units:
units:
Long-run average stock in the tank:
Long-run fraction of demand that is lost:
A router receives packets from a group of users and transmits them over a single transmission line. Suppose packets arrive according to a Poisson process at a rate of one packet every 4 milliseconds and packet transmission times are exponentially distributed with mean 3 milliseconds. Approximate an infinite router capacity:
Probability that there are more than five packets waiting for transmission in the router:
The number of flaws appearing on a polished mirror surface is a Poisson random variable. For a mirror with an area of ![]() , the probability of no flaws is 0.91. Find the probability of no flaws on the surface of another mirror with an area of
, the probability of no flaws is 0.91. Find the probability of no flaws on the surface of another mirror with an area of ![]() , fabricated using the same process:
, fabricated using the same process:
The arrival pattern of cars to an oil change center follows a Poisson process at the rate of four per hour. There is a single available mechanic, and the time taken to perform an oil change is exponentially distributed and requires an average of 12 minutes to carry out. Approximate an unlimited car space:
Simulate the number of cars in the queue:
The probability that there are more than three cars in the queue:
Mean and variance for the number of cars in the system:
Distribution for the number of cars in the system:
Vehicles in a certain country are required to be assessed every year for roadworthiness. At one vehicle assessment center, drivers wait for an average of 15 minutes before the roadworthiness assessment of their vehicle commences. The assessment takes on average 20 minutes to complete. Following the assessment, 80% of vehicles are passed as roadworthy, allowing the driver to drive home. A further 15% of vehicles are categorized as a "minor fail"; these vehicles require on average 30 minutes of repair work before the driver is allowed to drive home. The remaining 5% of vehicles are categorized as a "significant fail"; these vehicles require on average three hours of repair work before the driver can go home. Model the operation of the vehicle assessment center using a continuous-time Markov model, with states W (waiting for assessment), A (assessment taking place), M (minor repair taking place), S (significant repair taking place), and H (traveling home):
Make the row sums zero by setting diagonals to the negative sum of off-diagonal elements:
Process for modeling assessment and repair:
Probability that a vehicle is undergoing significant repair at time ![]() :
:
Average time in minutes spent by vehicles in assessment and repair:
Consider a system with exponential interarrival and service times. There is one server and room for two customers: the one in service and another that is waiting. Let the number of customers in the room at time ![]() be
be ![]() . This is an M/M/1/2 queue; model it as a birth-death process with the following transition rate matrix, where the states are indexed as
. This is an M/M/1/2 queue; model it as a birth-death process with the following transition rate matrix, where the states are indexed as ![]() :
:
The transition rate matrix is irreducible:
Hence the stationary distribution exists uniquely:
This agrees with the stationary distribution for QueueingProcess:
It is a truncated geometric distribution:
Fraction of time the server is busy:
This agrees with the result from QueueProperties:
Average number of customers in the room in the long run:
Proportion of potential customers that enter the room in the long run:
Increase in number of customers if the server works twice as fast:
The Hubble space telescope carries six gyroscopes, with a minimum of three required for full accuracy. The operating times of the gyroscopes are independent and exponentially distributed with failure rate ![]() . If a fourth gyroscope fails, the telescope goes into sleep mode, in which further observations are suspended. It requires an exponential time with mean 1/
. If a fourth gyroscope fails, the telescope goes into sleep mode, in which further observations are suspended. It requires an exponential time with mean 1/![]() to put the telescope into sleep mode, after which the base station on Earth receives a sleep signal, and a shuttle mission is prepared. It takes an exponential time with mean 1/
to put the telescope into sleep mode, after which the base station on Earth receives a sleep signal, and a shuttle mission is prepared. It takes an exponential time with mean 1/![]() before the repair crew arrives at the telescope and repairs the stabilizing unit with the gyroscopes. In the meantime, the other two gyroscopes may fail. If the last gyroscope fails, the telescope will crash. Suppose
before the repair crew arrives at the telescope and repairs the stabilizing unit with the gyroscopes. In the meantime, the other two gyroscopes may fail. If the last gyroscope fails, the telescope will crash. Suppose ![]() ,
, ![]() , and
, and ![]() , all with units of inverse years:
, all with units of inverse years:
Visualize the process, with integers representing the number of operational gyroscopes:
Find the probability that the telescope will crash in the next 10 years:
Find the probability that sleep mode is not reached (no shuttle mission is required) in 10 years:
Properties & Relations (1)
Related Guides
Text
Wolfram Research (2012), ContinuousMarkovProcess, Wolfram Language function, https://reference.wolfram.com/language/ref/ContinuousMarkovProcess.html (updated 2014).
CMS
Wolfram Language. 2012. "ContinuousMarkovProcess." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2014. https://reference.wolfram.com/language/ref/ContinuousMarkovProcess.html.
APA
Wolfram Language. (2012). ContinuousMarkovProcess. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ContinuousMarkovProcess.html
BibTeX
@misc{reference.wolfram_2025_continuousmarkovprocess, author="Wolfram Research", title="{ContinuousMarkovProcess}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/ContinuousMarkovProcess.html}", note=[Accessed: 08-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_continuousmarkovprocess, organization={Wolfram Research}, title={ContinuousMarkovProcess}, year={2014}, url={https://reference.wolfram.com/language/ref/ContinuousMarkovProcess.html}, note=[Accessed: 08-January-2026]}