CopulaDistribution[ker,{dist1,dist2,…}]
represents a copula distribution with kernel distribution ker and marginal distributions dist1, dist2, … .


CopulaDistribution
CopulaDistribution[ker,{dist1,dist2,…}]
represents a copula distribution with kernel distribution ker and marginal distributions dist1, dist2, … .
Details


- The cumulative distribution function is given by
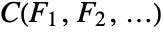 , where
, where 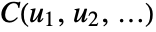 is the CDF for the kernel ker, and
is the CDF for the kernel ker, and 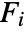 is the CDF for disti.
is the CDF for disti. - Marginal distribution disti can be any univariate distribution.
- The following kernels ker can be used:
-
"Product" 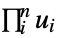
independent distributions "Maximal" 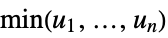
Frechét–Hoeffding upper bound "Minimal" 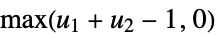
Frechét–Hoeffding lower bound {"Frank",α} 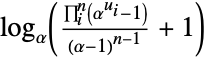
Frank copula {"Clayton",c} 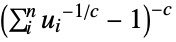
Clayton–Pareto copula {"GumbelHougaard",α} 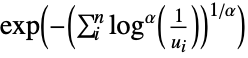
Gumbel–Hougaard copula {"FGM",α} 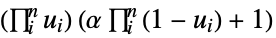
Farlie–Gumbel–Morgenstern copula {"AMH",α} 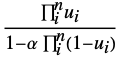
Ali–Mikhail–Haq copula {"Binormal",ρ} 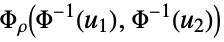
bivariate Gaussian with correlation 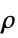
{"Multinormal",Σ} 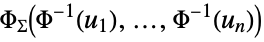
multivariate Gaussian with covariance 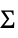
{"MultivariateT",Σ,ν} 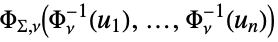
multivariate 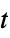 -distribution with scale matrix
-distribution with scale matrix 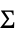 and
and 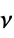 degrees of freedom
degrees of freedom - For "Frank",
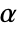 can be any positive number in two dimensions and any positive number less than or equal to a certain constant
can be any positive number in two dimensions and any positive number less than or equal to a certain constant 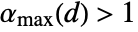 for dimensions higher than two.
for dimensions higher than two. - For "Clayton",
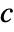 can be any positive number.
can be any positive number. - For "GumbelHougaard",
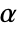 can be any real number greater than or equal to 1.
can be any real number greater than or equal to 1. - For "FGM" and "AMH",
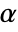 can be any real number between
can be any real number between 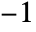 and
and 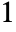 .
. - The parameters for "Binormal", "Multinormal", and "MultivariateT" are the same as for BinormalDistribution, MultinormalDistribution, and MultivariateTDistribution, respectively.
- CopulaDistribution can be used with such functions as Mean, PDF, and RandomVariate, etc.
Background & Context
- CopulaDistribution[ker,{dist1,dist2,…,distn}] represents a multivariate statistical distribution whose
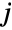
 marginal distribution (MarginalDistribution) is precisely distj, and for which the CDF of a distj-distributed random variate follows a uniform distribution (UniformDistribution). For a general copula distribution CopulaDistribution[ker,{dist1,dist2,…,distn}], the probability density function (PDF) of Yj=TransformedDistribution[Fj[x],xdistj] is equivalent to UniformDistribution[] whenever Fj[x] is the CDF of distj. While all copula distributions share the above properties, the characteristics and behavior of a specific copula distribution depend both on its kernel ker and on its marginals dist1,dist2,…,distn.
marginal distribution (MarginalDistribution) is precisely distj, and for which the CDF of a distj-distributed random variate follows a uniform distribution (UniformDistribution). For a general copula distribution CopulaDistribution[ker,{dist1,dist2,…,distn}], the probability density function (PDF) of Yj=TransformedDistribution[Fj[x],xdistj] is equivalent to UniformDistribution[] whenever Fj[x] is the CDF of distj. While all copula distributions share the above properties, the characteristics and behavior of a specific copula distribution depend both on its kernel ker and on its marginals dist1,dist2,…,distn. - In practice, a copula is a tool that describes dependence between variables, and in this context, varying ker allows investigation of different degrees of dependence (for example, {"FGM",α} best models weak variable dependence, whereas "Product" allows analysis of independent variables). There are 11 predefined kernels ker that may be used to parametrize a copula distribution. These 11 can be split into roughly four groups, consisting of the independence-dependence kernels ("Product", "Maximal", and "Minimal"); the Archimedean kernels ({"Frank",α}, where
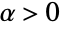 for
for 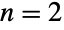 and
and 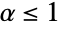 for
for 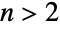 , {"Clayton",c} for
, {"Clayton",c} for 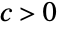 , {"GumbelHougaard",α} for
, {"GumbelHougaard",α} for 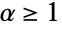 , and {"AMH",α} for
, and {"AMH",α} for 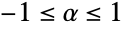 ); the distribution-derived kernels ({"Binormal",ρ} for ρ as in BinormalDistribution, {"Multinormal",Σ} for Σ as in MultinormalDistribution, and {"MultivariateT",Σ,ν} for Σ, ν as in MultivariateTDistribution); and the non-associative kernels ({"FGM",α} for
); the distribution-derived kernels ({"Binormal",ρ} for ρ as in BinormalDistribution, {"Multinormal",Σ} for Σ as in MultinormalDistribution, and {"MultivariateT",Σ,ν} for Σ, ν as in MultivariateTDistribution); and the non-associative kernels ({"FGM",α} for 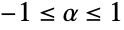 ), members of which share similar qualitative or theoretical properties.
), members of which share similar qualitative or theoretical properties. - Sklar's theorem proves the existence of a copula
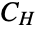 that "couples" any joint distribution
that "couples" any joint distribution 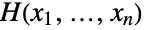 with its univariate marginals
with its univariate marginals  via the relation
via the relation 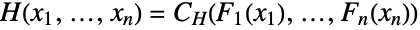 and thus demonstrates that copula distributions are ubiquitous in multivariate statistics. Copula distributions date as far back as the 1940s, though much of the terminology and machinery used today were developed in the 1950s and 1960s. Since their inception, copulas have been used to model phenomena in areas including reliability theory, meteorology, and queueing theory, while specially purposed copulas and kernels have been developed to serve as tools in fields such as survival analysis (via survival copulas) and mathematical finance (via panic copulas). Copula distributions are also of independent theoretical interest in Monte Carlo theory and applied mathematics.
and thus demonstrates that copula distributions are ubiquitous in multivariate statistics. Copula distributions date as far back as the 1940s, though much of the terminology and machinery used today were developed in the 1950s and 1960s. Since their inception, copulas have been used to model phenomena in areas including reliability theory, meteorology, and queueing theory, while specially purposed copulas and kernels have been developed to serve as tools in fields such as survival analysis (via survival copulas) and mathematical finance (via panic copulas). Copula distributions are also of independent theoretical interest in Monte Carlo theory and applied mathematics. - Many relationships exist between CopulaDistribution[ker,{dist1,…,distn}] and various other distributions depending on the parameters ker and distj. CopulaDistribution["Product",{dist1,…,distn}] is equivalent to ProductDistribution[dist1,…,distn] for all distributions distj, and so the product copula of two instances of NormalDistribution is BinormalDistribution. In addition, the product copula is equivalent to the binormal copula with zero correlation in the sense that the PDF of CopulaDistribution["Product",{dist1,…,distn}] is precisely the same as that of CopulaDistribution[{"Binormal",0},{dist1,…,distn}] for all distributions distj. Among distribution-derived kernels, a binormal copula with NormalDistribution marginals and a multivariate
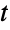 -copula with StudentTDistribution marginals are equivalent to BinormalDistribution and MultivariateTDistribution, respectively, while a practically limitless number of qualitatively similar relationships exist between Archimedean copulas and miscellaneous distributions.
-copula with StudentTDistribution marginals are equivalent to BinormalDistribution and MultivariateTDistribution, respectively, while a practically limitless number of qualitatively similar relationships exist between Archimedean copulas and miscellaneous distributions.
Examples
open all close allBasic Examples (3)
Scope (32)
Basic Uses (6)
Define a product copula using two normal distributions:
Cumulative distribution function:
Define a Frank copula using two uniform distributions:
Define an FGM copula with beta distributions:
Moment and moment-generating function:
Define a maximal copula with discrete components:
Compute probabilities and expectations:
Define a minimal copula with Poisson distributions:
Copula Kernels (11)
Cumulative distribution function:
Cumulative distribution function:
Cumulative distribution function:
Cumulative distribution function:
Cumulative distribution function:
Cumulative distribution function:
A Farlie–Gordon–Morgenstern copula:
Cumulative distribution function:
Cumulative distribution function:
Parametric Distributions (4)
Define a minimal copula with beta distributions as marginals:
Cumulative distribution function:
Define a maximal copula with different continuous marginals:
Cumulative distribution function:
Define a copula with Poisson marginal distributions:
Define a copula with negative binomial distribution marginals:
Nonparametric Distributions (3)
Define a copula with SmoothKernelDistribution:
Define a copula with EmpiricalDistribution:
Define a copula with a HistogramDistribution:
Derived Distributions (8)
Define a copula distribution with a TruncatedDistribution as a marginal:
Define a copula distribution with a CensoredDistribution as a marginal:
Define a copula with a MixtureDistribution as a marginal:
Cumulative distribution function:
Define a copula with a ParameterMixtureDistribution as a marginal:
Define a copula with an OrderDistribution as a marginal:
Cumulative distribution function:
Define a copula with a TransformedDistribution as a marginal:
Define a copula with a MarginalDistribution as a marginal:
Copula with QuantityDistribution marginals evaluates to QuantityDistribution:
Applications (6)
A system is composed of four components, each with lifespan exponentially distributed with parameter ![]() per hour. Dependencies in the time to failure are modeled by a Farlie–Gumbel–Morgenstern copula with α1/3. Find the probability that no component fails before 500 hours:
per hour. Dependencies in the time to failure are modeled by a Farlie–Gumbel–Morgenstern copula with α1/3. Find the probability that no component fails before 500 hours:
Find the probability that one component will fail after 1000 hours:
Assume the values of two assets follow a geometric Brownian motion with drifts ![]() and
and ![]() and volatilities
and volatilities ![]() and
and ![]() , respectively. Assuming both initial values to be 1, find the bounds for the joint cumulative distribution function of both assets at time
, respectively. Assuming both initial values to be 1, find the bounds for the joint cumulative distribution function of both assets at time ![]() :
:
Assuming the values below compare the plots of the CDFs:
Two firms have debts ![]() and
and ![]() and initial assets both equal to 1. Assume the values of the assets follow a geometric Brownian motion with drifts
and initial assets both equal to 1. Assume the values of the assets follow a geometric Brownian motion with drifts ![]() and
and ![]() and volatilities
and volatilities ![]() and
and ![]() , respectively. Find the joint probability of the default at time
, respectively. Find the joint probability of the default at time ![]() assuming a Frank copula:
assuming a Frank copula:
Default probability depending on α:
A Cauchy copula is a multivariate Student ![]() copula with one degree of freedom:
copula with one degree of freedom:
Visualize the density using a scatter plot:
Define a Gumbel–Hougaard copula for different values of the parameter:
Show how the value of the parameter influences the dependence between values:
Gumbel's bivariate logistic distribution is an AMH copula with logistic marginal distributions:
Visualize its probability density function:
Cumulative distribution function has the structure of CDF of the univariate logistic distribution:
Properties & Relations (5)
The product copula distribution of two normal distributions is a binormal distribution:
Product copula is equivalent to binormal copula with zero correlation:
Binormal copula with normal marginals is a BinormalDistribution:
Multivariate ![]() copula with Student
copula with Student ![]() marginals is a MultivariateTDistribution:
marginals is a MultivariateTDistribution:
MarginalDistribution of a copula returns the component distributions:
Possible Issues (1)
CopulaDistribution will not accept ProductDistribution as a marginal:
The correct syntax is to enter all the distributions in the list:
See Also
MarginalDistribution UniformDistribution ProductDistribution BinormalDistribution MultinormalDistribution MultivariateTDistribution
Function Repository: MutualInformation
Related Guides
Text
Wolfram Research (2010), CopulaDistribution, Wolfram Language function, https://reference.wolfram.com/language/ref/CopulaDistribution.html (updated 2016).
CMS
Wolfram Language. 2010. "CopulaDistribution." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/CopulaDistribution.html.
APA
Wolfram Language. (2010). CopulaDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/CopulaDistribution.html
BibTeX
@misc{reference.wolfram_2025_copuladistribution, author="Wolfram Research", title="{CopulaDistribution}", year="2016", howpublished="\url{https://reference.wolfram.com/language/ref/CopulaDistribution.html}", note=[Accessed: 09-March-2026]}
BibLaTeX
@online{reference.wolfram_2025_copuladistribution, organization={Wolfram Research}, title={CopulaDistribution}, year={2016}, url={https://reference.wolfram.com/language/ref/CopulaDistribution.html}, note=[Accessed: 09-March-2026]}