BinormalDistribution
BinormalDistribution[{μ1,μ2},{σ1,σ2},ρ]
represents a bivariate normal distribution with mean {μ1,μ2} and covariance matrix {{σ12,ρ σ1 σ2},{ρ σ1 σ2,σ22}}.
BinormalDistribution[{σ1,σ2},ρ]
represents a bivariate normal distribution with zero mean.
represents a bivariate normal distribution with zero mean and covariance matrix {{1,ρ },{ρ,1}}.
Details
- The probability density for vector
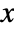 in a binormal distribution is proportional to
in a binormal distribution is proportional to 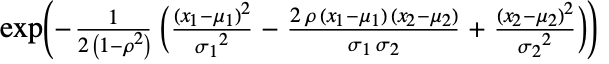 .
. - BinormalDistribution allows μi to be any real numbers, σi any positive real numbers, and ρ any number between -1 and 1.
- BinormalDistribution allows μi and σi to be quantities with the same unit dimensions componentwise, and ρ to be a dimensionless quantity. »
- BinormalDistribution can be used with such functions as Mean, CDF, and RandomVariate.
Background & Context
- BinormalDistribution[{μ1,μ2},{σ1,σ2},ρ] represents a bivariate (i.e. two-variable) statistical distribution defined over pairs of real numbers with the property that each of the first and second marginal distributions (MarginalDistribution) is NormalDistribution, i.e. the variables
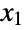 and
and 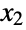 satisfy x1NormalDistribution[μ1,σ1] and x2NormalDistribution[μ2,σ2], respectively. The binormal distribution is therefore parametrized by a pair of real numbers (μ1,μ2) called the mean vector, a pair of positive real numbers (σ1,σ2) called the standard deviation vector, and a real number
satisfy x1NormalDistribution[μ1,σ1] and x2NormalDistribution[μ2,σ2], respectively. The binormal distribution is therefore parametrized by a pair of real numbers (μ1,μ2) called the mean vector, a pair of positive real numbers (σ1,σ2) called the standard deviation vector, and a real number 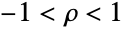 known as the correlation of
known as the correlation of 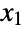 and
and 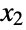 . ρ is used to define the associated covariance matrix
. ρ is used to define the associated covariance matrix 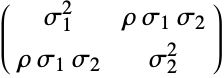 of the distribution, i.e. the 2×2 matrix whose
of the distribution, i.e. the 2×2 matrix whose 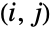
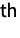 entry is the covariance between the variables
entry is the covariance between the variables 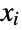 and
and 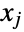 .
. - The two-argument form BinormalDistribution[{σ1,σ2},ρ] is equivalent to BinormalDistribution[{0,0},{σ1,σ2},ρ], while the one-argument form BinormalDistribution[ρ] is equivalent to BinormalDistribution[{0,0},{1,1},ρ] and is sometimes referred to as the standard binormal distribution. Random variables that are binormally distributed are sometimes called binormal variates. The binormal distribution is sometimes referred to as the bivariate normal distribution, and the standard binormal distribution may also be referred to as the unit binormal distribution.
- The probability density function (PDF) of a binormal distribution has an absolute maximum at the mean
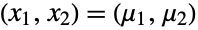 though, unlike the univariate normal distribution, it may have multiple "peaks". In general, the tails of each of the associated marginal PDFs are "thin" in the sense that the marginal PDF decreases exponentially for large values of
though, unlike the univariate normal distribution, it may have multiple "peaks". In general, the tails of each of the associated marginal PDFs are "thin" in the sense that the marginal PDF decreases exponentially for large values of 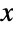 . (This behavior can be made quantitatively precise by analyzing the SurvivalFunction of these distributions.)
. (This behavior can be made quantitatively precise by analyzing the SurvivalFunction of these distributions.) - The PDF
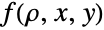 of the binormal distribution is unique in the sense that it satisfies the particular partial differential equation
of the binormal distribution is unique in the sense that it satisfies the particular partial differential equation 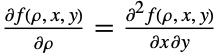 . Unlike the PDF of a univariate normal distribution, which is "bell-shaped" (in the two-dimensional sense), the PDF of a binormal distribution may or may not be "bell-shaped" (in the three-dimensional sense). In particular, the overall shape of the PDF of a binormal distribution may look significantly different than that of a normal distribution, depending on the covariance of the two variables. In general, the PDF corresponding to values of ρ near zero tends to look more "uniform" (i.e. bell-shaped in the 3D sense) while values near
. Unlike the PDF of a univariate normal distribution, which is "bell-shaped" (in the two-dimensional sense), the PDF of a binormal distribution may or may not be "bell-shaped" (in the three-dimensional sense). In particular, the overall shape of the PDF of a binormal distribution may look significantly different than that of a normal distribution, depending on the covariance of the two variables. In general, the PDF corresponding to values of ρ near zero tends to look more "uniform" (i.e. bell-shaped in the 3D sense) while values near 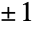 generally correspond to functions that look "rocky" or "spikey". The parameters σ1 and σ2 determine the "thickness" of the tails of the associated one-dimensional PDF and, together with ρ, contribute to a number of qualitative properties of the bivariate PDF, including its height and its number of "peaks".
generally correspond to functions that look "rocky" or "spikey". The parameters σ1 and σ2 determine the "thickness" of the tails of the associated one-dimensional PDF and, together with ρ, contribute to a number of qualitative properties of the bivariate PDF, including its height and its number of "peaks". - The binormal distribution came to prominence through the work of English polymath Francis Galton in the late 1880s, who used it to explain generational variation issues mentioned in the work of Charles Darwin. However, the properties of the distribution had already been studied by Irish-American mathematician Robert Adrain and French mathematician Pierre-Simon Laplace as early as 1808. Binormal distributions occur widely in a number of areas. In Bayesian analysis, the conjugate priors of the mean vector and the covariance matrix are a binormal distribution and an inverse Wishart distribution, respectively. The binormal distribution can be used to examine the relationship between any pair of normally distributed variables, and due to the multitude of applications of the normal distribution, the binormal distribution is used to model a number of physical phenomena. For example, the binormal distribution is sometimes used to model rainfall in adjacent geographical regions in order to examine its effect on agriculture. Moreover, a number of physical attributes, including height, weight, shoe size, etc., are known to be well approximated in populations by the normal distribution, whereby it follows that the binormal distribution can be used to study these pairs of properties when observed in the same individual. Other applications of the binormal distribution have been found in areas such as computer graphics, manufacturing and quality management, and meteorology.
- RandomVariate can be used to give one or more machine- or arbitrary-precision (the latter via the WorkingPrecision option) pseudorandom variates from a binormal distribution. Distributed[{x,y},BinormalDistribution[{μ1,μ2},{σ1,σ2},ρ]], written more concisely as {x,y}BinormalDistribution[{μ1,μ2},{σ1,σ2},ρ], can be used to assert that a pair (x,y) of random variables is distributed according to a binormal distribution. Such an assertion can then be used in functions such as Probability, NProbability, Expectation, and NExpectation.
- The probability density and cumulative distribution functions may be given using PDF[BinormalDistribution[{μ1,μ2},{σ1,σ2},ρ],{x,y}] and CDF[BinormalDistribution[{μ1,μ2},{σ1,σ2},ρ],{x,y}]. The mean, median, variance, raw moments, and central moments may be computed using Mean, Median, Variance, Moment, and CentralMoment, respectively.
- DistributionFitTest can be used to test if a given dataset is consistent with a binormal distribution, EstimatedDistribution to estimate a binormal parametric distribution from given data, and FindDistributionParameters to fit data to a binormal distribution. ProbabilityPlot can be used to generate a plot of the CDF of given data against the CDF of a symbolic binormal distribution and QuantilePlot to generate a plot of the quantiles of given data against the quantiles of a symbolic binormal distribution.
- TransformedDistribution can be used to represent a transformed binormal distribution, CensoredDistribution to represent the distribution of values censored between upper and lower values, and TruncatedDistribution to represent the distribution of values truncated between upper and lower values. CopulaDistribution can be used to build higher-dimensional distributions that contain a binormal distribution, and ProductDistribution can be used to compute a joint distribution with independent component distributions involving binormal distributions.
- BinormalDistribution is closely related to a number of other distributions. By definition, BinormalDistribution is the two-variable extension of NormalDistribution and hence can be viewed as a specific case of MultinormalDistribution. BinormalDistribution is a limiting distribution for MultivariateTDistribution in the sense that the PDF of MultivariateTDistribution[{{1,ρ},{ρ,1}},ν] as ν tends to Infinity is precisely the PDF of BinormalDistribution[{0,0},{1,1},ρ]. In addition, BinormalDistribution can be transformed to give both SkewNormalDistribution and LogMultinormalDistribution and can be viewed as a building block of HoytDistribution in the sense that the norm of a binormally distributed vector with mean vector (0,0) and standard deviation vector
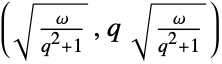 is distributed according to HoytDistribution[q,ω]. BinormalDistribution can be obtained from NormalDistribution by way of a product CopulaDistribution and is also related to RayleighDistribution, RiceDistribution, and BeckmannDistribution.
is distributed according to HoytDistribution[q,ω]. BinormalDistribution can be obtained from NormalDistribution by way of a product CopulaDistribution and is also related to RayleighDistribution, RiceDistribution, and BeckmannDistribution.
Examples
open allclose allBasic Examples (4)
Scope (8)
Generate a sample of pseudorandom vectors from a binormal distribution:
Visualize the sample using a histogram:
Distribution parameters estimation:
Estimate the distribution parameters from sample data:
Skewness and kurtosis are constant vectors:
Correlation of a standard binormal distribution:
Different mixed moments for a standard binormal distribution:
Closed form for a symbolic order:
Marginal distributions are normal:
Consistent use of Quantity in parameters yields QuantityDistribution:
Find the fraction of population with body mass index above a threshold:
Applications (5)
Show a distribution function and its histogram in the same plot:
Compare the PDF to its histogram version:
Compare the CDF to its histogram version:
Specify BinormalDistribution model for measurements of both air pressure and volume using Quantity parameters:
Compute distribution for the amount of air in the room at room temperature:
Find the mean and the standard deviation:
The average city and highway mileage for midsize cars follows a binormal distribution:
Find the percentage of midsize cars with at least 19 mpg in the city and at least 26 mpg on the highway:
Find the average highway mileage for cars with city mileage of 15 mpg or less:
Show the distribution of city and highway mileage:
Find the mileage, assuming 65% of the driving is done in the city:
Cylindrical roller bearings are produced to have a diameter of 6 cm and a length of 10 cm. Quality control allows the diameter and the length to vary normally, with standard deviation of 0.01 cm. It is also known that longer length corresponds to shorter diameter and vice versa, with a correlation coefficient of ![]() . Use BinormalDistribution to model the volume of the bearings:
. Use BinormalDistribution to model the volume of the bearings:
Illustrate the volume probability density function estimated from the sample:
Two prides of lions hunt on the same territory for prey. The weekly takings of both prides follow BinormalDistribution with means ![]() and
and ![]() and variances
and variances ![]() and
and ![]() . Because they compete for food, their weekly takings are negatively correlated, say
. Because they compete for food, their weekly takings are negatively correlated, say ![]() . Assuming both prides together hunted
. Assuming both prides together hunted ![]() kg of prey, estimate individual prides' shares as a function of catch size
kg of prey, estimate individual prides' shares as a function of catch size ![]() :
:
Find the expected value for the amount caught by the first pride:
The share of the first pride is smaller despite higher expectation and smaller variance when the size of the combined catch is larger than the sum of means:
Find the share for the specified numbers for negative correlation and for zero correlation:
Properties & Relations (17)
Equal probability contours for a binormal distribution:
The binormal distribution is closed under affine transformation:
The binormal PDF ![]() satisfies the PDE
satisfies the PDE ![]() :
:
Hence the CDF ![]() satisfies
satisfies ![]() and integrates both sides wrt
and integrates both sides wrt ![]() :
:
Binormal distribution shows regression toward the mean for ![]() :
:
Relationships to other distributions:
The conditional distribution of a binormal distribution is a NormalDistribution:
The conditional distribution differs from marginal distribution when ![]() :
:
Each bivariate marginal of MultinormalDistribution has binormal distribution:
Binormal distribution is the two-dimensional case of MultinormalDistribution:
Binormal distribution is the limit of a two-dimensional MultivariateTDistribution as ![]() goes to
goes to ![]() :
:
LogMultinormalDistribution is a transformation of BinormalDistribution:
Binormal distribution is related to BeckmannDistribution:
Binormal distribution is related to RiceDistribution:
Binormal distribution is related to RayleighDistribution:
HoytDistribution can be obtained from binormal distribution:
SkewNormalDistribution is a transformation of BinormalDistribution:
The product CopulaDistribution of two normal distributions is a binormal distribution:
A CopulaDistribution with a binormal subkernel and normal marginals is binormal:
Text
Wolfram Research (2010), BinormalDistribution, Wolfram Language function, https://reference.wolfram.com/language/ref/BinormalDistribution.html (updated 2016).
CMS
Wolfram Language. 2010. "BinormalDistribution." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/BinormalDistribution.html.
APA
Wolfram Language. (2010). BinormalDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/BinormalDistribution.html