LogMultinormalDistribution
LogMultinormalDistribution[μ,Σ]
represents a log-multinormal distribution with parameters μ and Σ.
Details
- LogMultinormalDistribution[μ,Σ] is equivalent to TransformedDistribution[Exp[{u1,u2,…,un}],{u1,u2,…,un}MultinormalDistribution[μ,Σ]].
- LogMultinormalDistribution allows μ to be any vector of real numbers, and Σ any symmetric positive definite
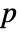 ×
×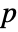 matrix of real numbers with p=Length[μ].
matrix of real numbers with p=Length[μ].
Background & Context
- LogMultinormalDistribution[μ,Σ] represents a continuous multivariate statistical distribution supported over the subset of
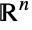 consisting of all tuples
consisting of all tuples 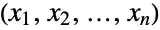 satisfying
satisfying 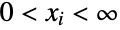 and characterized by the property that each of the
and characterized by the property that each of the 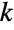
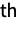 marginal distributions is log-normal for
marginal distributions is log-normal for 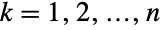 . In other words, each of the variables
. In other words, each of the variables 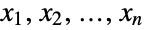 satisfies xkLogNormalDistribution for
satisfies xkLogNormalDistribution for 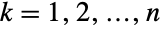 . The log-multinormal distribution LogMultinormalDistribution[μ,Σ] is parametrized by a vector μ of real numbers and by a positive definite symmetric matrix Σ that satisfy nLength[μ]Length[Σ] and that define the associated mean, variance, and covariance of the distribution.
. The log-multinormal distribution LogMultinormalDistribution[μ,Σ] is parametrized by a vector μ of real numbers and by a positive definite symmetric matrix Σ that satisfy nLength[μ]Length[Σ] and that define the associated mean, variance, and covariance of the distribution. - The log-multinormal distribution is sometimes referred to as the log multivariate normal distribution, a reference to the fact that the log-multinormal distribution is precisely the distribution of the random variate vector
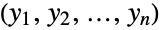 whose coordinates are random variates satisfying
whose coordinates are random variates satisfying 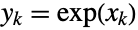 for
for 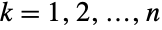 and where the vector
and where the vector 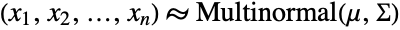 . Similarly, since the vector
. Similarly, since the vector 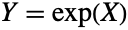 is log-multinormally distributed given a vector
is log-multinormally distributed given a vector 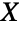 that is multinormally distributed, the distribution is sometimes referred to as the multivariate log-normal distribution. Though probability density function (PDF) of a log-multinormal distribution has an absolute maximum, it may have multiple "peaks" (i.e. relative maxima). In general, the tails of each of the associated marginal PDFs are "fat" in the sense that the marginal PDF decreases algebraically rather than exponentially for large values of
that is multinormally distributed, the distribution is sometimes referred to as the multivariate log-normal distribution. Though probability density function (PDF) of a log-multinormal distribution has an absolute maximum, it may have multiple "peaks" (i.e. relative maxima). In general, the tails of each of the associated marginal PDFs are "fat" in the sense that the marginal PDF decreases algebraically rather than exponentially for large values of 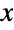 . (This behavior can be made quantitatively precise by analyzing the SurvivalFunction of these marginal distributions.)
. (This behavior can be made quantitatively precise by analyzing the SurvivalFunction of these marginal distributions.) - The study of multivariate positive distributions (i.e. those in which each of the coordinates of the variate vector are positive) became popular in the 1970s when Johnson and Kotz investigated the multivariate versions of the GammaDistribution, BetaDistribution, ParetoDistribution, and FRatioDistribution in applications such as economics, psychology, and reliability. In 2001, the log-multinormal distribution was introduced as an appealing alternative when modeling multi-variable, coordinate-wise positive phenomena due to the relatively simple forms of its PDF and its CDF (cumulative distribution function).
- RandomVariate can be used to give one or more machine- or arbitrary-precision (the latter via the WorkingPrecision option) pseudorandom variates from a log-multinormal distribution. Distributed[x,LogMultinormalDistribution[μ,Σ]] , written more concisely as xLogMultinormalDistribution[μ,Σ], can be used to assert that a random variable x is distributed according to a log-multinormal distribution. Such an assertion can then be used in functions such as Probability, NProbability, Expectation, and NExpectation.
- The probability density and cumulative distribution functions for log-multinormal distributions may be given using PDF[LogMultinormalDistribution[μ,Σ],x] and CDF[LogMultinormalDistribution[μ,Σ],x]. The mean, median, variance, raw moments, and central moments may be computed using Mean, Median, Variance, Moment, and CentralMoment, respectively.
- DistributionFitTest can be used to test if a given dataset is consistent with a log-multinormal distribution, EstimatedDistribution to estimate a log-multinormal parametric distribution from given data, and FindDistributionParameters to fit data to a log-multinormal distribution. ProbabilityPlot can be used to generate a plot of the CDF of given data against the CDF of a symbolic log-multinormal distribution and QuantilePlot to generate a plot of the quantiles of given data against the quantiles of a symbolic log-multinormal distribution.
- TransformedDistribution can be used to represent a transformed log-multinormal distribution, CensoredDistribution to represent the distribution of values censored between upper and lower values, and TruncatedDistribution to represent the distribution of values truncated between upper and lower values. CopulaDistribution can be used to build higher-dimensional distributions that contain a log-multinormal distribution, and ProductDistribution can be used to compute a joint distribution with independent component distributions involving log-multinormal distributions.
- LogMultinormalDistribution is related to a number of other distributions. LogMultinormalDistribution is connected to NormalDistribution, BinormalDistribution, LogNormalDistribution, and MultinormalDistribution as discussed above, and its logarithmic behavior is qualitatively similar to that of LogLogisticDistribution, LogNormalDistribution, and LogGammaDistribution. The one-dimensional marginals PDF of LogMultinormalDistribution are LogNormalDistribution, while each of the multivariate marginals is again an instance of LogMultinormalDistribution. LogMultinormalDistribution can be realized as a transformation (TransformedDistribution) of each of MultinormalDistribution, BinormalDistribution, and LogNormalDistribution, while also being obtained as a product distribution (ProductDistribution) of LogNormalDistribution when Σ is a diagonal matrix. Because of its relation to the univariate distributions NormalDistribution and LogNormalDistribution, it is also related to DavisDistribution, LogLogisticDistribution, ExponentialDistribution, WeibullDistribution, GompertzMakehamDistribution, ExtremeValueDistribution, and GammaDistribution.
Examples
open allclose allBasic Examples (4)
Scope (6)
Generate a sample of pseudorandom vectors from a log-multinormal distribution:
Visualize the sample using a histogram:
Distribution parameters estimation:
Estimate the distribution parameters from sample data:
Univariate marginals follow LogNormalDistribution:
Multivariate marginals follow a log-multinormal distribution:
Properties & Relations (7)
Relationships to other distributions:
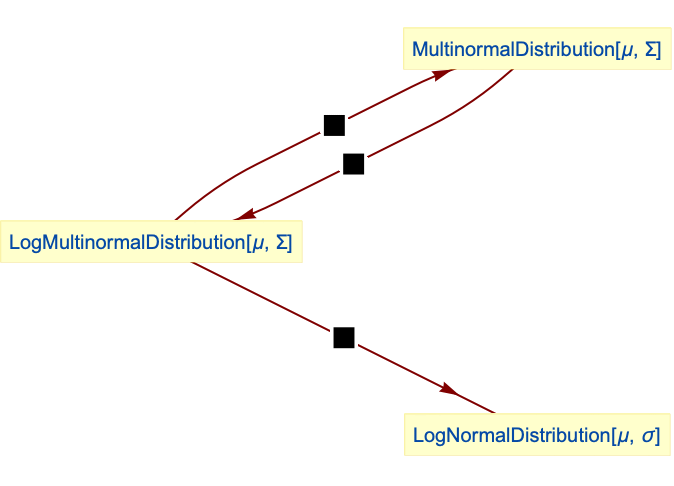
LogMultinormalDistribution is a transformation of MultinormalDistribution:
LogMultinormalDistribution is a transformation of BinormalDistribution:
One-dimensional marginal is LogNormalDistribution:
Special case with diagonal matrix is ProductDistribution of LogNormalDistribution:
LogMultinormalDistribution is related to LogNormalDistribution:
LogMultinormalDistribution is a slice distribution for GeometricBrownianMotionProcess:
Text
Wolfram Research (2012), LogMultinormalDistribution, Wolfram Language function, https://reference.wolfram.com/language/ref/LogMultinormalDistribution.html.
CMS
Wolfram Language. 2012. "LogMultinormalDistribution." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/LogMultinormalDistribution.html.
APA
Wolfram Language. (2012). LogMultinormalDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/LogMultinormalDistribution.html