BeckmannDistribution
BeckmannDistribution[μ1,μ2,σ1,σ2]
represents the Beckmann distribution with means μ1 and μ2 and standard deviations σ1 and σ2.
BeckmannDistribution[μ1,μ2,σ1,σ2,ρ]
represents the Beckmann distribution with means μ1 and μ2, standard deviations σ1 and σ2, and correlation ρ.
Details
- If {x,y} follows BinormalDistribution[{μ1,μ2},{σ1,σ2}, ρ],
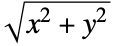 follows BeckmannDistribution[{μ1,μ2},{σ1,σ2}, ρ].
follows BeckmannDistribution[{μ1,μ2},{σ1,σ2}, ρ]. - BeckmannDistribution allows μi to be any real numbers, σi any positive real numbers, and ρ any number between -1 and 1.
- BeckmannDistribution allows μi and σi to be quantities with the same unit dimensions, and ρ to be a dimensionless quantity. »
- BeckmannDistribution can be used with such functions as Mean, CDF, and RandomVariate.
Background & Context
- BeckmannDistribution[μ1,μ2,σ1,σ2,ρ] represents a continuous probability distribution defined over the interval
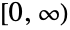 and parametrized by the numbers μ1, μ2, σ1, σ2, and ρ. Here, μ1 and μ2 are arbitrary real numbers, σ1 and σ2 are positive real numbers, and ρ is a real number satisfying
and parametrized by the numbers μ1, μ2, σ1, σ2, and ρ. Here, μ1 and μ2 are arbitrary real numbers, σ1 and σ2 are positive real numbers, and ρ is a real number satisfying 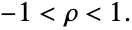 The overall shape of the probability density function (PDF) of a Beckmann distribution depends on its arguments. For example, while the PDF of a Beckmann distribution is always unimodal, the shape of the PDF around its peak (e.g. its concavity) depends on the arguments. In general, higher values of σi tend to increase the "steepness" of the PDF near the peak, while lower values "spread out" the distribution in a way that makes the peak itself less discernible. Varying the parameter μi can change both the height and the horizontal position of the PDF, while varying ρ can affect its height and its overall concavity. The four-argument form BeckmannDistribution[μ1,μ2,σ1,σ2] is equivalent to BeckmannDistribution[μ1,μ2,σ1,σ2,0] and is sometimes referred to as the uncorrelated Beckmann distribution.
The overall shape of the probability density function (PDF) of a Beckmann distribution depends on its arguments. For example, while the PDF of a Beckmann distribution is always unimodal, the shape of the PDF around its peak (e.g. its concavity) depends on the arguments. In general, higher values of σi tend to increase the "steepness" of the PDF near the peak, while lower values "spread out" the distribution in a way that makes the peak itself less discernible. Varying the parameter μi can change both the height and the horizontal position of the PDF, while varying ρ can affect its height and its overall concavity. The four-argument form BeckmannDistribution[μ1,μ2,σ1,σ2] is equivalent to BeckmannDistribution[μ1,μ2,σ1,σ2,0] and is sometimes referred to as the uncorrelated Beckmann distribution. - BeckmannDistribution[μ1,μ2,σ1,σ2,ρ] is defined as the distribution according to which
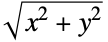 is distributed when each element of the pair
is distributed when each element of the pair  is distributed according to BinormalDistribution[{μ1,μ2},{σ1,σ2}, ρ]. As a result, the norm of a two-dimensional vector with normally distributed and correlated components follows a Beckmann distribution. The Beckmann distribution plays a fundamental role in scientific visualization, particularly in determining details concerning shading and specular highlighting in three-dimensional computer graphics, and is used to model fading amplitude in the theory of fading channels.
is distributed according to BinormalDistribution[{μ1,μ2},{σ1,σ2}, ρ]. As a result, the norm of a two-dimensional vector with normally distributed and correlated components follows a Beckmann distribution. The Beckmann distribution plays a fundamental role in scientific visualization, particularly in determining details concerning shading and specular highlighting in three-dimensional computer graphics, and is used to model fading amplitude in the theory of fading channels. - RandomVariate can be used to give one or more machine- or arbitrary-precision (the latter via the WorkingPrecision option) pseudorandom variates from a Beckmann distribution. Distributed[x,BeckmannDistribution[μ1,μ2,σ1,σ2,ρ]], written more concisely as xBeckmannDistribution[μ1,μ2,σ1,σ2,ρ], can be used to assert that a random variable x is distributed according to a Beckmann distribution. Such an assertion can then be used in functions such as Probability, NProbability, Expectation, and NExpectation.
- The probability density and cumulative distribution functions may be given using PDF[BeckmannDistribution[μ1,μ2,σ1,σ2,ρ],x] and CDF[BeckmannDistribution[μ1,μ2,σ1,σ2,ρ],x]. The mean, median, variance, raw moments, and central moments may be computed using Mean, Median, Variance, Moment, and CentralMoment, respectively.
- DistributionFitTest can be used to test if a given dataset is consistent with a Beckmann distribution, EstimatedDistribution to estimate a Beckmann parametric distribution from given data, and FindDistributionParameters to fit data to a Beckmann distribution. ProbabilityPlot can be used to generate a plot of the CDF of given data against the CDF of a symbolic Beckmann distribution, and QuantilePlot to generate a plot of the quantiles of given data against the quantiles of a symbolic Beckmann distribution.
- TransformedDistribution can be used to represent a transformed Beckmann distribution, CensoredDistribution to represent the distribution of values censored between upper and lower values, and TruncatedDistribution to represent the distribution of values truncated between upper and lower values. CopulaDistribution can be used to build higher-dimensional distributions that contain a Beckmann distribution, and ProductDistribution can be used to compute a joint distribution with independent component distributions involving Beckmann distributions.
- BeckmannDistribution is closely related to a number of other distributions. For example, BeckmannDistribution can be realized as a transformation of both NormalDistribution and BinormalDistribution, and can itself be transformed to realize NoncentralChiSquareDistribution. In addition, HoytDistribution and RiceDistribution are also both special cases of BeckmannDistribution.
Examples
open allclose allScope (5)
Generate a sample of pseudorandom numbers from a Beckmann distribution:
Compare the histogram to the PDF:
Distribution parameters estimation:
Estimate the distribution parameters from sample data:
Compare a density histogram of the sample with the PDF of the estimated distribution:
Consistent use of Quantity in parameters yields QuantityDistribution:
Applications (2)
The length of a 2D vector with normally distributed and correlated components follows a Beckmann distribution:
Find the probability that a vector is longer than 3.5 cm:
Find the average length of a vector:
Simulate possible lengths for a sample of 30 vectors:
In the theory of fading channels, BeckmannDistribution is used to model fading amplitude. Find the distribution of instantaneous signal-to-noise ratio where ![]() ,
, ![]() is the energy per symbol, and
is the energy per symbol, and ![]() is the spectral density of white noise:
is the spectral density of white noise:
Properties & Relations (8)
A Beckmann distribution is closed under scaling by a positive number:
Relationships to other distributions:
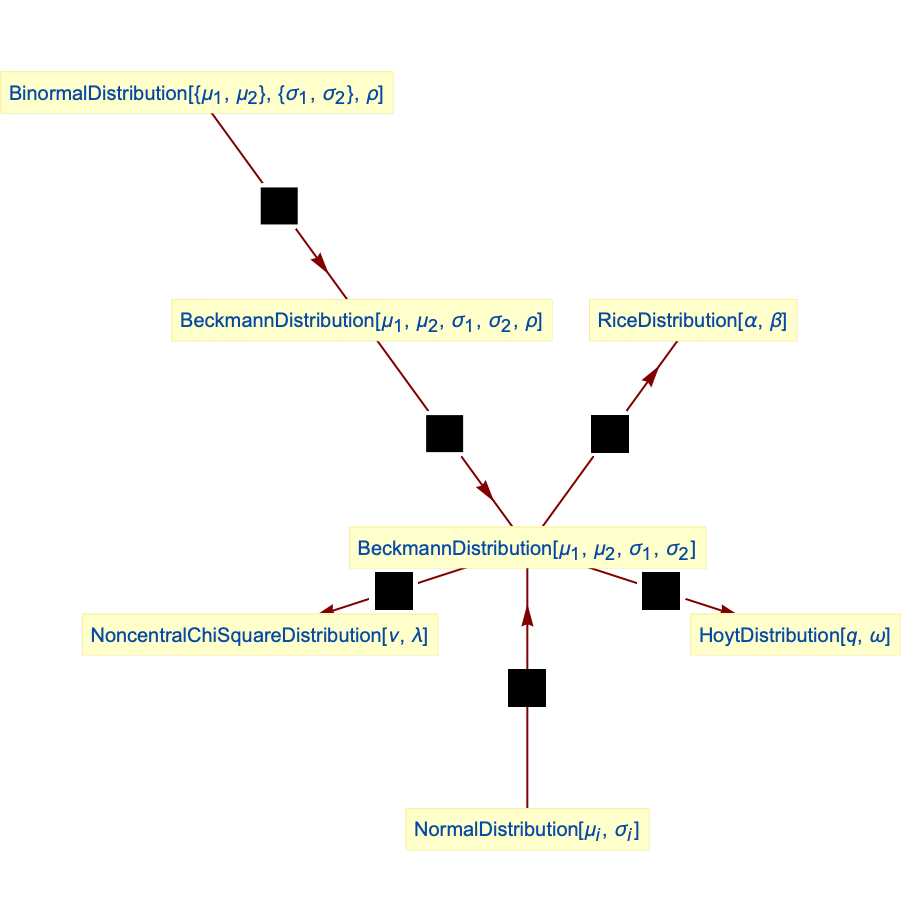
For ![]() , a Beckmann distribution simplifies to an uncorrelated case:
, a Beckmann distribution simplifies to an uncorrelated case:
Beckmann distribution is related to NoncentralChiSquareDistribution:
The norm of the vector of two components from NormalDistribution has a Beckmann distribution:
Beckmann distribution is related to BinormalDistribution:
HoytDistribution can be obtained from a Beckmann distribution:
RiceDistribution is a special case of a Beckmann distribution:
Text
Wolfram Research (2010), BeckmannDistribution, Wolfram Language function, https://reference.wolfram.com/language/ref/BeckmannDistribution.html (updated 2016).
CMS
Wolfram Language. 2010. "BeckmannDistribution." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/BeckmannDistribution.html.
APA
Wolfram Language. (2010). BeckmannDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/BeckmannDistribution.html