



EllipticE
Details

- Mathematical function, suitable for both symbolic and numerical manipulation.
- For
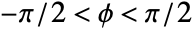 and
and 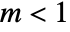 ,
, ![TemplateBox[{phi, m}, EllipticE2]=int_0^phi(1-m sin^2(theta))^(1/2)dtheta TemplateBox[{phi, m}, EllipticE2]=int_0^phi(1-m sin^2(theta))^(1/2)dtheta](Files/EllipticE.en/5.png) .
. ![TemplateBox[{m}, EllipticE]=TemplateBox[{{pi, /, 2}, m}, EllipticE2] TemplateBox[{m}, EllipticE]=TemplateBox[{{pi, /, 2}, m}, EllipticE2]](Files/EllipticE.en/6.png) .
. - EllipticE[m] has a branch cut discontinuity in the complex m plane running from
 to
to 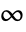 .
. - EllipticE[ϕ,m] has branch cut discontinuities at
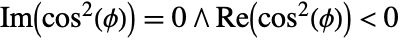 and at
and at 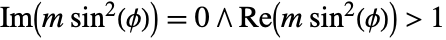 .
. - For certain special arguments, EllipticE automatically evaluates to exact values.
- EllipticE can be evaluated to arbitrary numerical precision.
- EllipticE automatically threads over lists.
- EllipticE can be used with Interval and CenteredInterval objects. »
Examples
open all close allBasic Examples (5)
Plot over a subset of the reals:
Plot over a subset of the complexes:
Series expansion at the origin:
Series expansion at Infinity:
Scope (41)
Numerical Evaluation (5)
Evaluate numerically for complex arguments:
The precision of the output tracks the precision of the input:
Evaluate EllipticE efficiently at high precision:
Compute worst-case guaranteed intervals using Interval and CenteredInterval objects:
Or compute average-case statistical intervals using Around:
Compute the elementwise values of an array:
Or compute the matrix EllipticE function using MatrixFunction:
Specific Values (4)
Visualization (3)
Function Properties (10)
![]() is defined for all real values less than or equal to 1:
is defined for all real values less than or equal to 1:
![]() takes all real values greater than or equal to 1:
takes all real values greater than or equal to 1:
EllipticE is an odd function with respect to its first parameter:
EllipticE is not an analytic function:
Has both singularities and discontinuities for ![]() :
:
EllipticE is not a meromorphic function:
![]() is nonincreasing on its domain:
is nonincreasing on its domain:
Differentiation (4)
Integration (3)
Indefinite integral of EllipticE:
Definite integral of an odd function over an interval centered at the origin is 0:
Series Expansions (4)
Integral Transforms (2)
Function Representations (6)
The definition of the elliptic integral of the second kind:
Complete elliptic integral is a partial case of the elliptic integral of the second kind:
Relation to other elliptic integrals:
Represent in terms of MeijerG using MeijerGReduce:
EllipticE can be represented as a DifferentialRoot:
TraditionalForm formatting:
Applications (10)
Plot an incomplete elliptic integral over the complex plane:
Perimeter length of an ellipse:
Use ArcLength to obtain the perimeter:
Series expansion for almost equal axes lengths:
Compare with an approximation by Ramanujan:
Arc length of a hyperbola as a function of the angle of a point on the hyperbola:
Plot the arc length as a function of the angle:
Vector potential of a ring current in cylindrical coordinates:
The vertical and radial components of the magnetic field:
Plot magnitude of the magnetic field:
Inductance of a solenoid of radius r and length a with fixed numbers of turns per unit length:
Inductance per unit length of the infinite solenoid:
Calculate the surface area of a triaxial ellipsoid:
The area of an ellipsoid with half axes 3, 2, 1:
Calculate the area by integrating the differential surface elements:
Parametrization of a Mylar balloon (two flat sheets of plastic sewn together at their circumference and then inflated):
Calculate the ratio of the main curvatures:
Express the radius of the original sheets in terms of the radius of the inflated balloon:
Parametrize an ellipse using EllipticE :
Plot using elliptic parametrization and circular parametrization:
Define the Halphen constant using elliptic integrals [MathWorld]:
Properties & Relations (6)
EllipticE[ϕ,m] is real‐valued for real argument subject to the following conditions:
For real arguments, if ![]() , then
, then ![]() for
for ![]() :
:
Expand special cases under argument restrictions:
Numerically find a root of a transcendental equation:
EllipticE is automatically returned as a special case for some special functions:
Tech Notes
Related Guides
Related Links
History
Introduced in 1988 (1.0) | Updated in 1996 (3.0) ▪ 2020 (12.2) ▪ 2021 (13.0) ▪ 2022 (13.1)
Text
Wolfram Research (1988), EllipticE, Wolfram Language function, https://reference.wolfram.com/language/ref/EllipticE.html (updated 2022).
CMS
Wolfram Language. 1988. "EllipticE." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2022. https://reference.wolfram.com/language/ref/EllipticE.html.
APA
Wolfram Language. (1988). EllipticE. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/EllipticE.html
BibTeX
@misc{reference.wolfram_2025_elliptice, author="Wolfram Research", title="{EllipticE}", year="2022", howpublished="\url{https://reference.wolfram.com/language/ref/EllipticE.html}", note=[Accessed: 23-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_elliptice, organization={Wolfram Research}, title={EllipticE}, year={2022}, url={https://reference.wolfram.com/language/ref/EllipticE.html}, note=[Accessed: 23-February-2026]}