ImageDistance

ImageDistance[image1,image2]

returns a distance measure between image1 and image2.

ImageDistance[image1,image2,pos]

places the center of image2 at position pos in image1.

ImageDistance[image1,image2,pos1,pos2]

places the point pos2 of image2 at position pos1 in image1.

Details and Options

  • ImageDistance[image1,image2] centers image2 in image1 and returns the distance between the overlapping regions in the two images.
  • ImageDistance works with arbitrary 2D and 3D images.
  • Images should either have the same number of channels or one should be a single-channel image. If either of image1 or image2 is a single-channel image, the channel is replicated to match the number of channels in the other image.
  • Position specification pos can be of the form:
  • {x,y} or {x,y,z}absolute pixel position
    Scaled[{sx,…}]scaled position from 0 to 1 across the object
    Centercenter alignment
    Left,Right 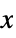axis in both 2D and 3D
    Bottom,Top 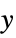axis in 2D, 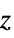axis in 3D
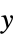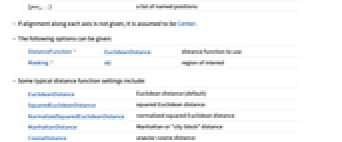
    Front,Back axis in 3D
    {posx,…}a list of named positions
  • If alignment along each axis is not given, it is assumed to be Center.
  • The following options can be given:
  • DistanceFunction EuclideanDistancedistance function to use
    Masking Allregion of interest
  • Some typical distance function settings include:
  • EuclideanDistanceEuclidean distance (default)
    SquaredEuclideanDistancesquared Euclidean distance
    NormalizedSquaredEuclideanDistancenormalized squared Euclidean distance
    ManhattanDistanceManhattan or "city block" distance
    CosineDistanceangular cosine distance
    CorrelationDistancecorrelation coefficient distance
    ffunction f that is given the overlapping regions of the two images as arguments
  • The following special distance functions are also supported:
  • "MeanEuclideanDistance"mean Euclidean distance
    "MeanSquaredEuclideanDistance"mean squared Euclidean distance
    "RootMeanSquare"mean squared root distance
    {"MeanReciprocalSquaredEuclideanDistance",λ}one minus the mean of the robust distances 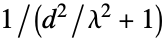, where 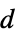is the Euclidean distance of corresponding pixels (default )
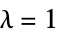    {"MutualInformationVariation",n}joint entropy minus mutual information using n-bin histogram (default )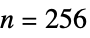
    {"NormalizedMutualInformationVariation",n}the mutual information variation divided by the joint entropy using n-bin histogram (default )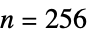
    {"DifferenceNormalizedEntropy",n}entropy of the difference image using n-bin histogram (default )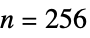
    "MeanPatternIntensity"mean local pattern intensity difference
    "GradientCorrelation"mean of the correlation distances between the spatial derivatives
    "MeanReciprocalGradientDistance"one minus the mean of the distances 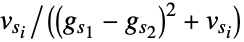, with values 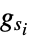and variances 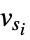of the spatial derivatives along dimension s of imagei
    {"EarthMoverDistance",n}earth mover distance using n-bin histogram
  • Using Masking->roi, a region of interest in image1 is specified. With Masking->{roi1,roi2}, the intersection of roi1 and roi2 on the overlapped images is used.
  • Predefined ImageDistance metrics are symmetric and non-negative. However, some distances may not satisfy the triangle inequality. The distance between two images can be 0 with some methods, even if they are not identical. User-defined functions might break these properties.
  • If there are no overlapping regions or the measure cannot be determined, Indeterminate is returned. »

Examples

open allclose all

Basic Examples  (2)

Euclidean distance between two images:

Euclidean distance between 3D images:

Scope  (2)

By default, images are center aligned:

Align the top-left corner of the first image with the center of the second image:

Align the center top of the first image and right center of the second image:

Specify positions using the standard coordinate system:

Specify positions using scaled coordinates:

Specify the alignment position for 3D images:

Options  (8)

DistanceFunction  (5)

Use a custom distance function:

Use a custom distance function with masks:

Earth mover distance:

Use histograms with four bins per channel:

Compare different distance measures:

Compute the root mean square distance of approximate perceptual distances between pixels:

Masking  (3)

Use a mask to specify the region of interest in the first image:

Use a mask to specify the region of interest in the second image:

Use masks for both images:

Applications  (2)

Construct a similarity graph of a set of images based on the earth mover distance:

Compute a matrix of distances for all image pairs:

Threshold the distances to construct an adjacency matrix and visualize using a graph:

Register two images related by a translation and a rotation:

Properties & Relations  (8)

The distance between an image and itself is always zero:

The distance between two different images may be 0:

The distance between two images is symmetric:

The distance may not be symmetric with masks:

When the images have no overlap, the distance is indeterminate:

The distance between an image and its rotations:

Normalized mutual information variation of an MRI and a translated PET image:

Correcting for overall change in brightness is a typical preprocessing with some distances:

Without correction, it is less apparent that the two images are aligned:

Some distance measures are effectively invariant to specific transformations.

Spatial reflection:

Color negation:

Pointwise addition:

Pointwise multiplication by a positive number:

Pointwise affine transformation with positive slope coefficient:

For a rectangular mask, image distance is equal to the distance of the trimmed images:

Wolfram Research (2012), ImageDistance, Wolfram Language function, https://reference.wolfram.com/language/ref/ImageDistance.html (updated 2016).

Text

Wolfram Research (2012), ImageDistance, Wolfram Language function, https://reference.wolfram.com/language/ref/ImageDistance.html (updated 2016).

CMS

Wolfram Language. 2012. "ImageDistance." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/ImageDistance.html.

APA

Wolfram Language. (2012). ImageDistance. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ImageDistance.html

BibTeX

@misc{reference.wolfram_2025_imagedistance, author="Wolfram Research", title="{ImageDistance}", year="2016", howpublished="\url{https://reference.wolfram.com/language/ref/ImageDistance.html}", note=[Accessed: 18-February-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_imagedistance, organization={Wolfram Research}, title={ImageDistance}, year={2016}, url={https://reference.wolfram.com/language/ref/ImageDistance.html}, note=[Accessed: 18-February-2025 ]}