ListCorrelate

ListCorrelate[ker,list]

forms the correlation of the kernel ker with list.

ListCorrelate[ker,list,k]

forms the cyclic correlation in which the k^(th) element of ker is aligned with each element in list.

ListCorrelate[ker,list,{kL,kR}]

forms the cyclic correlation whose first element contains list[[1]]ker[[kL]] and whose last element contains list[[-1]]ker[[kR]].

ListCorrelate[ker,list,klist,p]

forms the correlation in which list is padded at each end with repetitions of the element p.

ListCorrelate[ker,list,klist,{p1,p2,…}]

forms the correlation in which list is padded at each end with cyclic repetitions of the pi.

ListCorrelate[ker,list,klist,padding,g,h]

forms a generalized correlation in which g is used in place of Times and h in place of Plus.

ListCorrelate[ker,list,klist,padding,g,h,lev]

forms a correlation using elements at level lev in ker and list.

Details

  • With kernel Kr and list as, ListCorrelate[ker,list] computes 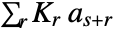, where the limits of the sum are such that the kernel never overhangs either end of the list.
  • For a one‐dimensional list ListCorrelate[ker,list] is equivalent to ListConvolve[Reverse[ker],list].
  • For higher-dimensional lists, ker must be reversed at every level.
  • Settings for kL and kR are negated in ListConvolve relative to ListCorrelate.
  • Common settings for {kL,kR} in ListCorrelate are:
  • {1,-1}no overhangs (default)
    {1,1}maximal overhang at the right‐hand end
    {-1,-1}maximal overhang at the left‐hand end
    {-1,1}maximal overhangs at both beginning and end

Examples

open allclose all

Basic Examples  (4)

Correlate a kernel {x,y} with a list of data:

Make a cyclic correlation the same length as the original data:

Align element 2 in the kernel with successive elements in the data:

Pad with zzz instead of using the data cyclically:

Two-dimensional correlation:

Scope  (5)

Use exact arithmetic to compute the correlation:

Use machine arithmetic:

Use 24-digit precision arithmetic:

Correlation of complex data:

Two-dimensional correlation:

Cyclic two-dimensional correlation:

Two-dimensional correlation with maximal overhangs and zero padding:

Generalizations & Extensions  (4)

Use functions f and g in place of Plus and Times:

Use functions f and g in place of Plus and Times with maximal overhangs and zero padding:

Use functions f and g in place of Plus and Times with maximal overhangs and empty padding:

ListCorrelate works with TimeSeries:

Applications  (6)

Smooth data with a weighted running average:

Normalized Gaussian profile for averaging weights:

Gaussian smoothing of an image:

Gaussian kernel with a 5×5 pixel stencil:

Smooth the image:

Edge detection in an image:

Correlate with a Laplacian filter kernel:

Use a Laplacian of a Gaussian filter kernel:

Generate Pascal's triangle:

Additive cellular automata:

Apply a finite difference formula to a uniformly sampled function:

Show the error for different numbers of grid points:

Show the error for different numbers of grid points for a second derivative approximation:

Properties & Relations  (3)

ListCorrelate is equivalent to ListConvolve with the kernel reversed:

Generate two random vectors:

A function for constructing a circulant matrix from a vector:

Cyclic correlation is equivalent to multiplication with a circulant matrix:

Cyclic correlation is also equivalent to multiplication in the discrete Fourier transform domain:

Generate two random vectors:

A function for constructing an upper triangular Toeplitz matrix from a vector:

Cyclic correlation with zero-padding is equivalent to multiplication with an upper triangular Toeplitz matrix:

Wolfram Research (1999), ListCorrelate, Wolfram Language function, https://reference.wolfram.com/language/ref/ListCorrelate.html.

Text

Wolfram Research (1999), ListCorrelate, Wolfram Language function, https://reference.wolfram.com/language/ref/ListCorrelate.html.

CMS

Wolfram Language. 1999. "ListCorrelate." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/ListCorrelate.html.

APA

Wolfram Language. (1999). ListCorrelate. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ListCorrelate.html

BibTeX

@misc{reference.wolfram_2024_listcorrelate, author="Wolfram Research", title="{ListCorrelate}", year="1999", howpublished="\url{https://reference.wolfram.com/language/ref/ListCorrelate.html}", note=[Accessed: 14-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_listcorrelate, organization={Wolfram Research}, title={ListCorrelate}, year={1999}, url={https://reference.wolfram.com/language/ref/ListCorrelate.html}, note=[Accessed: 14-November-2024 ]}