Wolfram ResearchProductsPurchasingServices & ResourcesAbout UsOur Sites
DOCUMENTATION CENTER SEARCH
Mathematica > Operations on Vectors >
Built-in Mathematica SymbolTutorials »|See Also »|More About »

Orthogonalize

Orthogonalize[{v1, v2, ...}]
gives an orthonormal basis found by orthogonalizing the vectors vi.
Orthogonalize[{e1, e2, ...}, f]
gives a basis for the ei orthonormal with respect to the inner product function f.
  • Orthogonalize[{v1, v2, ...}] uses the ordinary scalar product 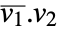as an inner product.
  • The output from Orthogonalize always contains the same number of vectors as the input. If some of the input vectors are not linearly independent, the output will contain zero vectors.
  • All nonzero vectors in the output are normalized to unit length.
  • The inner product function f is applied to pairs of linear combinations of the ei.
  • The ei can be any expressions for which f always yields real results.
  • Orthogonalize[{v1, v2, ...}, Dot] effectively assumes that all elements of the vi are real.
  • Other bases can be obtained by giving alternative settings for the Method option. Possible settings include: "GramSchmidt", "ModifiedGramSchmidt", "Reorthogonalization" and "Householder".
New in 6
© 2008 Wolfram Research, Inc. japanese.gif
Ask a question about this page  |  Suggest an improvement  |  Leave a message for the team