ShortTimeFourier

ShortTimeFourier[data]

returns the short-time Fourier transform (STFT) of data as a ShortTimeFourierData object.

ShortTimeFourier[data,n]

uses partitions of length n.

ShortTimeFourier[data,n,d]

uses partitions with offset d.

ShortTimeFourier[data,n,d,wfun]

applies a smoothing window wfun to each partition.

ShortTimeFourier[data,n,d,wfun,m]

pads partitions with zeros to length m prior to the computation of the transform.

Details and Options

  • The short-time Fourier transform (STFT) is a time-frequency representation of a signal and is typically used for transforming, filtering and analyzing the signal in both time and frequency.
  • ShortTimeFourier[data] computes the discrete Fourier transform (DFT) of partitions of data and returns a ShortTimeFourierData object.
  • Use Spectrogram on data or on the resulting ShortTimeFourierData object to plot the spectrogram.
  • ShortTimeFourier[data] uses partitions of length n=2^Round[InterpretationBox[{log, _, DocumentationBuild`Utils`Private`Parenth[2]}, Log2, AutoDelete -> True](sqrt(m))+1] and offset d=Round[n/3], where 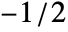is Length[data].
  • The partition length n and offset d can be expressed as integer numbers (interpreted as number of samples) or as time or sample quantities.
  • If necessary, fixed padding is used on the right to make all the partitions the same size.
  • In ShortTimeFourier[data,n,d,wfun], the smoothing window wfun can be specified using a window function that will be sampled between 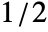and 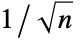or a list of length n. The default window is DirichletWindow, which effectively does no smoothing.
  • The data can be any of the following:
  • listarbitrary rank numerical array
    audioan Audio or Sound object
    videoa Video object
  • For multichannel audio objects, the spectrogram is computed over the sum of all channels.
  • ShortTimeFourier accepts the FourierParameters option. The default setting is FourierParameters->{1,-1}.

Examples

open allclose all

Basic Examples  (2)

Short-time Fourier transform of a sine wave:

Short-time Fourier transform of an audio signal:

Plot the result:

Scope  (7)

Data  (3)

Short-time Fourier transform of an audio recording:

Short-time Fourier transform of an array:

Short-time Fourier transform of the audio track of a video:

Parameters  (4)

By default, an automatic partition size is used:

Specify the number of samples in each partition:

Specify the partition size using a time Quantity:

By default, an automatic partition offset is used:

Specify the offset using the number of samples:

Specify the offset using a time Quantity:

Use Scaled to specify offset relative to the partition size:

By default, no smoothing is applied to partitions:

Using None or DirichletWindow is equivalent to no smoothing:

Use a HannWindow as smoothing window function:

Use a precomputed list as smoothing window function:

By default, partitions are not padded:

Pad each partition to be 20 samples long:

Specify padding using a time Quantity:

Options  (3)

FourierParameters  (3)

No normalization:

Normalization by :

Normalization by :

Applications  (6)

Compute the full short-time Fourier transform of a signal:

Plot of the magnitude of the ShortTimeFourier data:

Apply a smoothing window function:

Magnitude spectrum of a single partition:

Compute the full short-time Fourier transform of a signal:

Compute the magnitude spectrogram:

Compute the power spectrogram:

Compute the power spectrogram in decibels:

Compute the forward and inverse short-time Fourier transform of a signal:

Compute the short-time Fourier transform:

Approximate the inverse using InverseShortTimeFourier:

Denoise a chirp signal:

Compute the full short-time Fourier transform of the signal:

Define a nonlinear function to squash low-amplitude components:

Apply the function to the short-time Fourier transform data:

Invert the short-time Fourier transform using InverseShortTimeFourier:

Change the speed of an audio recording using different STFT partition offsets:

Change the "PartitionOffset" property:

Compute the inverse short-time Fourier transform to speed up the recording:

Slow down an audio signal by resampling the short-time Fourier transform:

Resample the data:

Compute the inverse short-time Fourier transform to get a slowed-down version of the original:

Properties & Relations  (2)

Short-time Fourier transform data is the same as the values computed by SpectrogramArray:

Spectrogram of the ShortTimeFourier is equivalent to Spectrogram of the original signal:

Notice that the default partitioning parameters are different:

Wolfram Research (2019), ShortTimeFourier, Wolfram Language function, https://reference.wolfram.com/language/ref/ShortTimeFourier.html (updated 2024).

Text

Wolfram Research (2019), ShortTimeFourier, Wolfram Language function, https://reference.wolfram.com/language/ref/ShortTimeFourier.html (updated 2024).

CMS

Wolfram Language. 2019. "ShortTimeFourier." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2024. https://reference.wolfram.com/language/ref/ShortTimeFourier.html.

APA

Wolfram Language. (2019). ShortTimeFourier. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ShortTimeFourier.html

BibTeX

@misc{reference.wolfram_2024_shorttimefourier, author="Wolfram Research", title="{ShortTimeFourier}", year="2024", howpublished="\url{https://reference.wolfram.com/language/ref/ShortTimeFourier.html}", note=[Accessed: 21-December-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_shorttimefourier, organization={Wolfram Research}, title={ShortTimeFourier}, year={2024}, url={https://reference.wolfram.com/language/ref/ShortTimeFourier.html}, note=[Accessed: 21-December-2024 ]}