Numbers
| Integer | arbitrary‐length exact integer |
| Rational | integer/integer in lowest terms |
| Real |
approximate real number, with any specified precision
|
| Complex | complex number of the form number+number I |
| 123 | an exact integer |
| 123. | an approximate real number |
| 123.0000000000000 | an approximate real number with a certain precision |
| 123.+0.I | a complex number with approximate real number components |
You can distinguish different types of numbers in the Wolfram System by looking at their heads. (Although numbers in the Wolfram System have heads like other expressions, they do not have explicit elements which you can extract.)
The presence of an explicit decimal point makes the Wolfram System treat 123. as an approximate real number, with head Real:
| NumberQ[x] | test whether x is any kind of number |
| IntegerQ[x] | test whether x is an integer |
| EvenQ[x] | test whether x is even |
| OddQ[x] | test whether x is odd |
| PrimeQ[x] | test whether x is a prime integer |
| Head[x]===type | test the type of a number |
NumberQ[x] tests for any kind of number:
If you use complex numbers extensively, there is one subtlety you should be aware of. When you enter a number like 123., the Wolfram System treats it as an approximate real number, but assumes that its imaginary part is exactly zero. Sometimes you may want to enter approximate complex numbers with imaginary parts that are zero, but only to a certain precision.
When the imaginary part is the exact integer 0, the Wolfram System simplifies complex numbers to real ones:
Here the imaginary part is only zero to a certain precision, so the Wolfram System retains the complex number form:
The distinction between complex numbers whose imaginary parts are exactly zero, or are only zero to a certain precision, may seem like a pedantic one. However, for example, when the interpretation of powers and roots of complex numbers is discussed in "Functions That Do Not Have Unique Values", the distinction becomes significant.
One way to find out the type of a number in Wolfram System is just to pick out its head using Head[expr]. For many purposes, however, it is better to use functions like IntegerQ that explicitly test for particular types. Functions like this are set up to return True if their argument is manifestly of the required type, and to return False otherwise. As a result, IntegerQ[x] will give False unless x has an explicit integer value.
You can enter complex numbers in the Wolfram Language just by including the constant I, equal to  . Make sure that you type a capital I.
. Make sure that you type a capital I.
If you are using notebooks, you can also enter I as  by typing EsciiEsc (see "Mathematical Notation in Notebooks: Numerical Calculations"). The form
by typing EsciiEsc (see "Mathematical Notation in Notebooks: Numerical Calculations"). The form  is normally what is used in output. Note that an ordinary i means a variable named
is normally what is used in output. Note that an ordinary i means a variable named 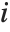 , not
, not  .
.
| x+I y | the complex number |
| Re[z] | real part |
| Im[z] | imaginary part |
| Conjugate[z] | complex conjugate |
| Abs[z] | absolute value |
| Arg[z] | the argument |
| NumberQ[expr] | test whether expr is explicitly a number |
| NumericQ[expr] | test whether expr has a numerical value |
This finds the explicit numerical value of Pi+3:
The Wolfram Language knows that constants such as Pi are numeric quantities. It also knows that standard mathematical functions such as Log and Sin have numerical values when their arguments are numerical.
In general, the Wolfram Language assumes that any function which has the attribute NumericFunction will yield numerical values when its arguments are numerical. All standard mathematical functions in the Wolfram Language already have this attribute. But when you define your own functions, you can explicitly set the attribute to tell the Wolfram Language to assume that these functions will have numerical values when their arguments are numerical.
| IntegerDigits[n] | a list of the decimal digits in the integer n |
| IntegerDigits[n,b] | the digits of n in base b |
| IntegerDigits[n,b,len] | the list of digits padded on the left with zeros to give total length len |
| IntegerLength[n] | the number of decimal digits in n |
| IntegerLength[n,b] | the number of base b digits in n |
| IntegerExponent[n,b] | the number of zeros at the end of n in base b |
| RealDigits[x] | a list of the decimal digits in the approximate real number x, together with the number of digits to the left of the decimal point |
| RealDigits[x,b] | the digits of x in base b |
| RealDigits[x,b,len] | the first len digits of x in base b |
| RealDigits[x,b,len,n] | the first len digits starting with the coefficient of bn |
| FromDigits[list] | construct a number from its decimal digit sequence |
| FromDigits[list,b] | construct a number from its digit sequence in base b |
| FromDigits["string"] | construct an integer from a string of digits |
| FromDigits["string",b] | construct an integer from a string of digits in base b |
| IntegerString[n] | a string of the decimal digits in the integer n |
| IntegerString[n,b] | a string of the digits of n in base b |
This gives a list of digits, together with the number of digits that appear to the left of the decimal point:
| b^^nnnn | a number in base b |
| BaseForm[x,b] | print with x in base b |
| IntegerString[n,b] | a string representing n in base b |
"Output Formats for Numbers" describes how to print numbers in various formats. If you want to create your own formats, you will often need to use MantissaExponent to separate the pieces of real numbers.
| MantissaExponent[x] | give a list containing the mantissa and exponent of x |
| MantissaExponent[x,b] | give the mantissa and exponent in base b |
A standard electronic calculator does all your calculations to a particular accuracy, say ten decimal digits. With the Wolfram Language, however, you can often get exact results.
You can tell the Wolfram Language to give you an approximate numerical result, just as a calculator would, by ending your input with //N. The N stands for "numerical". It must be a capital letter. "Special Ways to Input Expressions" will explain what the // means.
//N always gives the approximate numerical result:
| expr//N | give an approximate numerical value for expr |
When you type in an integer like 7, the Wolfram Language assumes that it is exact. If you type in a number like 4.5, with an explicit decimal point, the Wolfram Language assumes that it is accurate only to a fixed number of decimal places.
Whenever you give a number with an explicit decimal point, the Wolfram Language produces an approximate numerical result:
Here again, the presence of the decimal point makes the Wolfram Language give you an approximate numerical result:
When any number in an arithmetic expression is given with an explicit decimal point, you get an approximate numerical result for the whole expression:
As discussed in "Exact and Approximate Results", the Wolfram Language can handle approximate real numbers with any number of digits. In general, the precision of an approximate real number is the effective number of decimal digits in it which are treated as significant for computations. The accuracy is the effective number of these digits which appear to the right of the decimal point. Note that to achieve full consistency in the treatment of numbers, precision and accuracy often have values that do not correspond to integer numbers of digits.
| Precision[x] | the total number of significant decimal digits in x |
| Accuracy[x] | the number of significant decimal digits to the right of the decimal point in x |
An approximate real number always has some uncertainty in its value, associated with digits beyond those known. One can think of precision as providing a measure of the relative size of this uncertainty. Accuracy gives a measure of the absolute size of the uncertainty.
The Wolfram Language is set up so that if a number 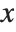 has uncertainty
has uncertainty 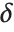 , then its true value can lie anywhere in an interval of size
, then its true value can lie anywhere in an interval of size 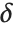 from
from 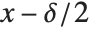 to
to 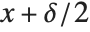 . An approximate number with accuracy
. An approximate number with accuracy 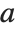 is defined to have uncertainty
is defined to have uncertainty  , while a nonzero approximate number with precision
, while a nonzero approximate number with precision 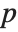 is defined to have uncertainty
is defined to have uncertainty 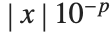 .
.
| N[expr,n] | evaluate expr to n‐digit precision using arbitrary‐precision numbers |
| N[expr] | evaluate expr numerically using machine‐precision numbers |
The Wolfram Language distinguishes two kinds of approximate real numbers: arbitrary‐precision numbers, and machine‐precision numbers or machine numbers. Arbitrary‐precision numbers can contain any number of digits, and maintain information on their precision. Machine numbers, on the other hand, always contain the same number of digits, and maintain no information on their precision.
As discussed in more detail below, machine numbers work by making direct use of the numerical capabilities of your underlying computer system. As a result, computations with them can often be done more quickly. They are however much less flexible than arbitrary‐precision numbers, and difficult numerical analysis can be needed to determine whether results obtained with them are correct.
| MachinePrecision | the precision specification used to indicate machine numbers |
| $MachinePrecision | the effective precision for machine numbers on your computer system |
| MachineNumberQ[x] | test whether x is a machine number |
This returns the symbol MachinePrecision to indicate a machine number:
When you enter an approximate real number, the Wolfram Language has to decide whether to treat it as a machine number or an arbitrary‐precision number. Unless you specify otherwise, if you give fewer than Ceiling[$MachinePrecision+1] digits, the Wolfram Language will treat the number as machine precision, and if you give more digits, it will treat the number as arbitrary precision.
| 123.4 | a machine‐precision number |
| 123.45678901234567890 | an arbitrary‐precision number on some computer systems |
| 123.45678901234567890` | a machine‐precision number on all computer systems |
| 123.456`200 | an arbitrary‐precision number with 200 digits of precision |
| 123.456``200 | an arbitrary‐precision number with 200 digits of accuracy |
| 1.234*^6 | a machine‐precision number in scientific notation (1.234×106) |
| 1.234`200*^6 | a number in scientific notation with 200 digits of precision |
| 2^^101.111`200 | a number in base 2 with 200 binary digits of precision |
| 2^^101.111`200*^6 | a number in base 2 scientific notation (101.1112×26) |
When the Wolfram Language prints out numbers, it usually tries to give them in a form that will be as easy as possible to read. But if you want to take numbers that are printed out by the Wolfram Language, and then later use them as input to the Wolfram Language, you need to make sure that no information gets lost.
In input form, the Wolfram Language explicitly indicates the precision of the number, and gives extra digits to make sure the number can be reconstructed correctly:
| InputForm[expr,NumberMarks->True] | use ` marks in all approximate numbers |
| InputForm[expr,NumberMarks->Automatic] | |
use ` only in arbitrary‐precision numbers | |
| InputForm[expr,NumberMarks->False] | never use ` marks |
The default setting for the NumberMarks option, both in InputForm and in functions such as ToString and OpenWrite is given by the value of $NumberMarks. By resetting $NumberMarks, therefore, you can globally change the way that numbers are printed in InputForm.
In doing numerical computations, it is inevitable that you will sometimes end up with results that are less precise than you want. Particularly when you get numerical results that are very close to zero, you may well want to assume that the results should be exactly zero. The function Chop allows you to replace approximate real numbers that are close to zero by the exact integer 0.
| Chop[expr] | replace all approximate real numbers in expr with magnitude less than 10-10 by 0 |
| Chop[expr,dx] | replace numbers with magnitude less than dx by 0 |
You can get rid of the imaginary part using Chop:
When you use //N to get a numerical result, the Wolfram Language does what a standard calculator would do: it gives you a result to a fixed number of significant figures. You can also tell the Wolfram Language exactly how many significant figures to keep in a particular calculation. This allows you to get numerical results in the Wolfram Language to any degree of precision.
| expr//N or N[expr] | approximate numerical value of expr |
| N[expr,n] | numerical value of expr calculated with n‐digit precision |
This gives the numerical value of 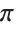 to a fixed number of significant digits. Typing N[Pi] is exactly equivalent to Pi//N:
to a fixed number of significant digits. Typing N[Pi] is exactly equivalent to Pi//N:
Doing any kind of numerical calculation can introduce small roundoff errors into your results. When you increase the numerical precision, these errors typically become correspondingly smaller. Making sure that you get the same answer when you increase numerical precision is often a good way to check your results.
The quantity  turns out to be very close to an integer. To check that the result is not, in fact, an integer, you have to use sufficient numerical precision:
turns out to be very close to an integer. To check that the result is not, in fact, an integer, you have to use sufficient numerical precision:
When you do calculations with arbitrary‐precision numbers, the Wolfram Language keeps track of precision at all points. In general, the Wolfram Language tries to give you results which have the highest possible precision, given the precision of the input you provided.
The Wolfram Language treats arbitrary‐precision numbers as representing the values of quantities where a certain number of digits are known, and the rest are unknown. In general, an arbitrary‐precision number x is taken to have Precision[x] digits which are known exactly, followed by an infinite number of digits which are completely unknown.
When you do a computation, the Wolfram Language keeps track of which digits in your result could be affected by unknown digits in your input. It sets the precision of your result so that no affected digits are ever included. This procedure ensures that all digits returned by the Wolfram Language are correct, whatever the values of the unknown digits may be.
If you give input only to a few digits of precision, the Wolfram Language cannot give you such high‐precision output:
If you want the Wolfram Language to assume that the argument is exactly 142/1000, then you have to say so explicitly:
In many computations, the precision of the results you get progressively degrades as a result of "roundoff error". A typical case of this occurs if you subtract two numbers that are close together. The result you get depends on high‐order digits in each number, and typically has far fewer digits of precision than either of the original numbers.
Adding extra digits in one number but not the other is not sufficient to allow extra digits to be found in the result:
The precision of the output from a function can depend in a complicated way on the precision of the input. Functions that vary rapidly typically give less precise output, since the variation of the output associated with uncertainties in the input is larger. Functions that are close to constants can actually give output that is more precise than their input.
It is worth realizing that different ways of doing the same calculation can end up giving you results with very different precisions. Typically, if you once lose precision in a calculation, it is essentially impossible to regain it; in losing precision, you are effectively losing information about your result.
The fact that different ways of doing the same calculation can give you different numerical answers means, among other things, that comparisons between approximate real numbers must be treated with care. In testing whether two real numbers are "equal", the Wolfram Language effectively finds their difference, and tests whether the result is "consistent with zero" to the precision given.
The internal algorithms that the Wolfram Language uses to evaluate mathematical functions are set up to maintain as much precision as possible. In most cases, built‐in Wolfram Language functions will give you results that have as much precision as can be justified on the basis of your input. In some cases, however, it is simply impractical to do this, and the Wolfram Language will give you results that have lower precision. If you give higher‐precision input, the Wolfram Language will use higher precision in its internal calculations, and you will usually be able to get a higher‐precision result.
| N[expr] | evaluate expr numerically to machine precision |
| N[expr,n] | evaluate expr numerically trying to get a result with n digits of precision |
If you start with an expression that contains only integers and other exact numeric quantities, then N[expr,n] will in almost all cases succeed in giving you a result to n digits of precision. You should realize, however, that to do this the Wolfram Language sometimes has to perform internal intermediate calculations to much higher precision.
The global variable $MaxExtraPrecision specifies how many additional digits should be allowed in such intermediate calculations.
variable | default value | |
| $MaxExtraPrecision | 50 | maximum additional precision to use |
The Wolfram Language automatically increases the precision that it uses internally in order to get the correct answer here:
Using the default setting $MaxExtraPrecision=50, the Wolfram Language cannot get the correct answer here:
This resets $MaxExtraPrecision to its default value:
Even when you are doing computations that give exact results, the Wolfram Language still occasionally uses approximate numbers for some of its internal calculations, so that the value of $MaxExtraPrecision can thus have an effect.
With the default value of $MaxExtraPrecision, the Wolfram Language cannot work this out:
Temporarily resetting $MaxExtraPrecision allows the Wolfram Language to get the result:
In doing calculations that degrade precision, it is possible to end up with numbers that have no significant digits at all. But even in such cases, the Wolfram Language still maintains information on the accuracy of the numbers. Given a number with no significant digits, but accuracy a, the Wolfram Language can then still tell that the actual value of the number must be in the range {-10-a,+10-a}/2. The Wolfram Language by default prints such numbers in the form 0.×10e.
One subtlety in characterizing numbers by their precision is that any number that is consistent with zero must be treated as having zero precision. The reason for this is that such a number has no digits that can be recognized as significant, since all its known digits are just zero.
If you do computations whose results are likely to be near zero, it can be convenient to specify the accuracy, rather than the precision, that you want to get.
| N[expr,p] | evaluate expr to precision p |
| N[expr,{p,a}] | evaluate expr to at most precision p and accuracy a |
| N[expr,{Infinity,a}] | evaluate expr to any precision but to accuracy a |
N cannot guarantee to get a result to precision 20:
When the Wolfram Language works out the potential effect of unknown digits in arbitrary‐precision numbers, it assumes by default that these digits are completely independent in different numbers. While this assumption will never yield too high a precision in a result, it may lead to unnecessary loss of precision.
In particular, if two numbers are generated in the same way in a computation, some of their unknown digits may be equal. Then, when these numbers are, for example, subtracted, the unknown digits may cancel. By assuming that the unknown digits are always independent, however, the Wolfram Language will miss such cancellations.
This quantity has lower precision, since the Wolfram Language assumes that the unknown digits in each number d are independent:
Numerical algorithms sometimes rely on cancellations between unknown digits in different numbers yielding results of higher precision. If you can be sure that certain unknown digits will eventually cancel, then you can explicitly introduce fixed digits in place of the unknown ones. You can carry these fixed digits through your computation, then let them cancel, and get a result of higher precision.
| SetPrecision[x,n] | create a number with n decimal digits of precision, padding with base‐2 zeros if necessary |
| SetAccuracy[x,n] | create a number with n decimal digits of accuracy |
SetPrecision works by adding digits which are zero in base 2. Sometimes, the Wolfram Language stores slightly more digits in an arbitrary‐precision number than it displays, and in such cases, SetPrecision will use these extra digits before introducing zeros.
This creates a number with a precision of 40 decimal digits. The extra digits come from conversion to base 10:
variable | default value | |
| $MaxPrecision | Infinity | maximum total precision to be used |
| $MinPrecision | 0 | minimum precision to be used |
By making the global assignment $MinPrecision=n, you can effectively apply SetPrecision[expr,n] at every step in a computation. This means that even when the number of correct digits in an arbitrary‐precision number drops below n, the number will always be padded to have n digits.
If you set $MaxPrecision=n as well as $MinPrecision=n, then you can force all arbitrary‐precision numbers to have a fixed precision of n digits. In effect, what this does is to make the Wolfram Language treat arbitrary‐precision numbers in much the same way as it treats machine numbers—but with more digits of precision.
Fixed‐precision computation can make some calculations more efficient, but without careful analysis you can never be sure how many digits are correct in the results you get.
Whenever machine‐precision numbers appear in a calculation, the whole calculation is typically done in machine precision. The Wolfram Language will then give machine‐precision numbers as the result.
Whenever the input contains any machine‐precision numbers, the Wolfram Language does the computation to machine precision:
When you do calculations with arbitrary‐precision numbers, as discussed in "Arbitrary‐Precision Numbers", the Wolfram Language always keeps track of the precision of your results, and gives only those digits which are known to be correct, given the precision of your input. When you do calculations with machine‐precision numbers, however, the Wolfram Language always gives you a machine‐precision result, whether or not all the digits in the result can, in fact, be determined to be correct on the basis of your input.
The fact that you can get spurious digits in machine‐precision numerical calculations with the Wolfram Language is in many respects quite unsatisfactory. The ultimate reason, however, that the Wolfram Language uses fixed precision for these calculations is a matter of computational efficiency.
The Wolfram Language is usually set up to insulate you as much as possible from the details of the computer system you are using. In dealing with machine‐precision numbers, you would lose too much, however, if the Wolfram Language did not make use of some specific features of your computer.
The important point is that almost all computers have special hardware or microcode for doing floating‐point calculations to a particular fixed precision. The Wolfram Language makes use of these features when doing machine‐precision numerical calculations.
The typical arrangement is that all machine‐precision numbers in the Wolfram Language are represented as "double‐precision floating‐point numbers" in the underlying computer system. On most current computers, such numbers contain a total of 64 binary bits, typically yielding 16 decimal digits of mantissa.
The main advantage of using the built‐in floating‐point capabilities of your computer is speed. Arbitrary‐precision numerical calculations, which do not make such direct use of these capabilities, are usually many times slower than machine‐precision calculations.
There are several disadvantages of using built‐in floating‐point capabilities. One already mentioned is that it forces all numbers to have a fixed precision, independent of what precision can be justified for them.
A second disadvantage is that the treatment of machine‐precision numbers can vary slightly from one computer system to another. In working with machine‐precision numbers, the Wolfram Language is at the mercy of the floating‐point arithmetic system of each particular computer. If floating‐point arithmetic is done differently on two computers, you may get slightly different results for machine‐precision Wolfram Language calculations on those computers.
| $MachinePrecision | the number of decimal digits of precision |
| $MachineEpsilon | the minimum positive machine‐precision number which can be added to 1.0 to give a result distinguishable from 1.0 |
| $MaxMachineNumber | the maximum machine‐precision number |
| $MinMachineNumber | the minimum positive machine‐precision number that can be represented in normalized form |
| $MaxNumber | the maximum magnitude of an arbitrary‐precision number |
| $MinNumber | the minimum magnitude of a positive arbitrary‐precision number |
Since machine‐precision numbers on any particular computer system are represented by a definite number of binary bits, numbers that are too close together will have the same bit pattern, and so cannot be distinguished. The parameter $MachineEpsilon gives the distance between 1.0 and the closest number that has a distinct binary representation.
This gives the value of $MachineEpsilon for the computer system on which these examples are run:
InputForm reveals that the result is not exactly 1:
Subtracting 1 gives $MachineEpsilon:
Machine numbers have not only limited precision, but also limited magnitude. If you generate a number that is larger in magnitude than $MaxMachineNumber, the Wolfram Language will automatically convert the number to arbitrary‐precision form.
This is the maximum machine‐precision number that can be handled on the computer system used for this example:
The Wolfram Language automatically converts any result larger than $MaxMachineNumber to arbitrary precision:
As of Version 11.3, if a machine-precision computation generates a number that is smaller in magnitude than $MinMachineNumber, the Wolfram Language will issue a warning. However, it will retain the result as a subnormal machine number that has leading zeros in its binary significand.
This is the minimum machine‐precision number that can be put into normal form on the computer system used for this example:
The Wolfram Language issues warnings about computations that produce numbers smaller than $MinMachineNumber, but it does not automatically convert to arbitrary-precision arithmetic:
Converting to arbitrary precision using SetPrecision can avoid this underflow:
| Interval[{min,max}] | the interval from min to max |
| Interval[{min1,max1},{min2,max2},…] | |
the union of intervals from min1 to max1, min2 to max2, … | |
Abs folds the intervals back together again:
| IntervalUnion[interval1,interval2,…] | find the union of several intervals |
| IntervalIntersection[interval1,interval2,…] | |
find the intersection of several intervals | |
| IntervalMemberQ[interval,x] | test whether the point x lies within an interval |
| IntervalMemberQ[interval1,interval2] | test whether interval2 lies completely within interval1 |
You can use intervals not only with exact quantities but also with approximate numbers. Even with machine‐precision numbers, the Wolfram Language always tries to do rounding in such a way as to preserve the validity of results.
This shows explicitly the interval treated by the Wolfram Language as the machine‐precision number 0.
If you type in an expression like 0/0, the Wolfram Language prints a message, and returns the result Indeterminate:
An expression like 0/0 is an example of an indeterminate numerical result. If you type in 0/0, there is no way for the Wolfram Language to know what answer you want. If you got 0/0 by taking the limit of 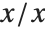 as
as  , then you might want the answer 1. On the other hand, if you got 0/0 instead as the limit of
, then you might want the answer 1. On the other hand, if you got 0/0 instead as the limit of 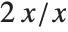 , then you probably want the answer 2. The expression 0/0 on its own does not contain enough information to choose between these and other cases. As a result, its value must be considered indeterminate.
, then you probably want the answer 2. The expression 0/0 on its own does not contain enough information to choose between these and other cases. As a result, its value must be considered indeterminate.
Whenever an indeterminate result is produced in an arithmetic computation, the Wolfram Language prints a warning message, and then returns Indeterminate as the result of the computation. If you ever try to use Indeterminate in an arithmetic computation, you always get the result Indeterminate. A single indeterminate expression effectively "poisons" any arithmetic computation. (The symbol Indeterminate plays a role in the Wolfram Language similar to the "not a number" object in the IEEE Floating Point Standard.)
The usual laws of arithmetic simplification are suspended in the case of Indeterminate:
Indeterminate "poisons" any arithmetic computation, and leads to an indeterminate result:
When you do arithmetic computations inside Wolfram Language programs, it is often important to be able to tell whether indeterminate results were generated in the computations. You can do this by using the function Check discussed in "Messages" to test whether any warning messages associated with indeterminate results were produced.
You can use Check inside a program to test whether warning messages are generated in a computation:
| Indeterminate | an indeterminate numerical result |
| Infinity | a positive infinite quantity |
| -Infinity | |
| DirectedInfinity[r] | an infinite quantity with complex direction r |
| ComplexInfinity | an infinite quantity with an undetermined direction |
| DirectedInfinity[] | equivalent to ComplexInfinity |
There are many situations where it is convenient to be able to do calculations with infinite quantities. The symbol Infinity in the Wolfram Language represents a positive infinite quantity. You can use it to specify such things as limits of sums and integrals. You can also do some arithmetic calculations with it.
There are a number of subtle points that arise in handling infinite quantities. One of them concerns the "direction" of an infinite quantity. When you do an infinite integral, you typically think of performing the integration along a path in the complex plane that goes to infinity in some direction. In this case, it is important to distinguish different versions of infinity that correspond to different directions in the complex plane.  and
and  are two examples, but for some purposes one also needs
are two examples, but for some purposes one also needs  and so on.
and so on.
In the Wolfram Language, infinite quantities can have a "direction", specified by a complex number. When you type in the symbol Infinity, representing a positive infinite quantity, this is converted internally to the form DirectedInfinity[1], which represents an infinite quantity in the 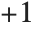 direction. Similarly, -Infinity becomes DirectedInfinity[-1], and IInfinity becomes DirectedInfinity[I]. Although the DirectedInfinity form is always used internally, the standard output format for DirectedInfinity[r] is r Infinity.
direction. Similarly, -Infinity becomes DirectedInfinity[-1], and IInfinity becomes DirectedInfinity[I]. Although the DirectedInfinity form is always used internally, the standard output format for DirectedInfinity[r] is r Infinity.
Although the notion of a "directed infinity" is often useful, it is not always available. If you type in 1/0, you get an infinite result, but there is no way to determine the "direction" of the infinity. The Wolfram Language represents the result of 1/0 as DirectedInfinity[]. In standard output form, this undirected infinity is printed out as ComplexInfinity.
| NHoldAll | prevent any arguments of a function from being affected by N |
| NHoldFirst | prevent the first argument from being affected |
| NHoldRest | prevent all but the first argument from being affected |
Usually N goes inside functions and gets applied to each of their arguments: