BoundaryUnitNormal
BoundaryUnitNormal[x,y,…]
領域に対して外向きの単位法線ベクトル ![]() を表す.
を表す.
詳細とオプション
- BoundaryUnitNormalは,境界の単位法線ベクトル
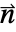 に従属する,偏微分方程式の境界条件を構築するために使える.
に従属する,偏微分方程式の境界条件を構築するために使える. - BoundaryUnitNormalは,NeumannValue,DirichletCondition,NIntegrateと一緒に使える.
- BoundaryUnitNormalは,AcousticAbsorbingValue,HeatFluxValue,MassOutflowValue等の境界条件によって生成できる.
- BoundaryUnitNormalは,境界上の接線を指定するために使える.
- BoundaryUnitNormalは,境界条件が離散化される場合には,領域
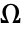 の埋込み次元の長さのベクトルに評価する.
の埋込み次元の長さのベクトルに評価する. - 境界の単位法線成分
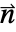 には,Indexedを使ってアクセスできる.
には,Indexedを使ってアクセスできる. - 有限要素の近似には,偏微分方程式に検定関数
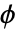 が掛けられ,
が掛けられ,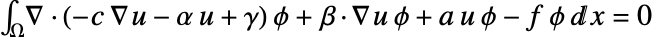 上で積分される.部分積分で
上で積分される.部分積分で 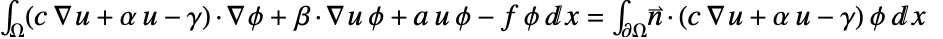 が得られる.境界の積分における被積分関数
が得られる.境界の積分における被積分関数 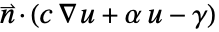 は,NeumannValueの
は,NeumannValueの 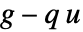 で置き換えられる.
で置き換えられる. - 偏微分方程式がノイマン値を
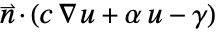 と指定する場合には,NeumannValueを
と指定する場合には,NeumannValueを 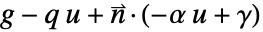 と指定することによって,代りにBoundaryUnitNormalを使って
と指定することによって,代りにBoundaryUnitNormalを使って 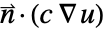 をモデル化することができる.
をモデル化することができる. - 逆に,偏微分方程式がノイマン値を
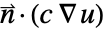 と指定する場合には,NeumannValueを
と指定する場合には,NeumannValueを 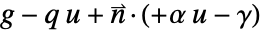 と指定することによって,代りにBoundaryUnitNormalを使って
と指定することによって,代りにBoundaryUnitNormalを使って 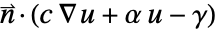 をモデル化することができる.
をモデル化することができる. - 領域の内部境界においては,境界の単位法線成分は一意的には定義されない.
- 境界の単位法線の値
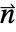 は,領域
は,領域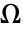 全体で内部境界を含むすべての境界について,
全体で内部境界を含むすべての境界について,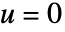 のディリクレ条件で
のディリクレ条件で 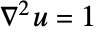 を解くことによって計算される.すると,境界の単位法線成分は
を解くことによって計算される.すると,境界の単位法線成分は 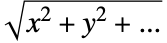 で正規化された
で正規化された 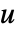 の勾配になる.
の勾配になる.
例題
すべて開くすべて閉じる例 (1)
スコープ (6)
単位Diskについてポワソン方程式を解く:
領域の境界を通る流束の合計を,境界領域の二次近似で計算する:
左に,境界の単位法線成分でNeumannValueを設定し,方程式を解く:
この範囲について,左のBoundaryUnitNormalの等価は![]() である:
である:
NeumannValueについて接線成分を作成する:
BoundaryUnitNormalのIndexed成分を利用してNeumannValueを計算する:
境界の法線成分でNeumannValueを設定する:
アプリケーション (1)
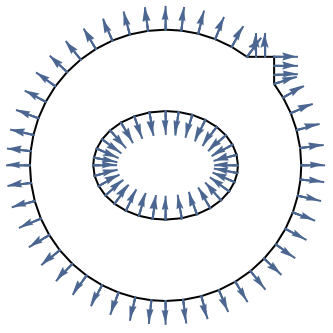
以下の例では,環帯領域において指定された表面力境界条件を持つストークス流を考える.辺の外側では ![]() において粘着境界条件が存在する.これらが
において粘着境界条件が存在する.これらが ![]() と
と ![]() の方向での流速を0,つまり
の方向での流速を0,つまり ![]() に設定する.内側の境界では
に設定する.内側の境界では ![]() において表面力が指定される.応力ベクトル
において表面力が指定される.応力ベクトル ![]() の表面力は以下で与えられる:
の表面力は以下で与えられる:
ここでは,![]() は
は ![]() として与えられる動径単位ベクトルであり,
として与えられる動径単位ベクトルであり,![]() は
は ![]() として与えられる接線単位ベクトルである.
として与えられる接線単位ベクトルである. ![]() と
と ![]() はそれぞれ
はそれぞれ ![]() と
と ![]() の方向でのデカルト単位ベクトルである.この例では,表面力は法線方向には
の方向でのデカルト単位ベクトルである.この例では,表面力は法線方向には ![]() ,接線成分の表面力は
,接線成分の表面力は ![]() に設定される.言い換えれば,内側の境界では,速度は指定されず,表面力
に設定される.言い換えれば,内側の境界では,速度は指定されず,表面力 ![]() のみが指定される.
のみが指定される.
内側の表面では,外向きの単位法線 ![]() とクロス積から接線単位法線を計算することができる.クロス積を使って,単位法線ベクトル
とクロス積から接線単位法線を計算することができる.クロス積を使って,単位法線ベクトル ![]() から単位接線を計算する:
から単位接線を計算する:
![]() と
と ![]() の方向それぞれについてクロス積の第1成分と第2成分を抽出するためには,Indexedを使う.
の方向それぞれについてクロス積の第1成分と第2成分を抽出するためには,Indexedを使う.
接線単位法線も同じように ![]() として与えられることが可能であることに注意する.内側の表面の単位法線ベクトルは
として与えられることが可能であることに注意する.内側の表面の単位法線ベクトルは ![]() であり,すると単位接線は
であり,すると単位接線は ![]() になるからである:
になるからである:
圧力に対する境界条件を指定しなければ,圧力値が浮いてしまい,NDSolveは十分な境界条件が指定されていないと警告を発する:
表面力境界条件がうまく使えることを確かめるためには,速度の動径成分と接線成分を計算し,それらを ![]() においてすべての
においてすべての ![]() についてプロットすることができる.動径速度については
についてプロットすることができる.動径速度については ![]() に比例する解が期待され,接線速度については
に比例する解が期待され,接線速度については ![]() に比例する解が期待される.
に比例する解が期待される.
次に内側の境界での法線応力と剪断応力を計算し,それらが指定された表面力境界条件と一致することを確かめる.応力テンソルは以下で与えられる:
特性と関係 (2)
境界単位法線は,領域上でポワソン方程式を解き,ゼロディリクレ条件を指定することによって計算される.単位Disk上でのポワソン方程式を計算する:
これは,ElementMeshの境界単位法線を計算することと同じである:
テキスト
Wolfram Research (2023), BoundaryUnitNormal, Wolfram言語関数, https://reference.wolfram.com/language/FEMDocumentation/ref/BoundaryUnitNormal.html.
CMS
Wolfram Language. 2023. "BoundaryUnitNormal." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/FEMDocumentation/ref/BoundaryUnitNormal.html.
APA
Wolfram Language. (2023). BoundaryUnitNormal. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/FEMDocumentation/ref/BoundaryUnitNormal.html