WOLFRAM

Wolfram Language & System Documentation Center
Wolfram Language Home Page »
NDSolve`FEM`
NDSolve`FEM`

InitializePDEMethodData

InitializePDEMethodData[vd,sd,m]

returns a method data object for the method specified by m according to variable data vd and solution data sd.

Details and Options

  • InitializePDEMethodData initializes the PDE discretization method m.
  • InitializePDEMethodData computes and stores data such as geometry data.
  • The Automatic method for InitializePDEMethodData is the finite element method and the initialized data is returned as a FEMMethodData object.
  • Variable data vd and solution data sd are corresponding lists of variables and values. Templates for vd and sd may be generated using NDSolve`VariableData and NDSolve`SolutionData, and components may be set using NDSolve`SetSolutionDataComponent.
  • The "Space" component of vd and sd should be set to the spatial variables and the spatial mesh represented as an NumericalRegion object, respectively.
  • The "DependentVariables" component of vd should be set to the list of unknown function names without arguments.
  • For time-dependent problems, the "Time" component of vd and sd should be set to the temporal variable and the initial time, respectively.
  • In InitializePDEMethodData[vd,sd,m], the method m may be specified by mname or {mname,mopts}, where mname is the method name and mopts are method specific options. Currently only the "FiniteElement" method is supported.
  • InitializePDEMethodData[vd,sd] uses the "FiniteElement" method by default.
  • The "FiniteElement" method accepts the following options:
  • "IntegrationOrder" Automaticsets the element integration order
    "InterpolationOrder" Automaticsets the order of interpolation for each dependent variable
    "MeshOptions" Automaticspecifies options for mesh generation
    "PrecomputeGeometryData" Automaticprecomputes geometry data
  • With an ElementMesh having "MeshOrder" 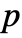p, the "InterpolationOrder" can be at most 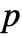p and "InterpolationOrder"->Automatic defaults to the order 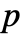p. Multiple dependent variables may have a different interpolation order; at least one interpolation order needs to be set to the maximum mesh order p.
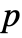  • The "IntegrationOrder" is the order of accuracy used to integrate the finite element operators. For "InterpolationOrder"->2, the "IntegrationOrder" defaults to fourth order and for "InterpolationOrder"->1, the "IntegrationOrder" defaults to second order.
  • For the "FiniteElement" method, if the NumericalRegion does not contain an ElementMesh, then one is created automatically using ToElementMesh, with the options given in the setting of "MeshOptions".
  • Setting the option from NDSolve and related functions is explained in NDSolve Finite Element Options.

Examples

open allclose all

Basic Examples  (1)Summary of the most common use cases

Load the finite element package:

In[1]:=1
✖
https://wolfram.com/xid/0cm68ddr75ate6h0pj25a6ok6zvluq-j4klzi

Set up a NumericalRegion:

In[2]:=2
✖
https://wolfram.com/xid/0cm68ddr75ate6h0pj25a6ok6zvluq-nx6wf8
Out[2]=2

Set up variable and solution data:

In[3]:=3
✖
https://wolfram.com/xid/0cm68ddr75ate6h0pj25a6ok6zvluq-b1fv3m

Initialize the partial differential equation data:

In[4]:=4
✖
https://wolfram.com/xid/0cm68ddr75ate6h0pj25a6ok6zvluq-bly9dw
Out[4]=4

Options  (5)Common values & functionality for each option

"IntegrationOrder"  (1)

The integration order is a submethod option for the finite element method that specifies the numerical integration order used by the method.

Set the integration order to 2:

In[1]:=1
✖
https://wolfram.com/xid/0cm68ddr75ate6h0pj25a6ok6zvluq-vq1zpt
Out[1]=1

In the case where an ElementMesh with "MeshOrder" 2 is given, the Automatic setting chooses an integration order of 4. For an ElementMesh with "MeshOrder" 1, an integration order of 2 is chosen. The maximum order is 5.

"InterpolationOrder"  (1)

The interpolation order is a submethod for the finite element method option and specifies the interpolation order for each dependent variable:

In[1]:=1
✖
https://wolfram.com/xid/0cm68ddr75ate6h0pj25a6ok6zvluq-td02yr

Specify that the dependent variable u is to be interpolated as second order, while the dependent variable v is interpolated with first order:

In[2]:=2
✖
https://wolfram.com/xid/0cm68ddr75ate6h0pj25a6ok6zvluq-kzbmbu
Out[2]=2

"MeshOptions"  (1)

"MeshOptions" is a submethod option for the finite element method that specifies the options to be passed to ToElementMesh.

Initialize the partial differential equation data with a first-order mesh:

In[1]:=1
✖
https://wolfram.com/xid/0cm68ddr75ate6h0pj25a6ok6zvluq-d0tcur
Out[1]=1

Inspect the mesh order in the numerical region:

In[2]:=2
✖
https://wolfram.com/xid/0cm68ddr75ate6h0pj25a6ok6zvluq-r0jrtq
Out[2]=2

Method  (1)

The default method uses a finite element method:

In[1]:=1
✖
https://wolfram.com/xid/0cm68ddr75ate6h0pj25a6ok6zvluq-ow7zh4
Out[1]=1

"PrecomputeGeometryData"  (1)

Precomputing geometry data is a submethod option for the finite element method that computes and stores geometry data needed by the method. Setting this to False may save some memory:

In[1]:=1
✖
https://wolfram.com/xid/0cm68ddr75ate6h0pj25a6ok6zvluq-usmxei
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0cm68ddr75ate6h0pj25a6ok6zvluq-mfnwej
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0cm68ddr75ate6h0pj25a6ok6zvluq-kycv84
Out[3]=3
Out[3]=3
Wolfram Research (2014), InitializePDEMethodData, Wolfram Language function, https://reference.wolfram.com/language/FEMDocumentation/ref/InitializePDEMethodData.html (updated 2020).
✖
Wolfram Research (2014), InitializePDEMethodData, Wolfram Language function, https://reference.wolfram.com/language/FEMDocumentation/ref/InitializePDEMethodData.html (updated 2020).

Text

Wolfram Research (2014), InitializePDEMethodData, Wolfram Language function, https://reference.wolfram.com/language/FEMDocumentation/ref/InitializePDEMethodData.html (updated 2020).

✖
Wolfram Research (2014), InitializePDEMethodData, Wolfram Language function, https://reference.wolfram.com/language/FEMDocumentation/ref/InitializePDEMethodData.html (updated 2020).

CMS

Wolfram Language. 2014. "InitializePDEMethodData." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2020. https://reference.wolfram.com/language/FEMDocumentation/ref/InitializePDEMethodData.html.

✖
Wolfram Language. 2014. "InitializePDEMethodData." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2020. https://reference.wolfram.com/language/FEMDocumentation/ref/InitializePDEMethodData.html.

APA

Wolfram Language. (2014). InitializePDEMethodData. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/FEMDocumentation/ref/InitializePDEMethodData.html

✖
Wolfram Language. (2014). InitializePDEMethodData. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/FEMDocumentation/ref/InitializePDEMethodData.html

BibTeX

@misc{reference.wolfram_2025_initializepdemethoddata, author="Wolfram Research", title="{InitializePDEMethodData}", year="2020", howpublished="\url{https://reference.wolfram.com/language/FEMDocumentation/ref/InitializePDEMethodData.html}", note=[Accessed: 26-March-2025 ]}

✖
@misc{reference.wolfram_2025_initializepdemethoddata, author="Wolfram Research", title="{InitializePDEMethodData}", year="2020", howpublished="\url{https://reference.wolfram.com/language/FEMDocumentation/ref/InitializePDEMethodData.html}", note=[Accessed: 26-March-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_initializepdemethoddata, organization={Wolfram Research}, title={InitializePDEMethodData}, year={2020}, url={https://reference.wolfram.com/language/FEMDocumentation/ref/InitializePDEMethodData.html}, note=[Accessed: 26-March-2025 ]}

✖
@online{reference.wolfram_2025_initializepdemethoddata, organization={Wolfram Research}, title={InitializePDEMethodData}, year={2020}, url={https://reference.wolfram.com/language/FEMDocumentation/ref/InitializePDEMethodData.html}, note=[Accessed: 26-March-2025 ]}