MultivariateStatistics`
MultivariateStatistics`

HotellingTSquareDistribution

As of Version 8, HotellingTSquareDistribution is part of the built-in Wolfram Language kernel.

HotellingTSquareDistribution[p,m]

represents Hotelling's distribution with dimensionality parameter p and degrees of freedom parameter m.

Details and Options

  • To use HotellingTSquareDistribution, you first need to load the Multivariate Statistics Package using Needs["MultivariateStatistics`"].
  • HotellingTSquareDistribution is a univariate distribution derived from the multivariate normal distribution.
  • The probability density for value x in Hotelling's 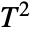distribution is proportional to x-1+p/2(1+x/m)-(m+1)/2 for x>0.
  • The parameters p and m can be any positive real numbers such that m>p-1.
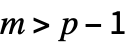  • HotellingTSquareDistribution can be used with such functions as Mean, CDF, and RandomReal.

Examples

open allclose all

Basic Examples  (3)

The mean of a Hotelling distribution:

The variance:

Probability density function:

Scope  (3)

Generate a set of pseudorandom numbers that follow a Hotelling distribution:

Properties & Relations  (1)

The probability density function integrates to unity:

Hotelling variables are related to F-ratio variables by a multiplicative constant:

Possible Issues  (2)

HotellingTSquareDistribution is not defined when m<p:

HotellingTSquareDistribution is not defined when p is less than 0:

Substitution of invalid parameters into symbolic outputs gives results that are not meaningful:

Wolfram Research (2007), HotellingTSquareDistribution, Wolfram Language function, https://reference.wolfram.com/language/MultivariateStatistics/ref/HotellingTSquareDistribution.html.

Text

Wolfram Research (2007), HotellingTSquareDistribution, Wolfram Language function, https://reference.wolfram.com/language/MultivariateStatistics/ref/HotellingTSquareDistribution.html.

CMS

Wolfram Language. 2007. "HotellingTSquareDistribution." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/MultivariateStatistics/ref/HotellingTSquareDistribution.html.

APA

Wolfram Language. (2007). HotellingTSquareDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/MultivariateStatistics/ref/HotellingTSquareDistribution.html

BibTeX

@misc{reference.wolfram_2024_hotellingtsquaredistribution, author="Wolfram Research", title="{HotellingTSquareDistribution}", year="2007", howpublished="\url{https://reference.wolfram.com/language/MultivariateStatistics/ref/HotellingTSquareDistribution.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_hotellingtsquaredistribution, organization={Wolfram Research}, title={HotellingTSquareDistribution}, year={2007}, url={https://reference.wolfram.com/language/MultivariateStatistics/ref/HotellingTSquareDistribution.html}, note=[Accessed: 21-November-2024 ]}