MultivariateStatistics`
MultivariateStatistics`

MultivariateTDistribution

As of Version 8, MultivariateTDistribution is part of the built-in Wolfram Language kernel.

MultivariateTDistribution[Σ,m]

represents the multivariate Student distribution with scale matrix Σ and degrees of freedom parameter m.

MultivariateTDistribution[μ,Σ,m]

represents the multivariate Student distribution with location μ, scale matrix Σ, and m degrees of freedom.

Details and Options

  • To use MultivariateTDistribution, you first need to load the Multivariate Statistics Package using Needs["MultivariateStatistics`"].
  • The probability density for vector x in a multivariate t distribution is proportional to (1+(x-μ).Σ-1.(x-μ)/m)-(m+Length[Σ])/2.
  • The scale matrix Σ can be any real‐valued symmetric positive definite matrix.
  • With specified location μ, μ can be any vector of real numbers, and Σ can be any symmetric positive definite p×p matrix with p=Length[μ].
  • The multivariate Student 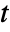distribution characterizes the ratio of a multinormal to the covariance between the variates.
  • MultivariateTDistribution can be used with such functions as Mean, CDF, and RandomReal.

Examples

open allclose all

Basic Examples  (3)

The mean of a bivariate distribution with 10 degrees of freedom:

The variances of each dimension:

Probability density function:

Scope  (3)

Generate a set of pseudorandom vectors that follow a trivariate distribution:

Applications  (1)

Equal probability contours for a bivariate distribution:

Properties & Relations  (1)

The probability density function integrates to unity:

Possible Issues  (2)

MultivariateTDistribution is not defined when Σ is not a symmetric positive definite matrix:

MultivariateTDistribution is not defined when m is not positive:

Substitution of invalid parameters into symbolic outputs gives results that are not meaningful:

Wolfram Research (2007), MultivariateTDistribution, Wolfram Language function, https://reference.wolfram.com/language/MultivariateStatistics/ref/MultivariateTDistribution.html (updated 2008).

Text

Wolfram Research (2007), MultivariateTDistribution, Wolfram Language function, https://reference.wolfram.com/language/MultivariateStatistics/ref/MultivariateTDistribution.html (updated 2008).

CMS

Wolfram Language. 2007. "MultivariateTDistribution." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2008. https://reference.wolfram.com/language/MultivariateStatistics/ref/MultivariateTDistribution.html.

APA

Wolfram Language. (2007). MultivariateTDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/MultivariateStatistics/ref/MultivariateTDistribution.html

BibTeX

@misc{reference.wolfram_2024_multivariatetdistribution, author="Wolfram Research", title="{MultivariateTDistribution}", year="2008", howpublished="\url{https://reference.wolfram.com/language/MultivariateStatistics/ref/MultivariateTDistribution.html}", note=[Accessed: 08-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_multivariatetdistribution, organization={Wolfram Research}, title={MultivariateTDistribution}, year={2008}, url={https://reference.wolfram.com/language/MultivariateStatistics/ref/MultivariateTDistribution.html}, note=[Accessed: 08-November-2024 ]}