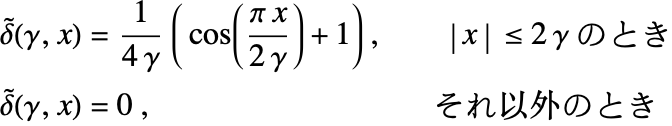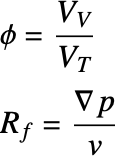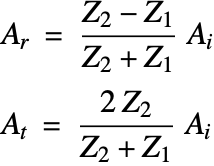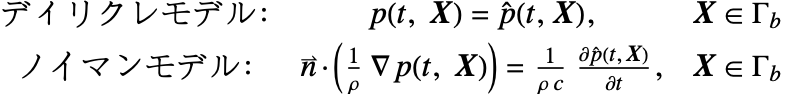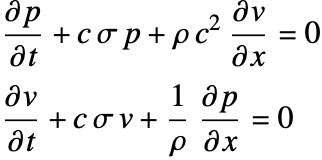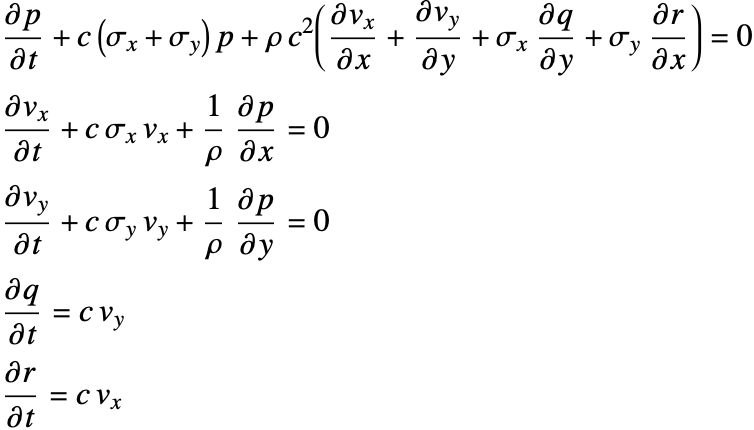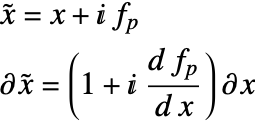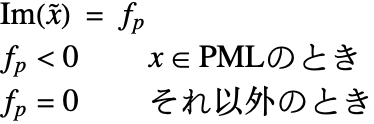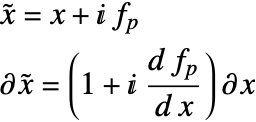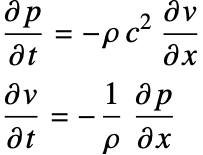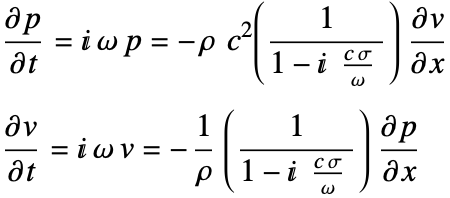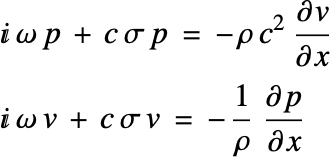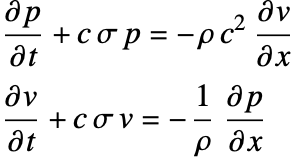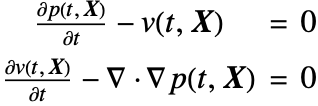はじめに

音響学とは圧力の変化によって音をモデル化する物理の一領域である．圧力の変化は波動方程式によって説明できる．このチュートリアルは時間領域における波動方程式で音をモデル化する取り掛かりとなるものであり，モデリング過程のさまざまな面を提示する．モデリングの過程は結果的に，NDSolveで解くことができる偏微分方程式(PDE)モデルとなる．さらにいろいろななタイプの音源の他，利用可能なPDEの境界条件を使ってどのように実世界の音の障壁をモデル化できるかについての概要を説明する．

このチュートリアルでは時間領域モデリングを使って，音波が時間においてどのように振る舞うかを調べる．音は周波数領域でモデル化することもできる．モデリングに周波数領域を使うことで，周波数領域場で音波がどのように分布するかが示される．周波数領域モデリングは，ノイズフィルタ等の周波数依存の音響系を解析する際によく使われる．

周波数領域における音のモデリングの詳細は，別のチュートリアル「周波数領域における音響学」でご覧いただきたい．

音響系モデリングの拡張例題はモデルコレクションで見ることができる．

このノートブックに掲載されているシミュレーション結果のアニメーションの多くは，Rasterizeの呼出しで生成される．これは，このノートブックが必要とするディスク容量を減少させるためである．欠点は，アニメーションの見栄えが呼出しがない場合ほどはっきりとしないことである．高品質のグラフィックスを得るためには，Rasterizeの呼出しを削除するかコメントアウトするかするとよい．

このチュートリアルで使われる記号とその単位は，用語集のセクションに要約されている．

波動方程式

波動方程式の基本

波動方程式(1)は，無損失媒体における音の時間依存（過渡的）伝搬をモデル化するために使われる：

波動方程式の従属変数は音圧 である．音圧は密度 の媒体の中で音速 で伝搬する．音圧は周囲の基準圧力 からの局所圧力偏差として理解することができる．圧力 は時間 と位置 によって異なる．項 および はそれぞれ単極音源と二重極音源である．これらの音源については音源タイプで説明する．

音は質量運搬なしですべての形式の物質を通して伝搬し，通常波の伝搬の方向に沿って媒体の音圧を変えることによって縦波として伝達される．固体の媒体の場合，音は縦に伝達され，それに加え波が伝搬の方向に垂直に振動するように横にも伝達される[2]．次のアニメーションは縦波と横波の粒子運動を示す[3]．

このアニメーションはハイライトされた粒子が縦波上で水平に振動するが，横波上では垂直に上下する様子を示す．

ドキュメントのさまざまなセクションで非アクティブな偏微分方程式演算子の使い方が説明されている．詳細は「偏微分方程式の数値解法」をご覧いただきたい．

実際の数値的材料パラメータは置換を使ってモデルに挿入する．

モデルパラメータの設定

音波は，その時間依存の形式によって2つに分類することができる．時間調和波は単独の周波数で正弦的時間変動を持つ．時間非調和波は複数の周波数で任意の時間変動を持つ．

音響学的シミュレーションでは，音波の波長 は，支配PDEの正確な数値解を得るために，十分に細かいメッシュで解く必要がある．ここでは時間調和波および時間非調和波の両方について最大のセル寸法を設定する関数を作成する．

このチュートリアルでは，時間調和波には特定の例の周波数を，時間非調和波の例としてはガウスパルスを使う．

最大辺長のデフォルトの解像度は波長 について12ノードに設定される．つまり波の伝播の各方向において波長 につき少なくとも12個の要素があるということである．通常これは波を正しく解像するのに十分である[4]が，異なる正確さが要求された場合には別の解像値を割り当てることもできる．

波長 は時間調和波と時間非調和波とで計算方法が異なる．時間調和波の場合は か であり，ここで周波数 は により角周波数 に関連している．時間非調和波の場合は であり， はガウスパルスの標準偏差である[5]．

次のモデルパラメータはこのチュートリアルの例で使われる．これらのパラメータはシユレーション領域とシミュレーションの終了時間 を定義する．

音響波が不かく乱領域で始まる場合，初期の音圧 とその導関数はゼロに設定される．

時間非調和波の例では，通常標準偏差 のガウスパルスを使う．

多くの例で，波の反射を避けるために吸収境界条件(ABC)を使う．

音波のタイプ

音波はその時間依存性の形式によって2つに分類できる．時間調和波は単一の周波数の正弦曲線の時間変化を持つ．時間非調和波は複数の周波数の任意の時間変化を持つ．

単一の周波数 および時間について正弦曲線の変化に依存する音波は時間調和波といわれ，(6)で与えられる：

ここで は音圧振幅の空間分布を表す．

任意波は離散周波数を持つ調和波の無限和に分解することができる[7]．この処理は周波数解析と呼ばれる．人間の耳や騒音制御器等の多くの音響系は周波数依存なので，ほとんどの音響解析には周波数解析が関係する．周波数解析の基本である調和波挙動は音響工学における根本的なトピックである．

時間調和波は複雑な指数表現で表されることが多い．

調和空間依存を持つ音波では，振幅関数は以下のようになる．

ここで は調和的に振動する数量の振幅であり， は音波数で単位距離あたりの位相変化として解釈される．

の指数の変数 は波の移動の向きを定義する．と設定することで波は負の 方向に伝搬し， と設定すると正の 方向に伝搬する．

(8)と(9)を合わせると，移動する時間調和波は次のように表すことができる．

このアニメーションには，時間 のスライダー，向きのスイッチ ，周波数 および波数 のセレクターの4つのモデルパラメータがある．高い周波数 を選ぶと，単位時間あたりの位相変化の数が増加する．波数 が増加するに連れて単位距離あたりの位相変化の数は増加する．時間 のスライダーを動かすことによって波の伝搬を観察することができる．

がsource free波動方程式(10)に代入されると，この方程式は時間非依存の二階微分方程式である非同次ヘルムホルツ方程式に簡約される：

波源がない場合，この偏微分方程式系は，NDEigensystemで解くことのできる固有値問題になる．この固有値の集合によって，対応する音響系の自然周波数が決められる．

ホルムヘルツ方程式を使った音のモデリングの詳細は，「周波数領域における音響学」でご覧いただきたい．

次に波動方程式(11)を使って1Dの時間調和波モデルを構築し，NDSolveValueを使って数値的に解く．

時間非調和波は任意の時間変化を持ち，以下で表されることがある．

ここで は任意関数であり，その引数は波動方程式(12)を満足するために形式 を持つ．ここでも に何を選ぶかで波の移動方向が定義される．と設定すると波は負の 方向に伝搬し，と設定すると正の 方向に伝搬する．

このアニメーションには，時間 のスライダー，方向スイッチ ，音速 のセレクターの3つのモデルパラメータがある．時間 のスライダーを動かすことで波の伝搬を観察することができる．

次に波動方程式(13)を使って1Dの時間非調和波のモデルを構築し，NDSolveValueを使って数値的に解く．

このアニメーションから時間非調和波上の点には任意の時間変化があることが分かる．

音源のタイプ

波動方程式モデル(14)は単極音源と二重極音源の2つのタイプの時間調和音源を含んでいる．単極音源 は音を等方的に放射する点光源をモデル化する．これに対して二重極音源 は，反対の位相であり，音の波長と比較して距離 だけ離れた2つの等しい単極音源からなる．

波動方程式(15)の単極音源 は音を等方的に放射する点光源をモデル化する．音響単極音源の例として，半径が拡張と収縮を繰り返す小さい球がある[16]．音媒体の体積は，単極音源の強さとして知られる割合 で単極音源によって取って代わられる．

単極音源を利用するために，単極音源を に置く．単極音源項 は以下のように書かれることがある：

ここで は音源位置 におけるディラック(Dirac)のデルタ関数である．

しかしディラックのデルタ関数は離散化された空間領域で解くことができないため，数値的なシミュレーションでは問題がある．これはディラックのデルタ関数が音源位置 で特異であるためである．したがって，ディラックのデルタ関数の近似が必要となる．ディラックのデルタ関数の近似処理のことを正規化という．

デルタ関数 を正規化する方法はいろいろある[17,18]．このチュートリアルでは次の方法を使う．

ここで は，正規化されたデルタ関数 のサポートを制御する正規化パラメータである．通常 はメッシュ間隔 に相当するサイズを持たなければならない．

を変更すると正規化デルタ関数の幅が変化するが，では空間積分は常に1である．

次に波動方程式(19)を使って1Dの時間非調和波モデルを構築し，NDSolveValueを使って数値的に解く．

このアニメーションの振幅は，どの正規化デルタ関数 を選ぶかに依存し，単極音源の強さ と混同しないようにしなければならない．

単極音源の解析音圧振幅は[20]で与えられる．

結果の波には正弦波時間依存性があり，単極音源は音を等方的に放射する における点源であることが分かる．

二重極音源は，強さが等しいが反対の位相であり距離 だけ離れた2つの単極音源からなる．この分離距離は，音源の波長と比較すると小さい．1つの単極音源とは異なり，二重極音源による体積変異はない．2つのうちの1つとして，二重極は2番目の収縮を拡張する．単極音源と二重極音源のさらなる違いとして，二重極音源は音を等方的に放射しないとうものがある．

二重極音源が2つの単極音源の組合せであることを示すために，において距離 だけ離れた2つの単極音源から作成された二重極音源をモデル化する．(21)で選んだ正規化デルタ関数 に基づいて，分離距離は自動的に と設定される．

この場合，正規化パラメータ は，2つの単極音源が重ならないように小さくなければならない．重なった単極音源では二重極音源が正しくモデル化されないからである．

2つの単極音源は のとき重なり始める．対応する重ね合せ（青線）はもはや積分規則を満足せず，正しく二重極音源をモデル化することができない．

波動方程式(22)の単極音源項 は2つの単極音源の和になる：．

アニメーションの振幅は，どの正規化デルタ関数 を選んだかによって異なり，単極音源の強さ と混同してはならない．

二重極音源の解析音圧振幅は[23]で与えられる．

二重極音源は音を等方的に放射しない．結果の音波は正弦波であるが反対の位相である．

波動方程式 において，二重極音源 は先に例示した2つの単極音源と等価である．波動方程式(24)の二重極音源 は(25)と書くことができる．ここで は二重極音源の強さを表す：

二重極音源の強さ は単極音源ペアの強さ ，媒体密度 ，分離距離 の積に等しい．

単極音源の場合と同様に，ディラックのデルタ関数は正規化されなければならない．前に定義した は連続的な一次導関数を持つので，波動方程式(26)の発散項に現れる二重極音源 をモデル化するために使うこともできる．

アニメーションの振幅は正規化デルタ関数 の選択に依存するため，二重極音源の強さ と混同してはならない．

結果の音場は等方的ではないが，2つの単極音源を繋ぐ軸について対称である．

解析的には，二重極音源 は対応する音源の強さを持つ一対の単極音源に等しい．しかし，離散化された領域で本当のデルタ関数を近似するために正規化デルタ関数 を適用したため，単独の二重極音源と1対の単極音源から作成されたモデルの間に差がある．この差は正規化デルタ関数 のサポート内にのみ存在する．

予想通り，二重極モデルは正規化デルタ関数()の外側では1対の単極モデルに合致している．つまり，二重極は1対の単極音源 を組み合せたものであり，二重極音源項 により直接モデル化できるということである．

一階方程式系としての波動方程式

次のセクションでは音の伝搬をモデル化する別の方法を紹介する．これには一階微分方程式系を使う．完全整合層 (PML) が使われる場合等，場合によっては一階微分方程式系を使うことが音響系を解く唯一の方法である．一階偏微分方程式の再定式化を使うことで，解く過程における時間とメモリの効率をよくすることもある．

縦波によって媒体を介して音が伝達されると仮定する．これは粒子が伝搬の方向に前後に動くことを意味する．これらの粒子の運動は粒子変位 として表され，その時間微分は粒子速度 を与える：

粒子速度 は音速 とは異なる．後者は縦波が伝搬する速度である．

質量保存と運動量保存の方程式はそれぞれニュートンの法則と理想気体の法則[27]によって定式化することができる．

一階連立波動方程式は(28)と(29)の組合せである．

例として，時間調和波の1Dモデルを考える．

一階連立波動方程式でモデルを構築するときは，粒子速度 に対する追加の初期条件と境界条件が必要である．

追加の初期条件と境界条件を設定するためには，まず固有音響インピーダンス を定義しなければならない．固有音響インピーダンスは，波が媒体の中を移動するときの粒子速度に対する音圧の割合を表す．これは下のように書くことができる．

平面波の場合，固有音響インピーダンスは媒体の密度と音速[30]の積に等しいことを示すことができる．インピーダンスについては「インピーダンス境界条件」というセクションで詳述している．

(31)を使って特定のインピーダンスを持つ追加の境界条件を定式化することができる：

この場合，初期条件はゼロに設定されている．正弦波の音圧源が領域の左端に置かれるよう，境界条件を強制する．

一階連立方程式が対流支配であることを示すメッセージが生成されている．(32)および(33)の空間微分項すべてが一次のみで音波の移流輸送（または対流輸送）[34]を表しているので，このメッセージが生成されることは想定内である．

この問題についての詳細は有限要素法の使い方のヒントについてのチュートリアルに記載されている．

この結果を、二階波動方程式(35)で計算した別の結果と比較するのは有益である．

一階PDE系を使うと，誤差，メモリの使用量，時間が大きく減少する．これは大規模な音響モデルを解く際に非常に便利である．

連立一階方程式としてモデル化された2Dバージョンの波動方程式については，これをご参照いただきたい．そこで提示されている例題は完全整合層(PML)を使っているので，支配方程式(36)で2つの追加の因子 および （完全整合層の吸収係数）が導入される．一旦 と がゼロに設定されると，方程式(37)はPML範囲外部のシミュレーション領域で連立の一次波動方程式(38)， (39)に描画される．

損失媒体における音の伝搬

多孔質材等の損失媒体における音の伝搬をモデル化するためには，音波[40]の減衰を受け入れるよう，波動方程式(41)を変更する必要がある．有効体積弾性率 および についての一階時間微分が左辺に加えられる．

減衰項と有効体積弾性率 は，断熱圧縮率からの偏差とともに多孔性，流れ抵抗の効果の主原因となる．多孔性 は媒体の全体積 に対する空の空間 の比率として定義され，流れ抵抗 は粒子速度 に対する音圧勾配 の比率として定義される．一般的な音吸収質材の場合， はから の範囲内にある．

損失媒体において， は音の消失によって断熱体積弾性率 から逸れる場合がある． の値は周波数 と流れ抵抗 とともに変化し，DelanyとBazleyandの実験式[42]によって近似することができる．，，のとき，方程式(43)は無損失の波動方程式(44)に簡約される．

有効体積弾性率 は特定の周波数 に依存するので，損失媒体モデル(45)は単独の周波数波，つまり時間調和波だけのシミュレーションに制約される．複数の周波数からなる時間非調和波をモデル化するためには，解析の前に波をフーリエ変換で分解しておく必要がある．

例として，周波数 における調和音波を考える．これは多孔質吸音材で満たされた管を通って伝搬する．この材質の多孔性と流れ抵抗はそれぞれ と で与えられる．

波の反射を避けるために，右側に吸収境界条件を加える．修正された波動方程式(46)を受け入れるために，NeumannValueを に設定する[47]．

損失媒体では，音波は領域内で減衰する一方で低速度で伝搬する．

音響的境界条件

音響学でもっとも一般的な境界条件はDirichletConditionおよびNeumannValueでモデル化でき，次の4つに分類することができる．

• ディリクレタイプの境界条件．このタイプの境界条件は境界における音圧 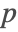を指定し，DirichletConditionでモデル化することができる．

• ノイマンタイプの境界条件．このタイプの境界条件は境界における粒子速度 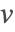を指定し，NeumannValueでモデル化することができる．

• ロビンタイプの境界条件．このタイプの境界条件は境界における時間と音圧の法線導関数の関係を指定し，NeumannValueでモデル化することができる．ロビンタイプの境界条件は技術的に言えば一般化されたノイマン境界条件だからである．

• 周期境界条件．このタイプの境界条件は境界の一部の音圧 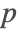を別の部分にマップし，PeriodicBoundaryConditionでモデル化することができる．

この4つのタイプのもとで，次のような境界条件が導入される．

• ロビンタイプ

• インピーダンス境界条件

• 吸収境界条件

• 放射境界条件

• ノイマンタイプ

• Sound Hard境界条件 - 壁

• 法線速度境界条件

• 圧力源境界条件（ノイマンモデル）

• ディリクレタイプ

• Sound Soft境界条件

• 圧力源境界条件（ディリクレモデル）

• 周期タイプ

• 周期境界条件

次のセクションでは音響でよく使われる物理的境界のいくつかを説明し，DirichletCondition，NeumannValue，PeriodicBoundaryConditionを使ってモデル化する方法を示す．このため，現在議論されている境界条件は常にシミュレーション領域の右側にある．例題によっては，右側の境界条件の挙動をよりよく例示するために，左側に追加の境界条件がある場合がある．

一般にソルバアルゴリズムでは， が成り立つような境界 上の流束を指定するためにNeumannValue[g-q p(t,X) ,X∈Γ_b]を使う．

しかし音響モデルでは，二重極源 は領域内でしか指定できず，境界のどの部分上でも常にゼロに等しいため となる．

インピーダンス境界条件

境界上でインピーダンスが指定されている場合，インピーダンス境界条件は以下で与えられる：

音波が一つの媒体から別の媒体に伝搬するとき，音波の一部がその接触面で反射したり接触面全体に伝わったりする．次の例では，この挙動を示すために2つの音響媒体で満たされた管を考える．

軸に沿い，音波長 よりずっと小さい直径 を持つ管の場合，, 平面の点はすべて同じ音圧値 および同じ粒子速度 を持つと想定するのが妥当である．この波のタイプは平面波と呼ばれ，一次元の波として扱うことができる．

インピーダンス境界条件をよりよく説明するために，この例では標準偏差 のガウスパルスを使う．

この領域は で2つの媒体に別れる．左の媒体は冷気であり，右の媒体は暖気である．

この例ではシミュレーション領域がわずかに拡大されている．こうすることで，シミュレーション時間が終了するまで波が右の境界に到達しない．

この音圧場のアニメーションは音波が左から右に移動していること，および2つの媒体が .において中央に接触面を形成していることを示している．接触面では波は同じ速度で反射されるが極性は逆になる．波の残りの部分はより高速に接触面を伝わるが振幅は小さい．波の振幅は両方の領域の材料特性に依存する．反射波はややsound soft境界のように動作する．これは密度の差が であるために起こる． となるように密度を変更すると，異なる反射になる．これは , を , に変更するだけでチェックすることができる．

この入射波，反射波，伝達波の間の関係を定式化するために使われる特性は，固有音響インピーダンスと呼ばれることがある．固有音響インピーダンス は音波が媒体を移動するときの音の粒子速度に対する音圧の比であり，以下で定義される：

平面波の場合，固有音響インピーダンスは媒体の密度と音速[48]の積に等しいことを示すことができる：

1つの媒体から別の媒体に伝搬する音波では，振幅関係は固有音響インピーダンス で以下のように表すことができる：

ここで ，， はそれぞれ反射波，入射波，伝達波の振幅である．とはそれぞれ媒体1と2の固有音響インピーダンスである[49]．

これらのパラメータを使って解を検証することができる．

たとえば媒体の解に関心がない場合は，解にその領域を含む必要はない．媒体の接触面は における境界の媒体のインピーダンスを指定することによってモデル化することができる．これはインピーダンス境界条件と呼ばれる．インピーダンス境界条件はロビン境界条件としても知られている一般化ノイマン境界条件で実現することができる．

インピーダンスの定義(50)を運動量保存方程式(51) に代入することで，インピーダンス境界条件は境界インピーダンス を使って以下のように表すことができる：

既知の境界インピーダンス を持つ例を再構築するため，NeumannValueを に設定する．の定数はNeumannValueの指定 に合致する必要があるという点に注意する．ここで と は0， は に合致するため，使用する波動方程式(52)と整合している．また，媒体境界は右側()にある．NeumannValueの時間微分の意味は「時間微分のノイマン値」のセクションで詳しく説明する．

このアニメーションはシミュレーション領域が小さいこと以外，前の例と同じ結果を示している．

原理上はインピーダンス境界条件を使うと両方の媒体で方程式を解く必要がなくなるので，シミュレーションの過程がより効率的になる．

概念上は，インピーダンス境界条件は3つのタイプの境界条件の一般化である．

• 両方の媒体が同じ場合，方程式に を挿入し，吸収境界条件を得る．

• 境界のインピーダンスが無限に近付く場合，方程式に 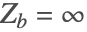を挿入し，sound hard境界条件を得る．

• 境界のインピーダンスがゼロに近付く場合，(53)の両辺に を掛け，が0に近付くときの極限を取る．得られる方程式は 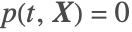であるsound soft境界条件の定義に一致する．sound soft境界条件はDirichletConditionで直接モデル化しなければならない．

吸収境界条件

特定のタイプの入射波および波源から境界までの距離 がある場合、吸収境界条件は以下で与えられる：

• 平面波：

• 円筒波：

• 球面波：

通常，無限にまで拡張されるシミュレーション領域は，シミュレーションにおいて実現可能なオプションとは言えない．吸収境界条件は無限での境界をモデル化するのに使われる方法である．吸収境界条件(ABC)は到来波を吸収することで動作するため，モデルが無限範囲を持つかのように動作させる．シミュレーションを無限範囲でモデル化する方法は吸収境界条件だけではない．吸収境界条件の代りに完全整合層を使うこともできる．　　　　　　　　　　　　

吸収境界は計算領域の続きなので，境界インピーダンスはその領域の固有音響インピーダンスに等しい．つまり吸収境界条件はNeumannValue内の従属変数の時間微分を利用するインピーダンス境界条件の特殊な場合なのである．NeumannValueにおける時間微分の意味は時間微分のノイマン値で詳しく説明する．

平面波の場合，固有音響インピーダンスは であることを思い出してほしい． をインピーダンス境界条件(54)に代入すると吸収境界条件は以下のように書くことができる：

さまざまな種類の波に対応するために，方程式(55)は追加の項 を使って一般化することができる[56]：

平面波では ，円筒波では ，球面波では が使われる．

ここで は波源から吸収境界までの距離である．

例として，計算領域が から に設定された無限長の管を見る．領域の続きをモデル化するために，右端に吸収境界条件を加える．

到来波は，シミュレーション領域が無限範囲を持つかのように，右側の境界で収集される

よい吸収境界条件の質的な特徴として，シミュレーション領域に反射される到来波の量がある．理想的には何も反射されないのがよい

．

数値誤差は有限要素法の離散化によるものである．誤差は波が右側に到達しても増加しない．つまり，1Dの場合は吸収境界ではほとんどあるいは全く反射しない．

しかし，吸収境界条件は厳密に直角入射でのみ波を吸収することができる．波が任意の角度で境界にぶつかる2Dや3Dの場合，吸収境界で数値的反射が起こる．これは吸収境界を持つ2D領域における円筒波の伝搬のシミュレーションで説明する．

アニメーションの質を向上させる方法はこちらでご覧いただきたい．

入射角が境界に垂直ではない4つの角における反射波に注目のこと．幾何学的に異なると，反射は幾分小さくなる可能性がある．

2Dや3Dで波の反射を減少させるためには，吸収境界をモデル化する別の方法として，PMLを適用することができる．PMLは，非正規に境界にインパクトを与える波がその内部で吸収されるよう設計されている．PMLについては完全整合層(PML)で詳しく説明する．

Sound Hard境界条件（壁）

壁境界の場合，sound hard境界条件は以下で与えられる：

境界上の音の粒子速度は機械振動の速度に対応する．sound hard境界では，境界の粒子変位はゼロ に固定される．その結果，境界に垂直な粒子速度の要素もゼロになる．

sound hard境界では，音の速度が なのでインピーダンス は無限に近付く．つまり，sound hard境界条件はインピーダンス境界条件の特殊な場合なのである．

ニュートンの法則[57]から導出された運動量保存方程式(58)は，音圧 と音の粒子速度 を関連付ける：

(59)と(60)を組み合せると，sound hard境界条件は境界に垂直な方向における音圧の偏導関数がゼロであることも暗示していることが分かる：

例として一方の端が閉じた管を見てみる．

境界のどの部分でも境界条件が指定されていない場合，デフォルトではノイマンのゼロ境界条件が使われる．これは，指定された境界において境界条件が指定されていない場合は，sound hard境界がデフォルトの境界条件として使われることを意味する．

この音圧場のアニメーションは音波がsound hard境界に向かって左から右に移動していることを示している．概念上，sound hard境界は管の閉じた端と同じである．前進運動は不可能なので，音圧は蓄積し，入射圧力の倍で最大値に達する．その後圧力波は逆方向に動き始める．波は入射波と同じ速度，振幅，両極性で反射されることに注意する．

法線速度境界条件

境界 上で音の粒子速度が と指定されている場合，法線速度境界条件は以下で与えられる：

境界に垂直な音の粒子が指定されておりそれがゼロではない境界は法線速度境界と呼ばれる．法線速度境界の身近な例として，音波を周囲の媒体に生成する振動する機械構造がある．

音の粒子速度が外側の法線 と反対に指定されていることを示すために，の前に負の符号を加える．こうすることで，音圧が常に境界上の粒子速度と同相であることが確実にできる．

運動量保存方程式(61)が音圧 と音の粒子速度 を関連付けるということを思い出してみよう．

(62)を(63)代入すると，法線速度境界条件は以下のように書くことができる：

次の例では，右側の境界に振動が導入され，既知の速度 で振動する．音場は以下に示すようにNeumannValueを使って計算することができる．

シミュレーションは初期条件で始まり，法線速度境界条件は左に伝搬する正弦波を右の境界で生成する．波の前の僅かな揺らぎは，空間離散化による中間生成物である．この効果はAcousticOptionsでメッシュの解像度を高くすることで減少させることができる．

このアニメーションは圧力源境界条件で示した例とよく似ている．それは，音圧 と粒子速度 が互いに で与えられる線形依存性を持つからである．ここで は固有音響インピーダンスなので，音圧の摂動が音の粒子速度の摂動も引き起こす．固有音響インピーダンスが既知の場合，法線速度境界は圧力場境界で置換することができる．

Sound Soft境界条件

sound soft境界条件は以下で与えられる：

sound soft境界では，境界の媒体圧力は で表される周囲の基準圧力に等しく設定される．音の粒子が境界で自由に動けるため，このタイプの境界はsound free境界とも呼ばれる．これは音の粒子速度がゼロであることが要求されないことを意味する．運動量保存方程式 は音の粒子変位 と音圧 に関連する．である間， は必ずしもゼロに等しくはない．

sound soft境界では音圧 であるためインピーダンスである．つまり，境界インピーダンスがゼロに設定されているとき，sound soft境界条件はインピーダンス境界条件の特殊な形なのである．

この動作を例示するために，次の例では一端が開いた管を考える．開いた端は音の粒子の動きについての制約条件を持たないため，sound soft境界として扱う．

音圧場のアニメーションは音波が左から右に移動するのを示している．右端にはsound soft境界がある．概念上はsound soft境界は管の開いた端と等価である．波が開いた端に到達すると，その圧力は周囲の圧力にまで引き下げられる．これにより吸引力が発生し，負の圧力パルスが形成され，その負の圧力パルスは反射波として逆向きに動き始める．波は入射波と同じ速度および振幅で反射されるが位相角度は変化する．

圧力源境界条件

境界上で音圧 が指定されている場合，圧力源境界条件は以下で与えられる：

境界で非零の時間依存の音圧が指定されると，圧力源境界条件を考える．圧力源境界条件はDirichletConditionおよびNeumannValueを使って指定することができる．

例えば時間依存の正弦圧波を生成する振動パネルをモデル化するためには，圧力源は右端で時間依存の正弦圧力 として設定することができる．波の反射を避けるために，左端に吸収境界条件を加える．

このシミュレーションは平静な領域から始まり，過渡圧力振動が右側の境界で正弦波を生成しそれが左に伝搬する．

単極源が波を等方的に放射する一方で，圧力源は境界に垂直な波を生成する．したがって1Dの場合，境界の圧力源はDirichletConditionを波動方程式(64)の右辺の等価の単極源で置換することによってモデル化することができる．単極源については単極源で詳しく説明する．

圧力源はNeumannValueでモデル化することもできる．これを行うと，境界の同じ部分において圧力場は他のノイマン値ベースの境界条件モデルと組み合せることができるという利点がある．つまり境界の同じ部分でいくつかのノイマン値を組み合せることによって，ハイブリッドの境界条件が作成できるのである．このようにすることで，たとえば，圧力源を吸収境界と組み合せて放射境界条件を形成することができる．

圧力場に対するNeumannValue設定は法線速度境界条件から導出することができる．

平面波では固有音響インピーダンス であることを思い出してほしい．を(65)に代入すると，この方程式は指定された音圧 で以下のように表すことができる：

例として，NeumannValue設定(66)で時間依存の圧力源 をモデル化する．

ディリクレ条件は境界ノードで特定の値を強制するため，ディリクレモデルの方が正確である．つまり，ノイマン値を含む圧力源のモデリングは，その圧力源と別のノイマン値ベースの境界条件を組み合せる必要があるときに行われる．

放射境界条件

境界上に入射音圧 と波の方向ベクトル が指定されている場合，放射境界条件は以下で与えられる：

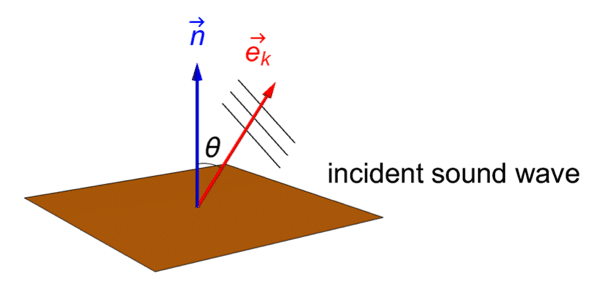
境界法線ベクトル ，波の方向ベクトル ，波の入射角 の関係は以下に示す通りである：

したがって，方程式(67)も波の入射角 で次のように表すことができる：

1D領域で放射境界を適用する場合，入射角 は常にゼロ（垂直入射）である．よって，方程式(68)は下のように簡約できる：

1Dの放射境界の例は次のセクションで示す．斜入射の放射音波を示す2Dの例は，付録のセクション斜入射の放射音波に挙げてある．

このセクションでは，1D領域の放射境界条件を導出する．2Dおよび3Dでの完全な導出については， GivoliとNetawe[69]の研究をご参照いただきたい．

概念上は，放射境界は圧力源境界と吸収境界の特性を組み合せたハイブリッドの境界条件である．入力波を生成するために非零の時間依存の音圧 が境界で指定されるが，単純な圧力源とは異なり，放射境界では出力波はほとんど反射なしで計算領域を出ることができる．

放射境界条件を導出するために，音圧場は入力波 と出力波 に分解され，以下のようになる：

入力波 を生成する一つの方法として，境界において指定された音圧 を持つ圧力源境界条件を使うというものがある．

出力波 が制約条件なしで境界を離れることを確かにするために吸収境界条件を適用する．

方程式(70)と(71)を足して(72)を挿入すると以下になる：

境界上では入力波の振幅は によって指定されるということを思い出してほしい．この関係を(73)の右辺に代入すると，次の放射境界条件になる：

この動作を示すために，次の例で一端が閉じた半無限の管を考える．右端から調和音波が計算領域に入る．波は管を通過する．左端はsound hard境界として扱われる．波が右端に戻ってくると，これは吸収される．圧力源になり反射波を吸収するこの過程が放射境界条件である．

このアニメーションは放射境界によって生成される左移動の波を示す．この波は左端で反射され入射波と重なる．反射波が放射境界を離れ始めるにつれ，音圧場はその動的安定状態に達する．結果の波は右にも左にも動かず，単に正しいテンポで振動する．

このタイプの波は定常波と呼ばれる．これについては「周波数領域における音響学」で詳しく説明する．

周期境界条件

音圧 を音源境界から周期境界にマップする関数 がある場合，周期境界条件は以下のように書ける：

周期境界条件は空間的に周期的な領域における音波をモデル化するために使われる．つまり，一つの境界（ソース境界といわれる）から得られた情報を関連関数 を使って別の境界（周期境界といわれる）にマップすることができるのである．周期境界条件は音響PDEモデルのPeriodicBoundaryConditionで設定される．

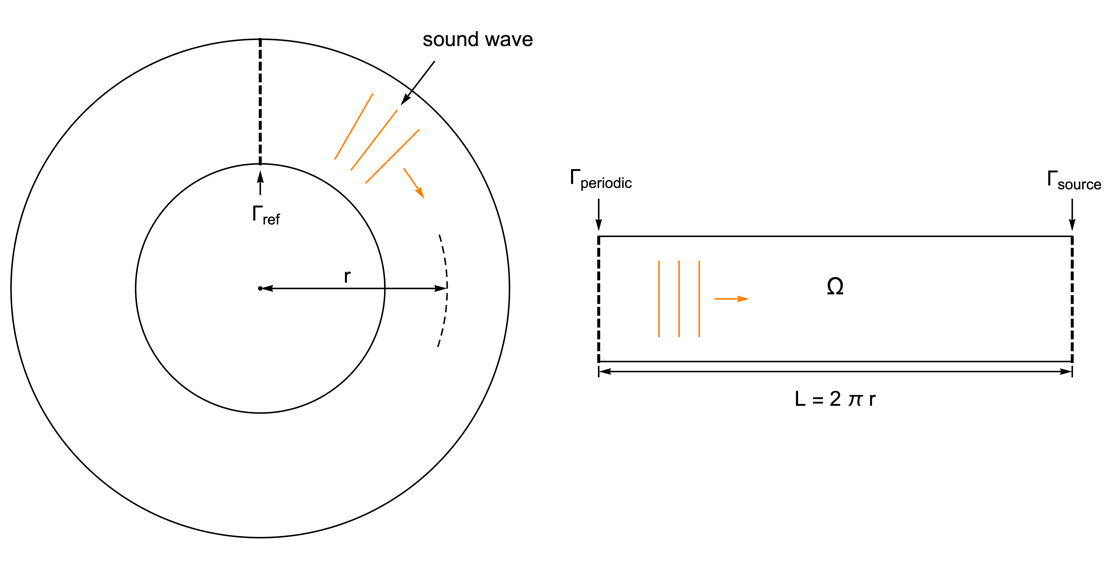
例として，円管で伝播する音波を見る．周期境界条件を使うことで，1D領域でシミュレーションを行うことができる．

円管は，管の円周に等しい長さ の1Dモデルに変換される．音波が領域の右側を通過するとき，それが同じ大きさで左側にも現れるように，周期境界は左端に設定される．

この例では初期音波が誤差関数Erfで設定されている．初期条件の導関数はゼロではなく，初期波が右に移動するよう選ばれる．

波の反射を避けるために，右端に吸収境界条件を加える．

アニメーションは，空間的に周期的な領域内で右に移動する音波を示している．音波が右の境界を通過するときに，周期境界条件で設定された領域の周期性により，左端に再び現れる．音の媒体は音響的に無損失であることが想定されるため，波の大きさは常に一定レベルに保たれる．

完全整合層 (PML)

完全整合層(PML)は無限範囲のシミュレーション領域をモデル化する方法である．したがって，PMLは吸収境界条件の代替方法と言える．しかしPMLは境界条件ではなく，もとのシミュレーショングリッドを拡大する人為的な追加の吸収層である．波が吸収層に入ると，吸収によって減衰し指数関数的に崩壊する[74]．PMLが通常の吸収境界条件とは異なる主な特性は，前者は波が非PML領域からPMLに伝搬し，どの入射角における接触面でも反射しないよう設計されているという点である．つまり，PMLは非反射の吸収材のように動作するのである．PMLの詳細付録セクションの完全整合層の導出でご覧いただきたい．

PMLを実装するためには，2つのことが必要になる．まずシミュレーション領域が拡張されなければならない．この拡張はPMLがアクティブとなる領域である．次に，PDEの座標変換が行われる．

波動方程式は一階のみの空間微分を含む連立微分方程式に分けた方がよい．その後，もとの波動方程式の1回の変換(75)によってPML生成のすべてのプロセスを実行することができる．

PMLの座標変換後の連立一階波動方程式は以下である．

吸収係数は選択しなければならないパラメータであり，PML内でから に線形に増加するよう設定される．薄いPMLにはより大きいの値が要求されるが，大きいは数値的な反射を増加させる傾向がある．

PML接触面は，厳密で連続の波動方程式を解く場合に限って無反射である．しかしNDSolveはシミュレーション領域を離散化し，代りに波動方程式の近似を解く数値解法である．反射の量を減らすためには，より細かい格子，あるいはより小さい減衰率（より小さい）を使う必要がある．

ここでは例として，右にからまでのPMLを持つ，からまでの範囲の計算領域を使って，から までの1D領域のシミュレーションを考える．

音の媒体として空気を取る．一次元平面波の場合の固有音響インピーダンスは である[76]．

初期条件はゼロに設定される．境界条件は，正弦波圧力源が領域の左端に置かれるよう強制される．音の粒子速度 は によって音圧に関連付けられている．連立一階波動方程式としての設定の詳細は一階方程式系としての波動方程式をご覧いただきたい．

グラフから分かるように，もとの非PML領域では である．

連立一階波動方程式が対流支配であることを示すメッセージが生成されている．(77)の空間微分項すべてが一次のみで音波の移流輸送（または対流輸送）[78] を表しているので，このメッセージが生成されることは想定内である．このメッセージはOff[NDSolveValue::femcscd]を評価するとオフにすることができる．

この問題についての詳細は有限要素法の使い方のヒントについてのチュートリアルに記載されている．

薄いPMLでは，同じ減衰を得るためにの値が大きくなければならない．の値が大きくなると，通常数値的な反射が大きくなる．PMLの幅と減衰率の間のトレードオフを調べるために，このPMLモデルを次のように異なるパラメータで解く．

が小さい場合は波を減衰させるために幅の広いPMLが必要であるが，が大きい場合は数値的反射がより顕著である．

PMLの主な利点は入射波を等方的に吸収するというものである．これを示すために，四方にPMLを持つ2Dの単位正方形の例を考える．2D領域のシミュレーションは，とにおいてPMLを持つ計算領域を使ったである．

2Dの波動方程式にPMLを実装するために，2つの補助場変数およびを導入する[79]．方程式は次のようになる．

ここで と は空間の粒子速度要素である．

アニメーションの質を向上させる方法についてはこちらをご覧いただきたい．

吸収境界条件で示した以前の2Dの場合と比較すると，余分な時間とメモリ使用量を犠牲にして波はPMLのある角でよりよく吸収されるようになった．

付録

完全整合層の導出

完全整合層(PML)はグリッドの端に隣接して置かれる人工的な吸収層である．波が吸収層に入ると，吸収によって減衰し，指数関数的に崩壊する[80]．PMLが通常の吸収材質と異なる主な特性は，これは非PML媒体からPMLに伝搬する波が接触面で反射しないように設計されているという点である．つまりPMLは非反射吸収材のように動作する．

既述の通り，正のx方向に移動する時間調和波は以下のように表せる：

PMLの概念は，波動式(81)のすべての 項は複素変数 で置換される座標変換である：

ここでもとの は の実部としての役割を果たし， は吸収層における人工の虚部である．

このようにすることで，波はPMLにおいて指数関数的に崩壊するが，それ以外では変化しないままである．PMLの減衰率は人工的な虚部 の勾配によって制御される．薄いPMLの場合は大きい減衰率が必要である．つまり，大きい 値が割り当てられなければならない．しかし非常に大きい 値を使うとPMLの数値反射を増加させる可能性があるため，PMLの幅とその関連付けられた質とシミュレーション速度の間にはトレードオフがある．

ここで例として，右にからまでのPMLを持つ，からまでの範囲の計算領域を使って，から までの1D領域のシミュレーションを考える．これを行うためにPMLに勾配 の線形生育する虚部 を加える．

PML座標変換(82)により，波動式(83)は以下のように変換される：

新しい波動式(84)には余分な項 があるので，正の波の数 を持つ波は であるとき吸収層で指数関数的に崩壊する．

であるPML()の外側では波は変化しない．

これで波は急速に減衰し，になる前にほぼゼロまで崩壊する．換言すると，大きい減衰率（大きい 値）を使うと薄いPMLが使えるということである．

PML接触面()では反射がないため，非反射吸収材のように動作する．

PMLを実装するためには2つのことが必要である．まずシミュレーション領域が拡大されなければならない．この拡張はPMLがアクティブとなる領域である．次に，PDEの座標変換が行われる．座標変換では，波動方程式(85)のすべての 項が以下で定義される複素数値変数 で置換される．

PML減衰率を波周波数 [86]に独立にするためには，勾配 を以下のように設定する必要がある：

ここではユーザによって定義される吸収係数である．離散化された領域における数値的反射を最小化するために，はからのPML層内で線形に増加するよう設定する．座標変換は

あるいは，次のようになる．

しかし，もとの波動方程式(87)には二階空間微分が含まれている．したがって波動方程式を一階空間微分だけを含む連立微分方程式に分割した方が便利である．それからPMLの全プロセスはもとの波動方程式の1回の変換(88)によって実行することができる．

連立一次波動方程式は以下のように示すことができる．

したがって，1Dの場合は連立波動方程式は次のようになる：

調和波関係 および を適用する．方程式は次のようになる：

両辺にを掛けると次が得られる：

再び調和波関係を適用して，方程式を時間領域形式に戻す．最終的にPMLを持つ連立一階波動方程式は次のようになる：

時間微分のノイマン値

吸収境界条件は時間微分のNeumannValueでモデル化することができる．これは簡約された波動方程式を見ることでよく理解することができる：

(89)は方程式系として書くことができる．実際この変換はNDSolveで内部的に行われる．変換のために，次の補助方程式を導入する：

ここで(90)を(91)に代入して(92)を使うと，もとの波動方程式(93)の一階方程式と同等の系が得られる：

次に(94)からの代入を実行し，初期条件を変更する．

重要な点は，(95)を補助従属変数に適用することによって，ノイマン値の時間微分がどのように変わったかということである．この場合，ノイマン値の時間微分 は補助変数のノイマン値 によって置換される．

斜入射の放射音波

任意の入射角 の放射音波をモデル化するために，放射境界条件の一般方程式を使うことができる．

ここで は境界の入射音圧を表す．

例として，次の2Dの例を見てみる．時間調和音波は入射角 の底部境界から放射している．その後波は領域を通過し，上部境界から抜ける．

不規則的な図形の場合，境界条件の指定に要素マーカーを使うと便利である．メッシュにおけるマーカーとその生成についての情報は「要素メッシュ生成：マーカー」チュートリアルに記載されている．

アニメーションの質を向上させる方法についてはこちらをご覧いただきたい．

アニメーションから非正規の音波が において底部境界から放射されているのが分かる．その後音波は領域を通過して上部境界から出る．

用語集

次の表はこのチュートリアルで使われている記号名およびその意味を要約したものである．

    

記号	解説	単位
ρ	媒体の密度	[kg/m3]
c	媒体内の音速	[m/s]
p	音圧	[Pa]
pmax	音圧の最大値	[Pa]
	音圧振幅関数	[Pa]
	指定された境界圧力	[Pa]
t	時間	[s]
tend	シミュレーション終了時間	[s]
X	位置ベクトル	[m]
s	方向変換	N/A
F	オプショナルの二重極源	[N/m3]
	二重極源の強さ	[N/m3]
Q	オプショナルの単極源	[1/s2]
	単極源の強さ	[1/s2]
d	二重極源の分離距離	[m]
λ	音の波長	[m]
Ω	シミュレーション領域	[m]
k	波の数	[rad/m]
f	音波の周波数	[Hz]
ω	音波の角振動	[rad/s]
δ	ディラックのデルタ関数	N/A
	正規化デルタ関数	N/A
γ	正規化パラメータ	[m]
h	メッシュ間隔	[m]
Xs	音源の位置	[m]
α	減衰因数	[m2/(s·N)]
ϕ	多孔性	N/A
VV	空隙容量	[m3]
VT	合計容量	[m3]
Rf	流れ抵抗	[kg/(m3·s)]
β	ガウスパルスの標準偏差	[m]
ζ	音の粒子変位	[m]
v	音の粒子速度	[m/s]
	指定された境界速度	[m/s]
T	温度	[K]
Z	音響インピーダンス	[Pa·s/m]
Zb	境界インピーダンス	[Pa·s/m]
Ar	反射波の振幅	[Pa]
Ai	入射波の振幅	[Pa]
At	伝達波の振幅	[Pa]
	PMLの複素空間変数	[m]
fp	PMLのモデルパラメータ	[m]
mf	PMLの人工的虚部の勾配	N/A
σ	PMLの吸収係数	[rad/(s·m)]
σmax	吸収係数の最大値	[rad/(s·m)]
ψ	任意関数	N/A

参考文献

1.  Nolte, Bodo and Marburg, Steffen. Computational acoustics of noise propagation in fluids : finite and boundary element methods. Springer - Verlag, 2008.

2.  Heutschi, Kurt. Lecture Notes on Acoustics I. Swiss Federal Institute of Technology Zurich, 2016.

3.  Russell, Daniel. Acoustics and Vibration Animations: Reflections from Impedance and the Standing Wave Ratio, The Pennsylvania State University, 2013, www.acs.psu.edu/drussell/Demos/SWR/SWR.html.

4.  Saksela, Kai. Finite element analysis of 2D acoustics. Kai’s thoughts, 2013, blog.kaistale.com/?p=574.

5.  Fahy, Frank. Foundations of Engineering Acoustics. Academic Press, 2001.

6.  Johnson, Steven. Notes on Perfectly Matched Layers (PMLs). MIT, 2010.

7.  Bilbao, Stefan and Hamilton, Brian. Directional Source Modeling In Wave-Based Room Acoustics Simulation. IEEE, 2017.

8.  Peskin, Charles. The Immersed Boundary Method. Cambridge University, 2002.

9.  Russell, Daniel, Titlow, Joseph and Bemmen, Ya-Juan. Acoustic monopoles, dipoles and quadropoles: An experiment revisited. American Journal of Physics 67, 660, 1999.

10.  Zeleny, Enrique. Acoustic Multipoles, Wolfram Demonstrations Project, 2013, http://demonstrations.wolfram.com/AcousticMultipoles/.

11.  Zeleny, Enrique. Longitudinal and Transverse Waves, Wolfram Demonstrations Project, http://demonstrations.wolfram.com/LongitudinalAndTransverseWaves/.

12.  Moore, Guy. Lecture Note: The Physics of Music - Reflection and Impedance, McGill University, 2006.

13.  MATTER Project. Full Width Half Maximum (FWHM), The University of Liverpool, Department of Physics, 2000.

14.  Ihlenburg, Frank. The Medium-Frequency Range in Computational Acoustics: Practical and Numerical Aspects. Journal of Computational Acoustics, Vol.11, No. 2 175-193, 2003.

15.  Vita, Micro. The Wave Equation with a Source. Oklahoma State University.

16.  Maderuelo-Sanz et al. Acoustical performance of porous absorber made from recycled rubber and polyurethane resin. Latin American Journal of Solids and Structures, Vol.10, No.3, 2013.

17.  Turkel, E. and Yefet, A. Absorbing PML boundary layers for wave-like equations. Applied Numerical Mathematics, 27(4) 533-557, 1998.

18.  T. Cox, P. D'Antonio. Acoustic Absorbers and Diffusers: Theory, Design and Application. Spon Press, 2004.

19.  B. Engquist and A. Majda. Absorbing Boundary Conditions for the Numerical Simulation of Waves. Mathematics of Computation, Vol. 31, No. 139 629-651, 1977.

20.  D. Duran. Numerical Methods for Fluid Dynamics - With Applications to Geophysics, second edition, Springer, 2010.

21.  D. Givoli and B. Neta. High-order Non-reflecting Boundary Scheme for Time-dependent Waves. Journal of Computational Physics, Vol. 186, 24–46, 2004.

関連するテクニカルノート

▪
• 時間領域における音響学
▪
• 周波数領域における音響学
▪
• 音響モデルコレクション
▪
• PDEModelsの概要