ThermodynamicData

ThermodynamicData["name","property"]

gives the value of the specific property for the substance "name".

ThermodynamicData["name","property",{parameter1quantity1,parameter2quantity}]

gives the value of the specific property for the substance "name" at the specified parameters.

Details

  • ThermodynamicData[] gives a list of the available substances.
  • ThermodynamicData["Properties"] gives a list of all properties available.
  • Properties that do not apply or are not known in a particular case are indicated by Missing[…].
  • Properties are returned using Quantity where appropriate.
  • If not otherwise specified, physical properties are given for standard temperature and pressure (293.15 K and 101325 pascals). If a single parameter is specified, that value will be coupled with standard temperature (or pressure if the parameter is "Temperature") to derive a value.
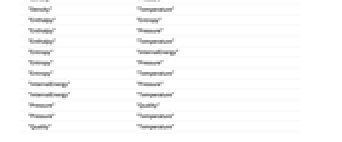
  • Parameters include "Density", "Enthalpy", "Entropy", "InternalEnergy", "Pressure", "Quality" and "Temperature".
  • Supported combinations of parameters include:
  • "Density""Enthalpy"
    "Density""Pressure"
    "Density""Temperature"
    "Enthalpy""Entropy"
    "Enthalpy""Pressure"
    "Enthalpy""Temperature"
    "Entropy""InternalEnergy"
    "Entropy""Pressure"
    "Entropy""Temperature"
    "InternalEnergy""Pressure"
    "InternalEnergy""Temperature"
    "Pressure""Quality"
    "Pressure""Temperature"
    "Quality""Temperature"
  • Parameter values can also be supplied as an Association.
  • ThermodynamicData["name"] returns all properties with their values at STP. ThermodynamicData["name",{parameter1quantity1,parameter2quantity}]returns all properties using the supplied parameters to calculate values.
  • The common English name for a supported substance can be found using the "property" "Name".
  • Parameter-dependent properties include:
  • "AdiabaticBulkModulus"bulk modulus for adiabatic compression
    "AdiabaticCompressibility"volume change at constant entropy
    "B12"mixed second virial coefficient
    "ChemicalPotentials"change in Gibbs free energy due to change in amount
    "CompressibilityFactor"correction factor from ideal gas behavior
    "Density"density
    "DerivativeOfPressureWithRespectToDensityAndTemperature"derivative of pressure with respect to density and temperature
    "DielectricConstant"ratio of permittivity to permittivity of vacuum
    "DynamicViscosity"dynamic viscosity
    "Enthalpy"enthalpy
    "Entropy"entropy
    "ExcessEnergy"difference between actual and ideal internal energy
    "ExcessEnthalpy"difference between actual and ideal enthalpy
    "ExcessEntropy"difference between actual and ideal entropy
    "ExcessGibbsFreeEnergy"difference between actual and ideal Gibbs free energy
    "ExcessHelmholtzFreeEnergy"difference between actual and ideal Helmholtz free energy
    "ExcessVolume"difference between actual and ideal volume
    "FirstDerivativeOfDensityWithRespectToPressure"derivative of density with respect to pressure
    "FirstDerivativeOfDensityWithRespectToTemperature"derivative of density with respect to temperature
    "FirstDerivativeOfPressureWithRespectToDensity"derivative of pressure with respect to density
    "FirstDerivativeOfPressureWithRespectToTemperature"derivative of pressure with respect to temperature
    "FourthVirialCoefficient"fourth virial coefficient
    "GibbsFreeEnergy"Gibbs free energy
    "HelmholtzFreeEnergy"Helmholtz free energy
    "InternalEnergy"internal energy
    "IsenthalpicJouleThomsonCoefficient"temperature change due to pressure at constant enthalpy
    "IsentropicExpansionCoefficient"heat capacity ratio
    "IsobaricHeatCapacity"heat capacity at constant pressure
    "IsochoricHeatCapacity"heat capacity at constant volume
    "IsothermalBulkModulus"bulk modulus at constant temperature
    "IsothermalCompressibility"volume change at constant temperature
    "IsothermalExpansionCoefficient"expansion due to pressure at constant temperature
    "IsothermalThrottlingCoefficient"isothermal throttling coefficient
    "MolarDensity"density per molar mass
    "MolarEnthalpy"enthalpy per molar mass
    "MolarEntropy"entropy per molar mass
    "MolarInternalEnergy"internal energy per molar mass
    "MolarIsobaricHeatCapacity"heat capacity at constant pressure per molar mass
    "MolarIsochoricHeatCapacity"heat capacity at constant volume per molar mass
    "MolarSpecificVolume"molar volume
    "Phase"phase
    "SecondAcousticVirialCoefficent"second viral coefficient of the adiabatic sound speed
    "SecondDerivativeOfPressureWithRespectToDensity"second derivative of pressure with respect to density
    "SecondDerivativeOfPressureWithRespectToTemperature"second derivative of pressure with respect to temperature
    "SecondVirialCoefficient"second virial coefficient
    "SoundSpeed"speed of sound
    "SpecificHeatInput"specific heat input
    "SpecificVolume"specific volume
    "ThermalConductivity"thermal conductivity
    "ThirdAcousticVirialCoefficent"third viral coefficient of the adiabatic sound speed
    "ThirdVirialCoefficient"third virial coefficient
    "VolumeExpansivity"volume expansion with temperature
  • "Enthalpy", "Entropy", and their molar forms are measured relative to their values at the boiling point of the substance.
  • "Phase" is unavailable for parameter combinations outside of "Temperature" and "Pressure".
  • Triple point properties include:
  • "TriplePointGasDensity"density of gas at the triple point
    "TriplePointLiquidDensity"density of liquid at the triple point
    "TriplePointPressure"pressure at the triple point
    "TriplePointSolidDensity"density of solid at the triple point
    "TriplePointTemperature"temperature at the triple point
  • Critical point properties include:
  • "CriticalDensity"density at the critical point
    "CriticalEnthalpy"enthalpy at the critical point
    "CriticalEntropy"entropy at the critical point
    "CriticalInternalEnergy"internal energy at the critical point
    "CriticalPressure"pressure at the critical point
    "CriticalTemperature"temperature at the critical point
  • Phase boundary properties include:
  • "SolidLiquidPhaseBoundary"given the temperature or pressure, returns the corresponding value on the solid-liquid phase boundary
    "SolidVaporPhaseBoundary"given the temperature or pressure, returns the corresponding value on the solid-vapor phase boundary
    "LiquidVaporPhaseBoundary"given the temperature or pressure, returns the corresponding value on the liquid-vapor phase boundary

Examples

open allclose all

Basic Examples  (5)

Find the entropy for water at standard pressure and temperature:

Calculate the speed of sound in ammonia:

Find the viscosity of air at a specified temperature and pressure:

Learn the densities of the phases of water at the triple point:

Find the temperature where liquid water has maximum density:

Scope  (8)

Names  (2)

Obtain a list of substance names:

Find the common English name for a substance:

Properties  (3)

A property value can be any valid Wolfram Language expression:

Obtain a list of properties:

The phase boundary properties return the missing thermodynamic coordinate:

Thermodynamic Parameters  (3)

Parameter specifications accept lists of quantities as inputs:

Use a range of thermodynamic parameters to compute properties of a substance:

Association can be used to supply thermodynamic parameters:

Applications  (9)

Plot entropy versus temperature for ammonia:

Explore the relationship between density and temperature for various substances:

Find the energy needed to heat cool water to steam in kilojoules:

Explore the phase diagram of a substance:

Construct the pressure versus entropy Mollier diagrams:

Determine the specific Gibbs and Helmholtz free energy for sulfur dioxide:

Find the volume curves for constant pressure and constant temperature:

Interpolate over those curves and find to get and :

Using the relation , derive the isobaric heat capacity:

Compare the calculation to the actual value:

Plot the Planck thermodynamic potential in three dimensions:

Assemble the values:

Examine the Stirling cycle for 10 moles of air:

Calculate the isothermal expansion and compression curves at 200 °C and 100 °C, respectively:

Create the diagram:

Calculate mechanical work through :

Find maximal and minimal pressures for expansion and compression:

Calculate change in internal energy:

Using work and the change in internal energy, calculate efficiency:

Compare with maximal possible Carnot efficiency:

Possible Issues  (6)

Using nonstandard substance and property names will not work:

Quantities should be dimensionally correct:

Only some combinations of parameters are supported:

Data for solids is not available from this function:

Phase boundaries are only available for limited values:

Arithmetical operations cannot be carried out on Missing entries:

Remove the Missing entries before performing operations:

Neat Examples  (4)

Vapor Pressure Formula  (1)

Find the critical temperature and pressure:

Find the phase boundary between vapor and liquid:

Derive an algebraic form for phase boundary:

Find the accuracy of the fit:

Pressure Volume Diagram  (1)

Consider 1 mole of water:

Make a diagram around the critical point:

The straight‐line segments arise in the region where gas and liquid coexist.

Show this region together with the curves:

Use the isotherm to estimate the van der Waals equation parameters and :

In the gas‐liquid coexisting region, the isotherms of the van der Waals equation are nonmonotonic and represent unstable or unphysical behavior, and must be replaced using the Maxwell construction:

Water Fluctuations  (1)

Given a larger volume of water at room temperature and standard air pressure, how much does the number of water molecules within 1 cm^3 fluctuate over time?

Within the grand canonical ensemble, you can derive the following relation for the root mean square of the particle fluctuations as , where is the water density:

Calculating as a finite difference, the fluctuations are about 45 billion water molecules:

Joule–Thomson Coefficient  (1)

Calculate the Joule–Thomson coefficient for compressed gases that, using implicit differentiation, can be obtained from :

The partial derivatives are numerically approximated:

Hydrogen and helium can have negative Joule–Thomson coefficients and get warmer after expansion:

Wolfram Research (2014), ThermodynamicData, Wolfram Language function, https://reference.wolfram.com/language/ref/ThermodynamicData.html.

Text

Wolfram Research (2014), ThermodynamicData, Wolfram Language function, https://reference.wolfram.com/language/ref/ThermodynamicData.html.

CMS

Wolfram Language. 2014. "ThermodynamicData." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/ThermodynamicData.html.

APA

Wolfram Language. (2014). ThermodynamicData. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ThermodynamicData.html

BibTeX

@misc{reference.wolfram_2024_thermodynamicdata, author="Wolfram Research", title="{ThermodynamicData}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/ThermodynamicData.html}", note=[Accessed: 21-December-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_thermodynamicdata, organization={Wolfram Research}, title={ThermodynamicData}, year={2014}, url={https://reference.wolfram.com/language/ref/ThermodynamicData.html}, note=[Accessed: 21-December-2024 ]}