Introduction

Electromagnetic diffraction is a phenomenon that occurs when an electromagnetic (EM) wave passes trough an obstacle or aperture. For EM diffraction the electric or magnetic field are described by a complex function. In the case of two or more apertures the spatial distribution of the EM field after the aperture, called the diffraction pattern, is characterized by fringes that vary with the distance between apertures due to the spatial phase difference. This feature is greatly exploited in metrology to measure distance of micro and nano objects.

In isotropic and non-dispersive media, diffraction of EM waves can be modeled by the vector valued source-free Helmholtz partial differential equation [Jackson, 1999]:

Here is the wave number in the medium and is related to the wavelength by . The wavelength in a medium with refractive index is related to free space wavelength by . In some cases only one component of the field is required to describe the full behavior of the field, in that case the field is said to be scalar. The scalar case was studied in the "Single Aperture Scalar Diffraction" tutorial. In this tutorial we will give a short introduction to multiple slits with a scalar approach and then we will focus on the vector properties of EM waves.

Polarization is a property of transverse vector fields that specifies the geometric orientation of the oscillations. These property is exploited in a technique called polarimetry to characterize optically active samples.

As a prerequisite for the content presented in here, it is recommended to work through the material presented in "Single Aperture Scalar Diffraction" as the basics of electromagnetic diffraction and perfectly matched layer are described in there.

Many of the animations of the simulation results shown in this notebook are generated with a call to Rasterize. This is to reduce the disk space this notebook requires. The downside is that the visual quality of the animations will not be as crisp as without it. To obtain high quality graphics remove or comment out the call to Rasterize.

The symbols and corresponding units used throughout this tutorial are summarized in the Nomenclature section.

Scalar diffraction by multiple apertures

Before modeling the vector Helmholtz equation (1), lets solve the simpler case of scalar diffraction by multiple apertures. This will help to introduce the boundary conditions and element mesh functionalities in a more understandable way.

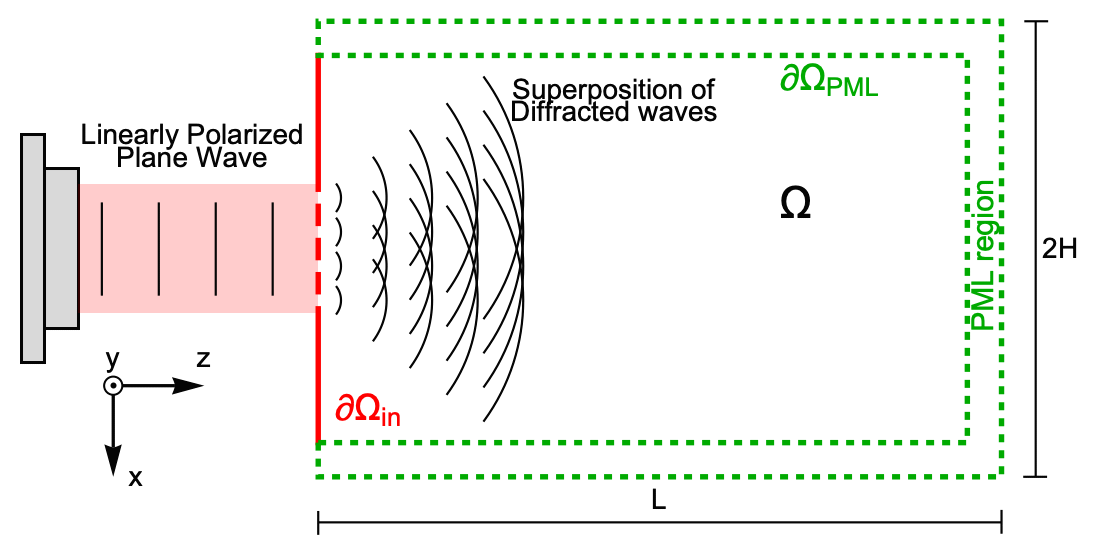
For this first example, consider a laser radiating an electromagnetic (EM) field propagating in the direction and polarized in the direction. Under those conditions the vector electric field can be consider as a scalar field containing energy only in the component [Born & Wolf, 1999].

This application example considers a Helium-Neon laser with a free space wavelength illuminating an opaque screen with 4 evenly spaced apertures of width of and separation . The apertures are slits assumed to be infinitely large in the direction, so there will be no disturbances to the diffracted wave in the direction, hence we can model the system in 2D. The laser and apertures itself will be modelled by a radiation boundary condition on the boundary. The opaque screen is made of a fully absorbing material where light cannot be transmitted or reflected. The boundary indicates the beginning of the perfectly matched layer (PML) region. The PML region is an artificial boundary that absorbs incoming light to mimic an open system where light propagates indefinitely without any reflections [Jin, 1993], therefore the only source of light is the aperture as the field is in the other boundaries. The simulation domain then has dimensions and . The refractive index inside the propagation region is 1.

The scheme above is rotated 90 degrees for better visualization, in the following the propagation axis will be the vertical axis. Also note, that the geometry is symmetric along the direction and that the directions points outwards from the screen.

Domain

To make use of PML approach, the propagation region has to be extended by an extra layer of length which will be the PML region. In this region the incoming wave will be damped out.

Boundaries 1 and 3 (dotted green) describe the outer and inner boundaries of the PML region. Boundaries with marker 4 (orange) are needed to setup the PML parameters. The boundary 2 (red) describes the opaque screen and apertures. To distinguish between the opaque screen and apertures we will use a function inside the Neumann boundary condition.

From the "Single Aperture Scalar Diffraction" tutorial we learn that the intensity profiles in regions far away from the axis are negligible. We can use a MeshRefinementFunction to create a finer mesh in areas with specific coordinates and "RegionMarker" to split the PML region into 4 subregions. A MeshRefinementFunction in 2D works with the element area. We can approximate the mesh's triangle elements area with the area of an equilateral triangle. The area of an equilateral triangle with edge length is .

It is worth mentioning that is a recommended initial discretization constraint to properly resolve the EM wave [Jin, 1993]. In some systems a smaller constants has to be used to provide a precise result.

Now, create the mesh with a maximum element area depending on the position. In the region we will use the recommended edge length as it is our region of interest. Outside that region, the field is practically 0 therefore we will use a larger edge length to reduce the number of unknowns for the FEM method.

The use of Rasterize above helps to reduce the size of the graphics. For a better visual appearance the Rasterize can be removed.

Parameters setup

The basics of PML are described in the acoustic time and frequency domain tutorials. Roughly speaking, a PML region mimics an absorbing material with an absorbing coefficient . While is set inside the propagation region , an increasing function with maximum value is set inside de PML region [Jin, 1993] and there dampens the wave out.

The use of Rasterize above helps to reduce the size of the graphics. For a better visual appearance the Rasterize can be removed.

In the plots we can see that the absorbing coefficient behaves as a wall in the each direction outside the region while leaving the electric field unchanged inside the region .

Boundary conditions

The incoming wave illuminating the boundary containing the opaque screen and aperture can be modelled with a radiation boundary condition of the form [Jin, 1993]:

with the boundary normal, the incoming EM wave propagation direction and the EM wave amplitude. The boundary condition is a sum of two terms, a light incidence term and an absorbing boundary condition term .

The second term is needed to ensure that the boundary does not reflect EM waves and only the incident light flows outward from the boundary. In this case, both, the boundary normal and the wave propagation direction, are in the z-direction, therefore the inner product is 1. will be used to distinguish between the screen and apertures. We can see from (2) that if we set to 0 we only obtain the absorbing term representing an opaque screen, but if we set to it will represent an aperture with initial amplitude .

where is the number of apertures, is the width of each aperture and distance between the centers of any two apertures.

Now, set up the radiation boundary condition with the following parameters , , and .

Model Evaluation

Visualization

See this note about improving the visual quality of the animation.

Model verification

Next, the solution is verified against an analytical solution. To verify the model we can use the integral diffraction formula deduced by Green's method [Ishimarou, 1991]. In 2D the analytical solution is:

where is the euclidian distance between any point at and a point inside the region . As the aperture is a line, the normal is a vector in the direction. For a detailed deduction follow [Ishimarou, 1991].

A more detailed discussion about the analytical solution is given in "Single Aperture Scalar Diffraction" tutorial.

Vector field diffraction

In the above section we have described the diffraction of scalar fields through an object. Scalar fields have a single value at each point in space. On the other hand, vector field have an amplitude and a direction, therefore the field can be written as with the amplitude and the orientation or polarization angle.

In a medium with a diagonal relative permittivity tensor the components of the electric field are independent and can be solved individually [Born & Wolf, 1999].

In the following we will model the diffraction of a vector field by two apertures with a linear polarizer in each one. A linear polarizer is an optical filter instrument that only allows EM waves with a specific polarization angle to pass through. The polarizer angle is called the transmission axis.

For example, when an EM wave with a polarization angle pass through a linear polarizer with transmission axis , the EM wave polarization angle after the polarizer will be , but with a reduced intensity. The intensity will be and the remaining intensity will be absorbed by the polarizer. This is called the Malus' law. One important note, is that if and are orthogonal () the final intensity will be zero.

A linear polarizer with transmission axis is characterized by a transmission matrix [Born & Wolf, 1999].

Assume that the linear polarizer located at the upper aperture is fixed at , i.e. only the x-component of the incident field passes through the aperture. The other polarizer located at the lower aperture has a variable transmission axis .

The scheme above is rotated 90 degrees for better visualization, in the following the propagation axis will be the vertical axis. Also note, that the directions points outwards from the screen.

Parameter setup

Set up the vector Helmholtz operator for the field and the diagonal anisotropic (orthotropic) permittivity for the PML region. In this case an additional rank 3 tensor is needed to set up both PDEs simultaneously, see the DiffusionPDETerm reference page for more information.

Domain definition

The same domain, ElementMesh and PML parameters are used as for the 2D PML scalar example presented above.

Boundary conditions

Before setting up the boundary conditions for the apertures with the linear polarizers, we need to create an auxiliary function for the polarizer transmission matrix.

Now, we can use the same approach as in the scalar example. Set up a function for the amplitude for each aperture. In this case the amplitude is not a scalar, it is a 2D vector. As linear polarizer is placed in each aperture, one with transmission axis at 0° and the other has an arbitrary transmission axis , we need to multiply the transmission matrix to the incoming vector field amplitude.

is the width and is the spacing between the two apertures center.

See this note about improving the visual quality of the animation.

Model Evaluation

For this example we will use the same mesh element and PML regions used in the 2D PML example.

Now, do a sweep for different values of between and .

See this note about improving the visual quality of the animation.

When both apertures have the same polarization and we obtain a result equal to the scalar case studied previously. When starts increasing, the component of the EM wave going out of the upper aperture will interfere with the component of the EM wave going out of the lower aperture. The amount of energy in the component varies with . In the other hand, The EM wave going out the upper aperture does not contain energy in the component, therefore the component of the EM wave going out of the lower aperture does not interfere with anything, producing a single slit pattern which magnitude varies with . When the fields diffracted at the upper and lower aperture are orthogonal, therefore we see two single aperture patterns.

The intensity of the field will be proportional to the sum of the squares of all the components i.e ℐ∝E_x²+E_y².

Nomenclature

References

1.  Born, M. and Wolf, E.(1999). Principles of Optics: Electromagnetic Theory of Propagation, Interference and Diffraction of Light (7th ed.). Cambridge: Cambridge University Press.

2.  Jackson, John D. Classical Electrodynamics. New York :Wiley, 1999.

3.  Jin, Jian-Ming. The finite element method in electromagnetics. John Wiley & Sons, 2015.

4.  A. Ishimarou, Electromagnetic Wave Propagation, Radiation, and Scattering, Prentice Hall, 1991.