Single aperture scalar diffraction
| Introduction | Perfectly matched layers in 3D domains |
| Helmholtz equations in electromagnetism | Nomenclature |
| 2D scalar diffraction model | References |
| Perfectly matched layers in 2D |
Introduction
The phenomenon of diffraction is fully described by the wave equation. The Huygens-Fresnel principle states that when a wave passes through an obstacle or aperture every point surrounding the obstacle or inside the aperture acts as point source of spherical waves. The superposition of those waves produces a wavefront with a characteristic shape [Born & Wolf, 1999]. The intensity profile ℐ [W/m2] of the wavefront is proportional to the electric and magnetic fields cross product magnitude|E×H|2 and it is called the diffraction pattern.
Diffraction is the basic phenomena behind several modern systems used for sensing and imaging, such as Holographic-microscopy, crystallography and astronomical observatories. Solving the wave equation is a relevant engineering problem, particularly in systems with sizes comparable with the electromagnetic wavelength 
, where integral methods such as Fourier transforms are not accurate [Born & Wolf, 1999].
Many of the animations of the simulation results shown in this notebook are generated with a call to Rasterize. This is to reduce the disk space this notebook requires. The downside is that the visual quality of the animations will not be as crisp as without it. To obtain high quality graphics remove or comment out the call to Rasterize.
The symbols and corresponding units used throughout this tutorial are summarized in the Nomenclature section.
Helmholtz equations in electromagnetism
In isotropic and non-dispersive media, diffraction can be modeled by the vector valued source-free Helmholtz partial differential equation [Jackson, 1999]:
Here 
is the wave number in the medium 
and is related to the wavelength 
by 
. The wave number in a material is related to the free space wave number 
by 
with 
the relative permeability and 
the relative permittivity of the material. 
and 
are a measure of the magnetization and polarization of a material [Jackson, 1999]. In general 
and 
are second rank tensors. In isotropic materials 
and 
are scalar constants.
As a first approach to numerically solve equation (1), only one component of the electric field is considered. In Cartesian coordinates the Laplacian of a vector field is the Laplacian of each component ∇2A=(∇2Ax,∇2Ay,∇2Az), therefore equation (2) is a set of 3 independent scalar differential equations. It is worth mentioning that this holds only for materials with diagonal 
and 
tensors. In anisotropic materials with off-diagonal components the PDE could have mixed dependent variables.
It can be shown that the electric field vector describing the field oscillation direction is always perpendicular to the EM wave propagation direction [Born & Wolf, 1999]. This means that an EM wave propagating in the 
direction will only contain energy in the 
and 
components.
In the case that the field can be described by only one component, for example, in linearly polarized EM waves, the field is said to be a scalar quantity.
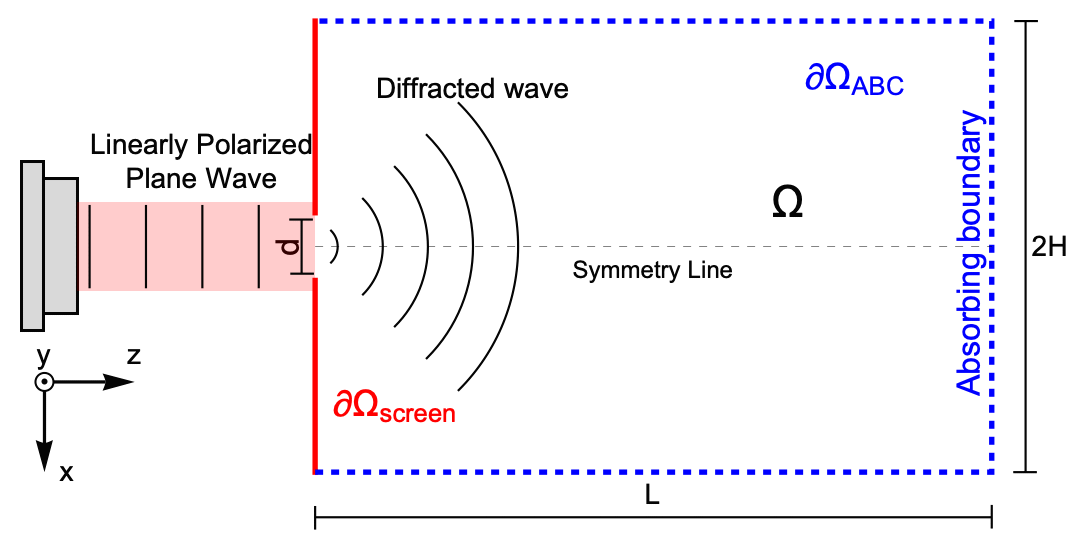
2D scalar diffraction model
This application example considers a Helium-Neon laser with a free space wavelength 
illuminating an opaque screen with an aperture width of 
. The aperture is a slit and assumed to be infinitely large in the 
direction so there will be no disturbances to the diffracted wave in the 
direction, hence we can model the system in 2D. The laser and aperture itself will be modelled by a radiation boundary condition. The opaque screen is made of a fully absorbing material where light cannot be transmitted or reflected. The boundary 
is an artificial boundary that absorb incoming light to mimic an open system where light propagates indefinitely without any reflections, therefore the only source of light is the aperture as the field is 
in the other boundaries. The simulation domain then has dimensions 
and 
. The laser emits 
polarized plane waves in the 
direction. In a 
polarized EM field there is no energy in the 
component. The refractive index inside the region 
is 1.
The scheme above is rotated 90 degrees for better visualization, in the following the propagation 
axis will be the vertical axis. Also note, that the geometry is symmetric along the 
direction and that the 
directions points outwards from the screen.
Parameters setup
Set up the incoming scalar EM wave parameters and the Helmholtz differential operator in equation (3) for the diffracted scalar wave 
.
The differential operator is in Inactive form to allow for NeumannValue boundary conditions. For more information read the Formal Partial Differential Equation section.
We could very well have made use of the HelmholtzPDEComponent to set the PDE model up. However, at a later stage we will be making use of perfectly matched layers and then the HelmholtzPDEComponent is less practical. To make the workflow consistent between the sections we choose to the model the PDE with the basic PDE modeling terms.
Domain
Next, the simulation domain is set up. The simulation domain 
is symmetric with axis of symmetry being the 
axis so it is sufficient to simulate half the domain in the x direction.
The black numbers are the boundary element markers. Marker 1 is assigned to the symmetry line boundary (dashed line), marker 2 indicates the 
boundary (blue lines), marker 3 is the 
boundary (red line) and marker 4 represents half of the aperture boundary that we will call 
(black line) from now on. Recall that 
is an opening but the incident light is modelled by a boundary condition there.
Now, an element mesh is created from the boundary mesh. Normally, five elements per wavelength is enough to resolve the wave [Jin, 1993]. It is worth mentioning that 
is a recommended initial discretization constraint. In some systems a smaller constant has to be used to provide a precise result. In this case we will use 
to obtain a smoother curve.
Boundary conditions
All that is left, is to set up the conditions for each boundary. Following the theory, the boundary 
should be at infinity to eliminate all contributions due to reflections in the boundary [Jin, 1993]. Since the solution over an infinitely larger domain can not be computed an artificial absorbing boundary has to be placed on the edge 
to avoid reflections. The absorbing boundary condition can also be used for 
as it is an opaque screen that absorbs all the incoming light. Using a first order Padé absorbing boundary condition (ABC) [Jin, 1993].
More information about absorbing boundary conditions and radiation conditions can be found in Acoustics in the Time Domain.
The incoming wave illuminating the aperture in 
can be modelled with a radiation boundary condition of the form:
with 
the boundary normal, 
the incoming EM wave propagation direction and 
the EM wave amplitude. The boundary condition is a sum of two terms, a light incidence term 
and an absorbing boundary condition term 
.
The second term is needed to ensure that the boundary 
does not reflect EM waves and only the incident light flows outward from the boundary. In this case, both, the boundary normal and the wave propagation direction, are in the z-direction, therefore the inner product is 1. 
will be set to 1.
The axis of symmetry on the element boundary marker 1 can be modeled with a Neumann 0 value. This is the default boundary condition if nothing else is specified on a boundary.
Model evaluation
Compute the numeric solution of the PDE with NDSolve.
Visualization
See this note about improving the visual quality of the animation.
See this note about improving the visual quality of the image.
The intensity plot above shows that the electric field concentrates around the 
axis, therefore using an overly fine mesh far away from the center region may be unnecessarily computationally expensive. A variable max cell measure, set up with a MeshRefinementFunction, can reduce the number of mesh elements while conserving precision in relevant regions.
As indicated above, absorbing boundary conditions (
) are an approximate boundary condition to model infinite domains. In the plot above, fluctuations can be seen as 
approaches 
. These fluctuations are due to undesired reflections at the absorbing boundary condition. In the following section a different, more accurate, approach to truncate the computational domain of an open system is introduced.
Perfectly matched layers in 2D
Absorbing boundary conditions 
, like used above, are not a perfect absorbing boundary. Some reflection may occur when the incidence angles of the wave deviates too much from the surface normal [Jin, 1993]. As a result, undesired fluctuations can appear. A better approach to truncate the computational domain are perfectly matched layers (PML).
The basic ideal of PML is to add an additional layer around the simulation domain that is highly absorptive. As soon as the wave leaves the regular simulation domain and enters the PML the wave will be attenuated quickly. A PML layer can be understood as a highly absorbing inhomogeneous orthotropic material. Orthotropic materials are a sub group of anisotropic materials where only the main directions 
of a material differ but not the off diagonal directions so 
. In our case orthotropic materials are described by a position dependent permittivity tensor 
. In absorbing media the relative permittivity is complex valued 
, where 
describes the medium's polarizability and 
the absorptive properties of the material. In the 2D model we are only using 
for the x and z directions.
A more detailed introduction to PML can be found in the acoustic time and frequency domain tutorials.
Domain
To make use of PMLs the physical region 
needs to be extended by an extra layer of length 
which will be the PML region. In this region the incoming wave will be damped out.
Boundaries 1 to 4 are the same as before, but now boundaries 2 are not absorbing boundary conditions as we are truncating the domain with a PML region. Boundaries with marker 5 (green) are the end of the PML region and boundaries with marker 6 (orange) are needed to define 3 separate regions with different PML parameters.
Earlier we created an uniform element mesh with a constant max cell measure, but we saw from the intensity profiles that the intensity in regions far away from the 
axis are negligible. We can use a MeshRefinementFunction to create a finer mesh in areas with specific coordinates and set up region markers for the PML regions. A MeshRefinementFunction in 2D works with the element area. We can approximate the mesh's triangle elements area with the area of an equilateral triangle. The area that fulfils the 
constraint is 
.
The use of Rasterize above helps to reduce the size of the graphics. For a better visual appearance the Rasterize can be removed.
Parameter setup
As the PML layer 
is a diagonal tensor we can still use (4). Inside the physical region 
and 
to obtain the same PDE as in the initial example. In the PML region 
will be an increasing function with maximum value 
.
.
The use of Rasterize above helps to reduce the size of the graphics. For a better visual appearance the Rasterize can be removed.
In the 
function plots we see that the absorbing coefficient behaves as a wall in the each direction outside the region 
while leaving the electric field unchanged inside the region 
.
Boundary conditions
Using the same boundary conditions for the incident light boundary and screen. Recall that absorbing boundary conditions 
are not needed now.
Boundaries 1, 2, 5 and 6 will have the default Neumann 0 value.
Model Evaluation
Visualization
See this note about improving the visual quality of the animation.
As 
approaches 
no fluctuations are present with the PML approach.
As we can see there is a kind of regular fluctuating error between the two approaches. This is a result of the undesired reflections caused by the absorbing boundaries.
Model verification
So far we have compared the numerical solution of the absorbing boundary condition approach and the perfectly matched layer (PML) approach. Next, the PML solution is verified against an analytical solution. To verify the model we can use the integral diffraction formula deduced with the Green's method [Ishimarou, 1991].
where 
is a surface enclosing the region of interest, 
is the Green function of the system and 
is the normal derivative. The integral can be solved using 3 different types of boundary conditions (BC) for 
. Dirichlet 
or Neumann 
BC, often called type 1 or 2 Sommerfeld's conditions respectively, or both Dirichlet and Neumann BC which is called Kirchhoff's boundary condition [Wolf & Marchand, 1964]. Although Kirchhoff's BC are the most commonly used, it is mathematically inconsistent as the assumed BC are not retrieved from the solution [Wolf & Marchand, 1964]. It is worth mentioning that all three BC give the same result in the far field [Wolf & Marchand, 1964].
In practice, the integration is not done along the entire surface, as explained in the 2D scalar diffraction model section. Only the 
boundary contributes to the integral. In 2D the Green function is a Hankel function of second kind of order 0. Additionally we will make use of type 1 Sommerfeld's condition [Ishimarou, 1991]. The theoretical solution is:
where 
is the euclidian distance between any point 
at 
and a point 
inside the region 
. As the aperture is a line, the normal is a vector in the 
direction.
.The discrepancy between the theoretical and numerical near 
can be attributed to the fact that the analytical solution do not retrieve the imposed BC, for instance, the Sommerfeld type 1 integral present divergences near the 
plane. Also, Recall that the aperture boundary condition is the sum of light incidence and absorbing boundary conditions. This approximate absorbing boundary condition term in the radiation boundary condition 
may cause some fluctuations starting from 
. Also note that these fluctuations reduce the further the wave travels into the domain.
For more information about the analytical solution and Kirchhoff-Sommerfeld approaches see [Buchwald & Yeang, 2016][Totzeck, 1991][Heurtley, 1973].
As a note, the high frequency fluctuations in the error plot along the propagation direction can be eliminated by decreasing mesh element length to 
.
Perfectly matched layers in 3D domains
In the last section we implemented a 2D PML. Now, we will calculate the diffraction of waves by a 2D circular aperture in a 3D domain. Calculating 3D regions can be computationally expensive, therefore we will restrict ourselves to the case when we can use the symmetry of the system to only calculate some part of the domain.
Set up the incoming scalar EM wave parameters to 
and the 3D Helmholtz differential operator with the orthotropic relative permittivity for the 3D PML region. The diffracted scalar wave will be labeled 
.
First, set up a cubic domain in the positive octant including the PML region, use OpenCascadeLink to join the regions conserving the inner boundaries.
The OpenCascadeLink tutorial has more detailed information on generating objects with internal boundaries.
The green boundaries enclose the PML volume, the blue boundaries are the symmetry planes and the Red plane contains 
of the 
and 
boundaries. The yellow disk represents one quarter of the aperture. In some cases, it is hard to create separate boundaries for the aperture and screen, therefore we will use a function to set up the radiation and absorbing boundary condition at the same time in the red plane.
In this case the MeshRefinementFunction will dependent on the volume of the mesh element. In this case we will use the recommended 
edge length. The volume for the TetrahedronElement could be calculated as 
to fulfil the 
edge length constraint.
axis.See this note about improving the visual quality of the image.
We can see that the mesh is finer near the left corner and becomes coarser at the upper right corner. Note that the aperture depicted in yellow is not part of the mesh but for visualization only.
Visualizing 3D meshes can be complicated. A Manipulate provides an easier way to visualize the 3D regions and ElementMarker in 3D individually. To reduce the size of this notebook a second element mesh is generated for visualization purposes only.
Visualize the boundary element markers groups to find the ElementMarker for the aperture.
Earlier we split the 
and 
boundaries, but it can be difficult to set up the proper boundaries when working with more complex geometries or 3D regions. A better approach for those cases is to use a function to distinguish between the conditions 
and 
. From equation (5) we can see that if we set 
to 
we recover equation (6), therefore we can set both conditions 
and 
with a function that is 
at the aperture and 
at the screen.
The next step is to create a function for a circular aperture of diameter 
.
Now we can create the unified boundary condition 
.
The surface boundaries with ElementMarker 1 and 5 are the surfaces of symmetry for this region and can be modeled with a Neumann 0 value. This is the default boundary condition if nothing else is specified on a boundary.
Perfectly matched layer parameter setup
Knowing the region markers, the PML absorbing coefficients can now be set up.
Model Evaluation
Visualization
See this note about improving the visual quality of the animation.
See this note about improving the visual quality of the animation.
The density plot shows the characteristic ring-like pattern of circular apertures. For long propagation distances this pattern will evolve into a order 0 Bessel function of the first kind.
Model verification
In 3D the green function of the system are spherical waves of the form 
. Replacing the green function in equation (7) we obtain:
where 
is the euclidian distance between any point 
at 
and a point 
inside the region 
. To make use of the analytical result we set up a helper function.
As a summary, absorbing boundary conditions (ABCs) are useful for a quick problem setup but if accuracy is essential perfectly matched layers (PMLs) are a better choice.
Nomenclature
| Symbol | Description | Unit |
| E | Electric field | [V/m] |
| λn | Wavelength | [m] |
| kn | Wave number | [1/m] |
| μr | Relative permeability | N/A |
| ϵr | Relative Permittivity | N/A |
| L | Propagation region length | [μm] |
| H | Propagation region width | [μm] |
| d | Aperture size | [m] |
| Γscreen | Opaque screen boundary | N/A |
| Γaperture | Aperture boundary | N/A |
| ΓABC | Absorbing Boundary | N/A |
| Ω | Propagation region | N/A |
References
1. Born, M. and Wolf, E.(1999). Principles of Optics: Electromagnetic Theory of Propagation, Interference and Diffraction of Light (7th ed.). Cambridge: Cambridge University Press.
2. Jackson, John D. Classical Electrodynamics. New York :Wiley, 1999.
3. Jin, Jian-Ming. The finite element method in electromagnetics. John Wiley & Sons, 2015.
4. A. Ishimarou, Electromagnetic Wave Propagation, Radiation, and Scattering, Prentice Hall, 1991.
5. Wolf, E., & Marchand, E. W. Comparison of the Kirchhoff and the Rayleigh–Sommerfeld Theories of Diffraction at an Aperture. Journal of the Optical Society of America, 1964, 54(5), 587. doi:10.1364/josa.54.000587
6. Buchwald, J.Z., Yeang, CP. Kirchhoff’s theory for optical diffraction, its predecessor and subsequent development: the resilience of an inconsistent theory. Arch. Hist. Exact Sci. 70, 463–511 (2016). https://doi.org/10.1007/s00407-016-0176-1
7. Totzeck, M. (1991). Validity of the scalar Kirchhoff and Rayleigh–Sommerfeld diffraction theories in the near field of small phase objects. Journal of the Optical Society of America A, 1991, 8(1), 27. doi:10.1364/josaa.8.000027
8. Heurtley, J. C. Scalar Rayleigh–Sommerfeld and Kirchhoff diffraction integrals: A comparison of exact evaluations for axial points*. Journal of the Optical Society of America, 1973, 63(8), 1003. doi:10.1364/josa.63.001003