HelmholtzPDEComponent

HelmholtzPDEComponent[vars,pars]

yields a Helmholtz PDE term with model variables vars and model parameters pars.

Details

  • HelmholtzPDEComponent returns a sum of differential operators to be used as a part of partial differential equations:
  • HelmholtzPDEComponent can be used to model Helmholtz equations with dependent variable 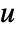, independent variables 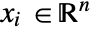and time variable .
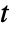  • Stationary model variables vars are vars={u[x1,…,xn],{x1,…,xn}}.
  • Time-dependent model variables vars are vars={u[t,x1,…,xn],t,{x1,…,xn}}.
  • The HelmholtzPDEComponent is based on a diffusion and reaction term:

    • del .(1 del u(x))^(︷^( diffusion term )) +k^2 u(x)^(︷^( reaction term ))

  • The Helmholtz PDE term 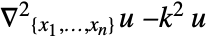is realized as a DiffusionPDETerm with –1 as diffusion coefficient and a ReactionPDETerm with coefficient 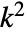, resulting in .
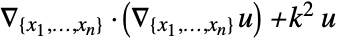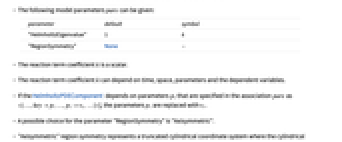
  • The following model parameters pars can be given:
  • parameterdefaultsymbol
    "HelmholtzEigenvalue"1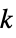
    "RegionSymmetry"None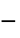
  • The reaction term coefficient 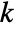is a scalar.
  • The reaction term coefficient 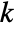can depend on time, space, parameters and the dependent variables.
  • If the HelmholtzPDEComponent depends on parameters 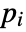that are specified in the association pars as …,keypi…,pivi,…], the parameters 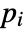are replaced with .
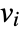  • A possible choice for the parameter "RegionSymmetry" is "Axisymmetric".
  • "Axisymmetric" region symmetry represents a truncated cylindrical coordinate system where the cylindrical coordinates are reduced by removing the angle variable as follows:
  • dimensionreductionequation
    1D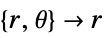
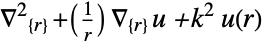
    2D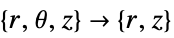
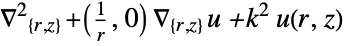
  • The diffusion coefficient 1 affects the meaning of NeumannValue.
  • If the HelmholtzPDEComponent depends on parameters 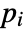that are specified in the association pars as …,keypi…,pivi,…, the parameters 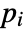are replaced with .

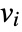Examples

open allclose all

Basic Examples  (4)

Define a Helmholtz equation:

Activate the equation:

Define a Helmholtz equation with a symbolic coefficient:

Define a Helmholtz equation with an eigenvalue of 2:

Confirm the first eigenvalue of a Helmholtz PDE term specified to have an eigenvalue of 2:

Scope  (1)

Define a 2D axisymmetric Helmholtz equation:

Activate the equation:

Wolfram Research (2020), HelmholtzPDEComponent, Wolfram Language function, https://reference.wolfram.com/language/ref/HelmholtzPDEComponent.html (updated 2022).

Text

Wolfram Research (2020), HelmholtzPDEComponent, Wolfram Language function, https://reference.wolfram.com/language/ref/HelmholtzPDEComponent.html (updated 2022).

CMS

Wolfram Language. 2020. "HelmholtzPDEComponent." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2022. https://reference.wolfram.com/language/ref/HelmholtzPDEComponent.html.

APA

Wolfram Language. (2020). HelmholtzPDEComponent. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/HelmholtzPDEComponent.html

BibTeX

@misc{reference.wolfram_2025_helmholtzpdecomponent, author="Wolfram Research", title="{HelmholtzPDEComponent}", year="2022", howpublished="\url{https://reference.wolfram.com/language/ref/HelmholtzPDEComponent.html}", note=[Accessed: 21-February-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_helmholtzpdecomponent, organization={Wolfram Research}, title={HelmholtzPDEComponent}, year={2022}, url={https://reference.wolfram.com/language/ref/HelmholtzPDEComponent.html}, note=[Accessed: 21-February-2025 ]}