AcousticPDEComponentCopy to clipboard.
✖
AcousticPDEComponent
yields an acoustic PDE term component with variables vars and parameters pars.
Details
- AcousticPDEComponent returns a sum of differential operators to be used as a part of partial differential equations:
- AcousticPDEComponent models the propagation of sound in isotropic media in both the time and frequency domain by mechanisms such as diffusion.
- AcousticPDEComponent models acoustic phenomena in fluids with dependent variable pressure
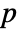[![TemplateBox[{InterpretationBox[, 1], "Pa", pascals, "Pascals"}, QuantityTF]](Files/AcousticPDEComponent.en/4.png "TemplateBox[{InterpretationBox[, 1], \"Pa\", pascals, \"Pascals\"}, QuantityTF]")
], independent variables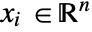 
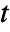[![TemplateBox[{InterpretationBox[, 1], "m", meters, "Meters"}, QuantityTF]](Files/AcousticPDEComponent.en/6.png "TemplateBox[{InterpretationBox[, 1], \"m\", meters, \"Meters\"}, QuantityTF]")
] and time variable 
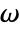[![TemplateBox[{InterpretationBox[, 1], "s", seconds, "Seconds"}, QuantityTF]](Files/AcousticPDEComponent.en/8.png "TemplateBox[{InterpretationBox[, 1], \"s\", seconds, \"Seconds\"}, QuantityTF]")
] or frequency variable 
[![TemplateBox[{InterpretationBox[, 1], {"rad", , "/", , "s"}, radians per second, {{(, "Radians", )}, /, {(, "Seconds", )}}}, QuantityTF]](Files/AcousticPDEComponent.en/10.png "TemplateBox[{InterpretationBox[, 1], {\"rad\", , \"/\", , \"s\"}, radians per second, {{(, \"Radians\", )}, /, {(, \"Seconds\", )}}}, QuantityTF]")
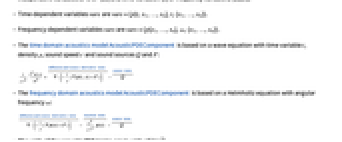
]. - Time-dependent variables vars are vars={p[t,x1,…,xn],t,{x1,…,xn}}.
- Frequency-dependent variables vars are vars={p[x1,…,xn],ω,{x1,…,xn}}.
- The time domain acoustics model AcousticPDEComponent is based on a wave equation with time variable
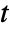, density 
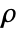, sound speed 
and sound sources 
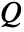and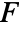 
: - The frequency domain acoustics model AcousticPDEComponent is based on a Helmholtz equation with angular frequency
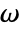: - The units of the acoustic PDE terms are in units of [1/
![TemplateBox[{InterpretationBox[, 1], {{"s", ^, 2}}, seconds squared, {"Seconds", ^, 2}}, QuantityTF]](Files/AcousticPDEComponent.en/19.png "TemplateBox[{InterpretationBox[, 1], {{\"s\", ^, 2}}, seconds squared, {\"Seconds\", ^, 2}}, QuantityTF]")
]. - The following parameters pars can be given:
-
parameter default symbol "DipoleSource" {0,…}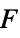 
, dipole source [![TemplateBox[{InterpretationBox[, 1], {"N", , "/", , {"m", ^, 3}}, newtons per meter cubed, {{(, "Newtons", )}, /, {(, {"Meters", ^, 3}, )}}}, QuantityTF]](Files/AcousticPDEComponent.en/21.png "TemplateBox[{InterpretationBox[, 1], {\"N\", , \"/\", , {\"m\", ^, 3}}, newtons per meter cubed, {{(, \"Newtons\", )}, /, {(, {\"Meters\", ^, 3}, )}}}, QuantityTF]")
]"MassDensity" 1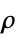 
, density of media [![TemplateBox[{InterpretationBox[, 1], {"kg", , "/", , {"m", ^, 3}}, kilograms per meter cubed, {{(, "Kilograms", )}, /, {(, {"Meters", ^, 3}, )}}}, QuantityTF]](Files/AcousticPDEComponent.en/23.png "TemplateBox[{InterpretationBox[, 1], {\"kg\", , \"/\", , {\"m\", ^, 3}}, kilograms per meter cubed, {{(, \"Kilograms\", )}, /, {(, {\"Meters\", ^, 3}, )}}}, QuantityTF]")
]"Material" Automatic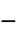 
"MonopoleSource" 0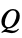 
, monopole source [1/![TemplateBox[{InterpretationBox[, 1], {{"s", ^, 2}}, seconds squared, {"Seconds", ^, 2}}, QuantityTF]](Files/AcousticPDEComponent.en/26.png "TemplateBox[{InterpretationBox[, 1], {{\"s\", ^, 2}}, seconds squared, {\"Seconds\", ^, 2}}, QuantityTF]")
]"RegionSymmetry" None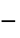 
"SoundSpeed" 1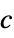 
, speed of sound [![TemplateBox[{InterpretationBox[, 1], {"m", , "/", , "s"}, meters per second, {{(, "Meters", )}, /, {(, "Seconds", )}}}, QuantityTF]](Files/AcousticPDEComponent.en/29.png "TemplateBox[{InterpretationBox[, 1], {\"m\", , \"/\", , \"s\"}, meters per second, {{(, \"Meters\", )}, /, {(, \"Seconds\", )}}}, QuantityTF]")
] - All parameters may depend on any of
, 
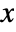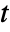and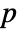 
as well as other dependent variables with the exception of 
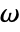, resulting in a nonlinear eigenvalue problem. - AcousticPDEComponent allows for sources in the time domain and sources in the frequency domain.
-
Monopole source,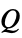 
Copy to clipboard.
✖https://wolfram.com/xid/0d2p3il2o6flb01aecoci6Direct link to exampleDipole source,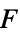 
Copy to clipboard.
✖https://wolfram.com/xid/0d2p3il2o6flb01aecoci6Direct link to example - A monopole source
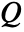models a point source that radiates sound isotropically. - A dipole source
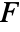models a two-point source that radiates sound anisotropically. - The number of independent variables in
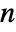specifies the length of 
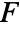. - If no parameters are specified, the default time domain acoustics PDE is
- If no parameters are specified, the default frequency domain acoustics PDE is
- A possible choice for the parameter "RegionSymmetry" is "Axisymmetric".
- "Axisymmetric" region symmetry represents a truncated cylindrical coordinate system where the cylindrical coordinates are reduced by removing the angle variable as follows:
-
dimension reduction equation 1D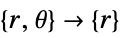 
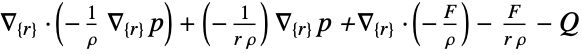
2D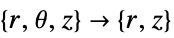 
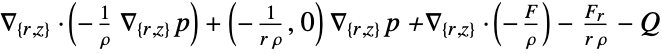
- If the AcousticPDEComponent depends on parameters
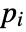that are specified in the association pars as …,keypi…,pivi,…], the parameters 
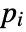are replaced with 
.
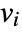Examples
open allclose allBasic Examples (4)Summary of the most common use cases
Define a time domain acoustic PDE term:
https://wolfram.com/xid/0d2p3il2o6flb01aecoci6-nx7oa9
Define a frequency domain acoustic model:
https://wolfram.com/xid/0d2p3il2o6flb01aecoci6-o37aj0
Define model variables vars for a transient acoustic pressure field with model parameters pars:
https://wolfram.com/xid/0d2p3il2o6flb01aecoci6-ff3bvs
Define initial conditions ics of a right-going sound wave 
:
https://wolfram.com/xid/0d2p3il2o6flb01aecoci6-hwck5b
Set up the equation with a sound hard boundary at the right end:
https://wolfram.com/xid/0d2p3il2o6flb01aecoci6-qfm3d2
https://wolfram.com/xid/0d2p3il2o6flb01aecoci6-lts889
Visualize the sound field in the time domain:
https://wolfram.com/xid/0d2p3il2o6flb01aecoci6-6z9t8h
Define model variables vars for a frequency domain acoustic pressure field with model parameters pars:
https://wolfram.com/xid/0d2p3il2o6flb01aecoci6-6xqbpo
Set up the equation with a radiation boundary at the left end:
https://wolfram.com/xid/0d2p3il2o6flb01aecoci6-odt7ku
https://wolfram.com/xid/0d2p3il2o6flb01aecoci6-xht1ym
Visualize the sound field in the frequency domain at various frequencies 
:
https://wolfram.com/xid/0d2p3il2o6flb01aecoci6-6luhf0
Scope (21)Survey of the scope of standard use cases
Basic Examples (2)
Define a time- or frequency-independent acoustic model:
https://wolfram.com/xid/0d2p3il2o6flb01aecoci6-q7jiop
Define a time- or frequency-independent acoustic axisymmetric model:
https://wolfram.com/xid/0d2p3il2o6flb01aecoci6-05k6pi
Time Domain (7)
Define model variables vars for a transient acoustic pressure field with model parameters pars:
https://wolfram.com/xid/0d2p3il2o6flb01aecoci6-dkqzor
Set up initial conditions ics of a right-going plane wave 
:
https://wolfram.com/xid/0d2p3il2o6flb01aecoci6-782st2
Set up the equation with an acoustic absorbing boundary at the right end for a plane wave:
https://wolfram.com/xid/0d2p3il2o6flb01aecoci6-42zqls
https://wolfram.com/xid/0d2p3il2o6flb01aecoci6-mbx188
https://wolfram.com/xid/0d2p3il2o6flb01aecoci6-4vstdx
Define model variables vars for a transient acoustic pressure field with model parameters pars:
https://wolfram.com/xid/0d2p3il2o6flb01aecoci6-rg5ljl
Define initial conditions ics of a right-going plane wave 
:
https://wolfram.com/xid/0d2p3il2o6flb01aecoci6-8oh64a
Set up the equation with an acoustic impedance boundary at the right and an impedance 
of 
:
https://wolfram.com/xid/0d2p3il2o6flb01aecoci6-zve6oh
https://wolfram.com/xid/0d2p3il2o6flb01aecoci6-6qylfk
https://wolfram.com/xid/0d2p3il2o6flb01aecoci6-n1vngk
Define model variables vars for a transient acoustic pressure field with model parameters pars:
https://wolfram.com/xid/0d2p3il2o6flb01aecoci6-jndtki
Define silent initial conditions ics:
https://wolfram.com/xid/0d2p3il2o6flb01aecoci6-zz8xlz
Set up the equation with an acoustic normal velocity boundary with the sound particle velocity v of 
at the left end:
https://wolfram.com/xid/0d2p3il2o6flb01aecoci6-n25z2k
Solve the PDE on a refined mesh:
https://wolfram.com/xid/0d2p3il2o6flb01aecoci6-hpjmye
https://wolfram.com/xid/0d2p3il2o6flb01aecoci6-hb4etn
Define model variables vars for a transient acoustic pressure field with model parameters pars:
https://wolfram.com/xid/0d2p3il2o6flb01aecoci6-xntwvy
Define silent initial conditions ics:
https://wolfram.com/xid/0d2p3il2o6flb01aecoci6-zsqfna
Set up the equation with an acoustic pressure boundary and a pressure source 
of 
at the left end:
https://wolfram.com/xid/0d2p3il2o6flb01aecoci6-4dhl1v
Solve the PDE on a refined mesh:
https://wolfram.com/xid/0d2p3il2o6flb01aecoci6-p4fwvs
https://wolfram.com/xid/0d2p3il2o6flb01aecoci6-tm2q28
Define model variables vars for a frequency domain acoustic pressure field with model parameters pars:
https://wolfram.com/xid/0d2p3il2o6flb01aecoci6-njshna
Define silent initial conditions ics:
https://wolfram.com/xid/0d2p3il2o6flb01aecoci6-2uykky
Set up the equation with an acoustic radiation boundary at the left end, a pressure source 
of 
and a radiation angle 
of 
:
https://wolfram.com/xid/0d2p3il2o6flb01aecoci6-ybech5
https://wolfram.com/xid/0d2p3il2o6flb01aecoci6-bb27yc
https://wolfram.com/xid/0d2p3il2o6flb01aecoci6-d15too
Define model variables vars for a transient acoustic pressure field with model parameters pars:
https://wolfram.com/xid/0d2p3il2o6flb01aecoci6-sc8r2x
Define initial conditions ics of a right-going plane wave 
:
https://wolfram.com/xid/0d2p3il2o6flb01aecoci6-uxipj8
Set up the equation with an acoustic sound hard boundary at the right end:
https://wolfram.com/xid/0d2p3il2o6flb01aecoci6-zs2ic4
https://wolfram.com/xid/0d2p3il2o6flb01aecoci6-4rbcfo
https://wolfram.com/xid/0d2p3il2o6flb01aecoci6-0dsfh7
Define model variables vars for a transient acoustic pressure field with model parameters pars:
https://wolfram.com/xid/0d2p3il2o6flb01aecoci6-uu6toz
Define initial conditions 
of a right-going plane wave 
:
https://wolfram.com/xid/0d2p3il2o6flb01aecoci6-6dfymd
Set up the equation with an acoustic sound soft boundary at the right end:
https://wolfram.com/xid/0d2p3il2o6flb01aecoci6-zhia5e
https://wolfram.com/xid/0d2p3il2o6flb01aecoci6-5r1ftn
https://wolfram.com/xid/0d2p3il2o6flb01aecoci6-8g08wi
Frequency Domain (10)
Define a frequency domain acoustic model with particular sound speed and mass density:
https://wolfram.com/xid/0d2p3il2o6flb01aecoci6-19xw8a
Define a frequency domain acoustic model for a particular material:
https://wolfram.com/xid/0d2p3il2o6flb01aecoci6-479m0m
Define a frequency domain acoustic model for a particular material:
https://wolfram.com/xid/0d2p3il2o6flb01aecoci6-450lar
Define model variables vars for a frequency domain acoustic pressure field with model parameters pars:
https://wolfram.com/xid/0d2p3il2o6flb01aecoci6-dcdeb2
Set up the equation with a radiation boundary at the left end and an acoustic absorbing boundary at the right end:
https://wolfram.com/xid/0d2p3il2o6flb01aecoci6-tgzhoh
https://wolfram.com/xid/0d2p3il2o6flb01aecoci6-h20j7w
Visualize the solution in the frequency domain at various frequencies 
:
https://wolfram.com/xid/0d2p3il2o6flb01aecoci6-kz3jqn
Convert the solution to the time domain:
https://wolfram.com/xid/0d2p3il2o6flb01aecoci6-vrfb1r
Define model variables vars for a frequency domain acoustic pressure field with model parameters pars:
https://wolfram.com/xid/0d2p3il2o6flb01aecoci6-bhl0xg
Set up the equation with a radiation boundary at the left, an acoustic impedance boundary at the right and an impedance 
of 
:
https://wolfram.com/xid/0d2p3il2o6flb01aecoci6-jxvm1d
https://wolfram.com/xid/0d2p3il2o6flb01aecoci6-1tr8dy
Visualize the solution in the frequency domain at various frequencies 
:
https://wolfram.com/xid/0d2p3il2o6flb01aecoci6-hfw83g
Convert the solution to the time domain:
https://wolfram.com/xid/0d2p3il2o6flb01aecoci6-gw1pid
Define model variables vars for a frequency domain acoustic pressure field with model parameters pars:
https://wolfram.com/xid/0d2p3il2o6flb01aecoci6-friucl
Set up the equation with an acoustic normal velocity boundary at the left, the sound particle velocity 
of 
and an acoustic absorbing boundary at the right:
https://wolfram.com/xid/0d2p3il2o6flb01aecoci6-nxequa
https://wolfram.com/xid/0d2p3il2o6flb01aecoci6-j45tbr
Visualize the solution in the frequency domain at various frequencies 
:
https://wolfram.com/xid/0d2p3il2o6flb01aecoci6-twzwts
Convert the solution to the time domain:
https://wolfram.com/xid/0d2p3il2o6flb01aecoci6-f4fyi3
Define model variables vars for a frequency domain acoustic pressure field with model parameters pars:
https://wolfram.com/xid/0d2p3il2o6flb01aecoci6-wx4z87
Set up the equation with an acoustic pressure boundary at the left, a pressure source 
of 
and an acoustic absorbing boundary at the right:
https://wolfram.com/xid/0d2p3il2o6flb01aecoci6-p4wfaa
https://wolfram.com/xid/0d2p3il2o6flb01aecoci6-ohxk8y
Visualize the solution in the frequency domain at various frequencies 
:
https://wolfram.com/xid/0d2p3il2o6flb01aecoci6-6895m5
Convert the solution to the time domain:
https://wolfram.com/xid/0d2p3il2o6flb01aecoci6-jrdfzk
Define model variables vars for a frequency domain acoustic pressure field with model parameters pars:
https://wolfram.com/xid/0d2p3il2o6flb01aecoci6-exrmgh
Set up the equation with an acoustic radiation boundary at the left end, a pressure source 
of 
and a radiation angle 
of 
:
https://wolfram.com/xid/0d2p3il2o6flb01aecoci6-gkaaae
https://wolfram.com/xid/0d2p3il2o6flb01aecoci6-pwe1cl
Visualize the solution in the frequency domain at various frequencies 
:
https://wolfram.com/xid/0d2p3il2o6flb01aecoci6-dy5y5f
Convert the solution to the time domain:
https://wolfram.com/xid/0d2p3il2o6flb01aecoci6-xj6h47
Define model variables vars for a frequency domain acoustic pressure field with model parameters pars:
https://wolfram.com/xid/0d2p3il2o6flb01aecoci6-lkca8y
Set up the equation with an acoustic radiation boundary at the left, a pressure source 
of 
and an acoustic sound hard boundary at the right:
https://wolfram.com/xid/0d2p3il2o6flb01aecoci6-37me12
https://wolfram.com/xid/0d2p3il2o6flb01aecoci6-h50g13
Visualize the solution in the frequency domain at various frequencies 
:
https://wolfram.com/xid/0d2p3il2o6flb01aecoci6-cjxae2
Convert the solution to the time domain:
https://wolfram.com/xid/0d2p3il2o6flb01aecoci6-imjpc3
Define model variables vars for a frequency domain acoustic pressure field with model parameters pars:
https://wolfram.com/xid/0d2p3il2o6flb01aecoci6-qdqm9v
Set up the equation with a radiation boundary at the left end and an acoustic absorbing boundary at the right end:
https://wolfram.com/xid/0d2p3il2o6flb01aecoci6-r4iroh
https://wolfram.com/xid/0d2p3il2o6flb01aecoci6-dok3s9
Visualize the solution in the frequency domain at various frequencies 
:
https://wolfram.com/xid/0d2p3il2o6flb01aecoci6-4qix3
Convert the solution to the time domain:
https://wolfram.com/xid/0d2p3il2o6flb01aecoci6-xn64v6
Units (2)
Set up an acoustic time domain equation for xenon:
https://wolfram.com/xid/0d2p3il2o6flb01aecoci6-wft4av
Set up an acoustic frequency domain model for xenon by specifying material parameters:
https://wolfram.com/xid/0d2p3il2o6flb01aecoci6-yu3azj
Applications (1)Sample problems that can be solved with this function
The following acoustic model describes an open pipe, wherein a vibrating piston is placed inside one end of the pipe while the other end of the pipe opens into an infinite domain. In this case, an impedance boundary condition is placed on one end to model the infinite domain. The pipe that will be modeled is a flanged circular pipe, as shown in the following figure:
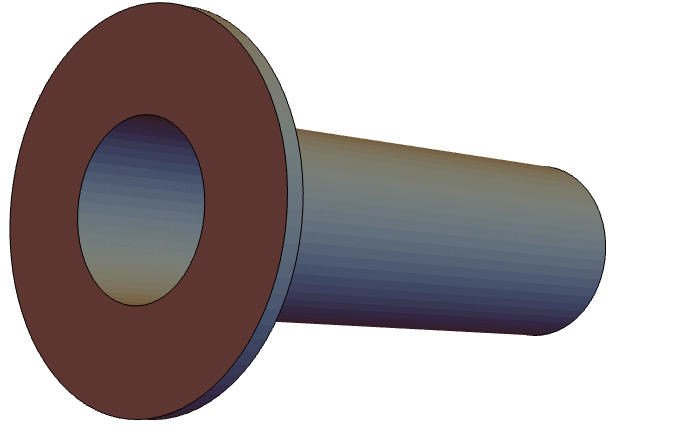
Since the geometry of the pipe and the boundary conditions are rotationally symmetric about the 
axis, an axisymmetric model can be used. The governing equation for describing the sound wave propagation is the axisymmetric Helmholtz equation.
Set up the variables and parameters:
https://wolfram.com/xid/0d2p3il2o6flb01aecoci6-j381qi
The axisymmetric geometry can be approximated by a 2D rectangle, which represents a cross-section of the pipe in the 
plane:
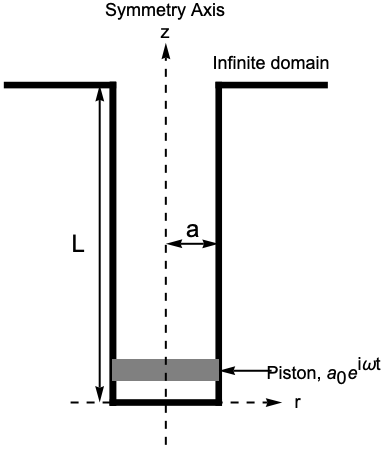
Set up the rectangle region with 
as the radius of the tube and 
as the length of the tube:
https://wolfram.com/xid/0d2p3il2o6flb01aecoci6-eilxud
In the model, there are two boundary conditions. One is a NeumannValue, which expresses the acceleration of the piston 
with 
:
https://wolfram.com/xid/0d2p3il2o6flb01aecoci6-fyxwc6
The second boundary condition is an AcousticImpedanceValue with impedance 
. The impedance 
is given by the following approximation, where 
is the wavenumber:
https://wolfram.com/xid/0d2p3il2o6flb01aecoci6-cbmz7h
https://wolfram.com/xid/0d2p3il2o6flb01aecoci6-d8gb18
Solve the PDE with 
with a MaxCellMeasure defined by 
and with a resolution of 12 to get an accurate result:
https://wolfram.com/xid/0d2p3il2o6flb01aecoci6-hvsgb
Visualize the pressure distribution in the full 3D region:
https://wolfram.com/xid/0d2p3il2o6flb01aecoci6-oljmh8
Wolfram Research (2020), AcousticPDEComponent, Wolfram Language function, https://reference.wolfram.com/language/ref/AcousticPDEComponent.html (updated 2023).Text
Wolfram Research (2020), AcousticPDEComponent, Wolfram Language function, https://reference.wolfram.com/language/ref/AcousticPDEComponent.html (updated 2023).
Wolfram Research (2020), AcousticPDEComponent, Wolfram Language function, https://reference.wolfram.com/language/ref/AcousticPDEComponent.html (updated 2023).CMS
Wolfram Language. 2020. "AcousticPDEComponent." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2023. https://reference.wolfram.com/language/ref/AcousticPDEComponent.html.
Wolfram Language. 2020. "AcousticPDEComponent." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2023. https://reference.wolfram.com/language/ref/AcousticPDEComponent.html.APA
Wolfram Language. (2020). AcousticPDEComponent. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/AcousticPDEComponent.html
Wolfram Language. (2020). AcousticPDEComponent. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/AcousticPDEComponent.htmlBibTeX
@misc{reference.wolfram_2025_acousticpdecomponent, author="Wolfram Research", title="{AcousticPDEComponent}", year="2023", howpublished="\url{https://reference.wolfram.com/language/ref/AcousticPDEComponent.html}", note=[Accessed: 26-March-2025
]}BibLaTeX
@online{reference.wolfram_2025_acousticpdecomponent, organization={Wolfram Research}, title={AcousticPDEComponent}, year={2023}, url={https://reference.wolfram.com/language/ref/AcousticPDEComponent.html}, note=[Accessed: 26-March-2025
]}