AcousticImpedanceValue[pred,vars,pars]
represents a time or frequency domain impedance boundary condition for PDEs with predicate pred indicating where it applies, with model variables vars and global parameters pars.
AcousticImpedanceValue[pred,vars,pars,lkey]
represents a time or frequency domain boundary condition with local parameters specified in pars[lkey].


AcousticImpedanceValue
AcousticImpedanceValue[pred,vars,pars]
represents a time or frequency domain impedance boundary condition for PDEs with predicate pred indicating where it applies, with model variables vars and global parameters pars.
AcousticImpedanceValue[pred,vars,pars,lkey]
represents a time or frequency domain boundary condition with local parameters specified in pars[lkey].
Details


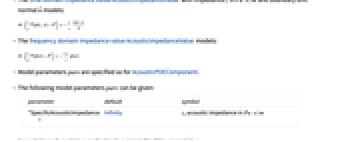
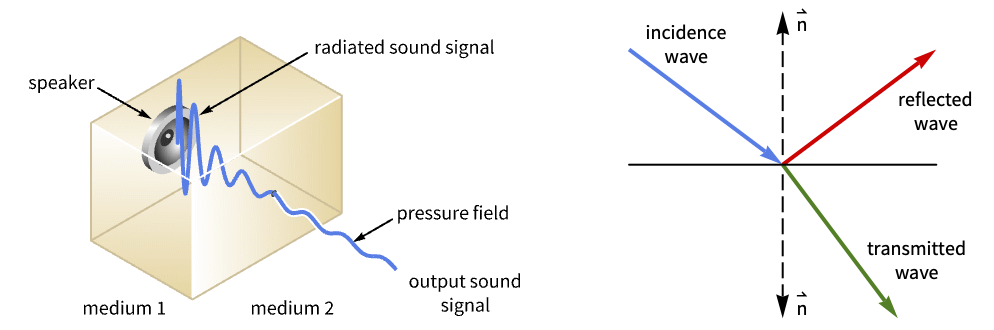
- AcousticImpedanceValue specifies a boundary condition for AcousticPDEComponent and is used as part of the modeling equation:
- AcousticImpedanceValue is typically used to model a boundary material that is partially transparent to sound.
- AcousticImpedanceValue models a time or frequency domain impedance with dependent variable pressure
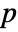 in
in 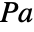 , independent variables
, independent variables 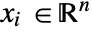 in
in 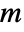 and time variable
and time variable 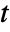 in
in 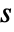 or frequency variable
or frequency variable 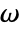 in
in 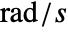 .
. - Time-dependent variables vars are vars={p[t,x1,…,xn],t,{x1,…,xn}}.
- Frequency-dependent variables vars are vars={p[x1,…,xn],ω,{x1,…,xn}}.
- The time domain acoustics model AcousticPDEComponent is based on a wave equation with time variable
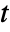 , density
, density 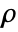 , sound speed
, sound speed 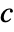 and sound sources
and sound sources 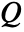 and
and 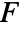 :
: - The frequency domain acoustics model AcousticPDEComponent is based on a Helmholtz equation with angular frequency
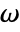 :
: - The time domain impedance value AcousticImpedanceValue with impedance
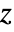 in
in 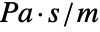 and boundary unit normal
and boundary unit normal 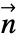 models:
models: - The frequency domain impedance value AcousticImpedanceValue models:
- Model parameters pars are specified as for AcousticPDEComponent.
- The following model parameters pars can be given:
-
parameter default symbol "SpecificAcousticImpedance" Infinity 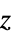 , acoustic impedance in
, acoustic impedance in 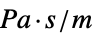
- AcousticImpedanceValue evaluates to a generalized NeumannValue.
- The boundary predicate pred can be specified as in NeumannValue.
- An impedance boundary can be used with:
-
analysis type applicable Time Domain Yes Frequency Domain Yes Eigenfrequency No - If the AcousticImpedanceValue depends on parameters
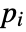 that are specified in the association pars as …,keypi…,pivi,…, the parameters
that are specified in the association pars as …,keypi…,pivi,…, the parameters 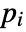 are replaced with
are replaced with 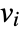 .
.
Examples
open all close allBasic Examples (5)
Set up a time domain acoustic impedance boundary:
Set up a frequency domain acoustic impedance boundary:
Set up a time-independent acoustic impedance boundary:
Define model variables vars for a transient acoustic pressure field with model parameters pars:
Define initial conditions ics of a right-going plane wave ![]() :
:
Set up the equation with an acoustic impedance boundary at the right and an impedance ![]() of
of ![]() :
:
Define model variables vars for a frequency domain acoustic pressure field with model parameters pars:
Set up the equation with a radiation boundary at the left, an acoustic impedance boundary at the right and an impedance ![]() of
of ![]() :
:
Visualize the solution in the frequency domain at various frequencies ![]() :
:
Scope (2)
Applications (1)
The following acoustic model describes an open pipe, wherein a vibrating piston is placed inside one end of the pipe while the other end of the pipe opens into an infinite domain. In this case, an impedance boundary condition is placed on one end to model the infinite domain. The pipe that will be modeled is a flanged circular pipe, as shown in the following figure below:
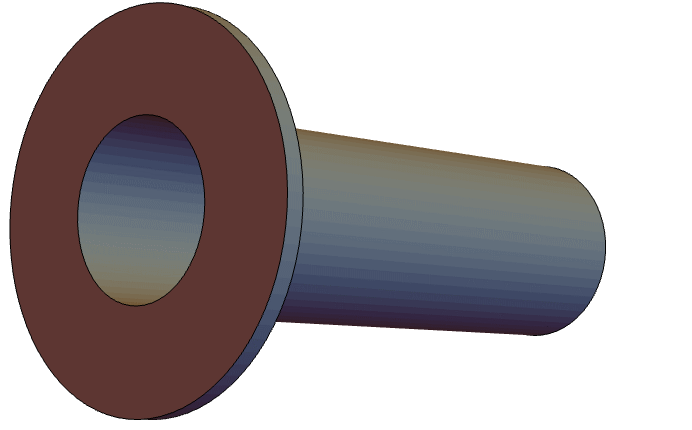
Since the geometry of the pipe and the boundary conditions are rotationally symmetric about the ![]() axis, an axisymmetric model can be used. The governing equation for describing the sound wave propagation is the axisymmetric Helmholtz equation.
axis, an axisymmetric model can be used. The governing equation for describing the sound wave propagation is the axisymmetric Helmholtz equation.
Set up the variables and parameters:
The axisymmetric geometry can be approximated by a 2D rectangle, which represents a cross-section of the pipe in the ![]() plane:
plane:
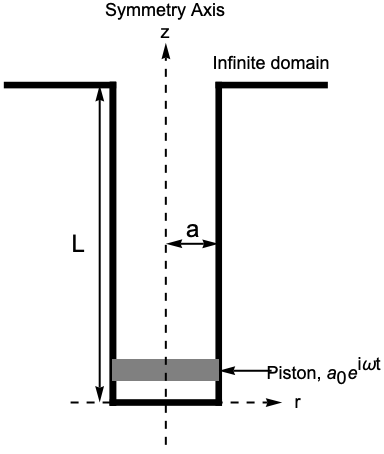
Set up the rectangle region with ![]() as the radius of the tube and
as the radius of the tube and ![]() as the length of the tube:
as the length of the tube:
In the model, there are two boundary conditions. One is a NeumannValue that expresses the acceleration of the piston ![]() with
with ![]() :
:
The second boundary condition is an AcousticImpedanceValue with impedance ![]() . The impedance
. The impedance ![]() is given by the following approximation, where
is given by the following approximation, where ![]() is the wavenumber:
is the wavenumber:
Solve the PDE with ![]() with a MaxCellMeasure defined by
with a MaxCellMeasure defined by ![]() and with a resolution of 12 to get an accurate result:
and with a resolution of 12 to get an accurate result:
Possible Issues (1)
The default value for "SpecificAcousticImpedance" is Infinity:
Tech Notes
Related Guides
History
Text
Wolfram Research (2020), AcousticImpedanceValue, Wolfram Language function, https://reference.wolfram.com/language/ref/AcousticImpedanceValue.html.
CMS
Wolfram Language. 2020. "AcousticImpedanceValue." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/AcousticImpedanceValue.html.
APA
Wolfram Language. (2020). AcousticImpedanceValue. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/AcousticImpedanceValue.html
BibTeX
@misc{reference.wolfram_2025_acousticimpedancevalue, author="Wolfram Research", title="{AcousticImpedanceValue}", year="2020", howpublished="\url{https://reference.wolfram.com/language/ref/AcousticImpedanceValue.html}", note=[Accessed: 09-March-2026]}
BibLaTeX
@online{reference.wolfram_2025_acousticimpedancevalue, organization={Wolfram Research}, title={AcousticImpedanceValue}, year={2020}, url={https://reference.wolfram.com/language/ref/AcousticImpedanceValue.html}, note=[Accessed: 09-March-2026]}