How Do You Like Your Boiled Eggs?
This application example of boiling an egg will demonstrate step by step how a computer simulation is created. It includes each stage of the process as the model is created, evaluated and refined to a satisfactory level. This example is chosen because most people have some experience with cooking an egg. The creation of this model is presented in various stages. Each version has additions that bring the simulation closer to modeling the process of boiling an egg.
There were two important points for the modeler to consider:
First, familiarity with the underlying physics helps with the selection of the type of model. The egg is taken from its storage and put in boiling water for a certain amount of time. Depending on the amount of time, the resulting contents of the egg may be runny, hard-boiled or something in between. The hot water changes the egg's consistency. The temperature evolution inside the egg can be calculated with the heat equation and modeled with a partial differential equation (PDE) model. Which equation to use to model a particular effect is something a modeler will learn from experience.
Second, the simulation result needs to be assessed. There are various ways to verify a simulation. In the case of boiling an egg, experimental data is readily available. Influenced by the size of the egg, the shell and other factors, an egg is boiled in four to eight minutes, depending on the desired consistency inside the egg. Access to experimental data is important, as the purpose of a model is to replicate some phenomena in a computer. Experimental data helps determine how well the replication worked compared to the real-world process.
There are other methods for verification, but they are slightly different in purpose. In some cases, analytical solutions to equations can be used, or a second software program is used to create and run a simulation to compare results with the first simulation. Examples of these types of verifications can be found, for the case of the heat equation, in the Heat Transfer Verification Tests notebook. Both of these cases assume that the equations used are appropriate for the specific example and that they capture the essential physics.
Another type of verification is to create a different type of model and see if the two models concur. For example, a System Modeler model could be created.
The most meaningful verification, however, is to verify against experimental data. Here is a list of egg cooking times and the resulting egg consistency:
To get started, the Finite Element package is loaded.
Setting the $HistoryLength to 0 means that Wolfram Mathematica will not save old output if it no longer needs it. This will save computational memory at a minimal cost in convenience.
Start very, very simple—Version 1
The purpose of this first model is to get a workflow started that is as simple as conceivably possible. The simulation does not have to deliver the final results immediately.
The first step is to create a geometry. As a start, a semi-disk is used for the geometry of the egg. This can and will be changed later. An axisymmetric geometry is used. This helps to keep things simple because creating a 2D geometry and mesh are simpler than creating a full 3D geometry. Also, a 2D simulation will finish much quicker than a 3D simulation. A simple geometry has the advantage that the finite element mesh that is created does not need as many elements to approximate the geometry, and thus the simulations run faster than in a 3D case. Fast evaluation is useful initially, because many things will need to be tried, and waiting a long time for a simulation to finish is not helpful.
An egg is about 5 [
] in diameter. To keep things simple, SI base units are used, and this means the radius of an egg is about 0.025 [
].
To start, this completely ignores the fact that the egg has an egg yolk and an egg white region.
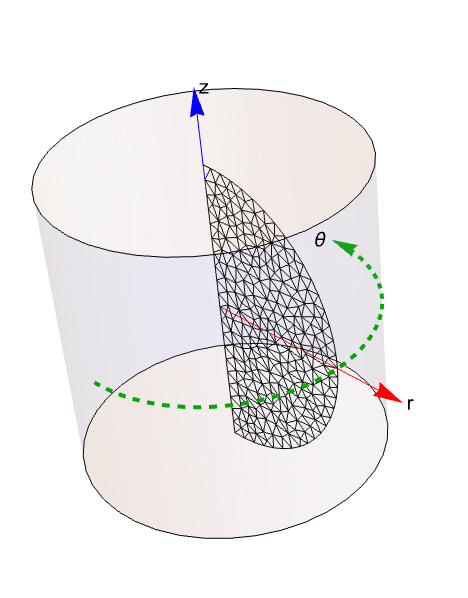
As mentioned above, the geometry and the PDE utilize an axisymmetric region geometry. The geometry and the differential equation can make use of truncated cylindrical coordinates. This is best visualized as follows:
Show the geometry and the mesh in a cylindrical setting, with a radial direction 
and a vertical direction 
. The azimuthal direction 
is truncated, and the heat distribution in that direction is assumed to be constant.
All quantiles involved will use SI base units, which means that the model units are in [
], the time unit is in [
], and the temperature unit is in [
].
Next, the partial differential equation model is set up. In this case, it is a heat transfer model. The equation will be set up with the HeatTransferPDEComponent function. This function needs variables vars and parameters pars. The first thing to do is think about the variables needed. The heating of the egg is a time-dependent process. Thus, we need a time variable 
[
]. The dependent variable for a heat transfer equation is the temperature 
[
]. Dependent variable refers to the variable for which a solution is being sought. The independent variables are the spatial variables 
and 
[
] in the radial and the vertical directions, respectively.
An introduction to the heat equation is given in the Heat Transfer monograph but is not necessary for this example.
Once the variables are set up, parameters need to be specified for the HeatTransferPDEComponent function. Since an axisymmetric model will be created, the RegionSymmetry is specified.
These definitions will lead HeatTransferPDEComponent to use default values for all quantities that it needs, which is sufficient for now but will be addressed again later.
HeatTransferPDEComponent created an axisymmetric partial differential operator in the dependent variable 
, the independent spatial variables 
and 
and the time variable 
.
Every PDE model needs boundary conditions. Boundary conditions specify the behavior of the PDE model outside of the simulation domain. Basically, boundary conditions specify how the world looks outside of the geometry. In this case, the boiling water is modeled with a temperature boundary condition of 100 [
] on the outside of the egg. Because the PDE model used is time dependent, initial conditions also need to be specified.
Initial conditions specify the state of the model at the beginning of the simulation time. The PDE will then take this initial state and move it forward in time, within the constraints of the boundary conditions. In this case, the assumption is that the egg taken from storage is at room temperature of 20 [
]. Since the units of the model are in SI base units, the temperatures are converted to [
].
The boiling water is modeled as a boundary condition. One might be tempted to directly set the outside temperature to 100 [
]. This, however, poses a problem. The initial condition at the boundary and the boundary condition are not consistent. The value of the initial condition at 
is set to 20 [
] everywhere, including the boundary. A boundary condition of 100 [
] contradicts this setting, since the boundary condition is also valid at 
. This is physically impossible, although it is common practice in finite element analysis, which does not make it more correct. The proper way to handle this is to start the system from rest. In essence, putting the egg into the boiling water is a process in itself that needs to be modeled. Here a function is used to ramp up the temperature at the boundary from the value of the initial condition to the boiling condition in a short amount of time.
The last question to answer concerning the boundary condition is where it is active. One way to do that is by using markers that are present in the mesh.
The boundary condition is applied at all positions where there are markers 2 or 3, or in this case, where the marker is not 1. This boundary condition is generated with the function HeatTemperatureCondition.
At 
, there is the axis of revolution, and a symmetry boundary condition is given by HeatSymmetryValue. This evaluates to a Neumann 0 value boundary condition. Since Neumann 0 boundary conditions are the default boundary condition if nothing is specified on some part of the boundary, the boundary value might as well be omitted. It is added in this version of the model but will be omitted in subsequent versions.
The last piece to set up is the simulation time. How long should the simulation run? Since for now the material parameters are ignored, they default to 1 unit. For this reason, a simulation time of 1 [
] is chosen. Again, this will be updated once the material parameters are set up.
The solution of the equation is then done by NDSolveValue.
The solution is returned as an InterpolatingFunction. This function can then, for example, be plotted. For now, the minimal and maximal values are extracted.
The initial temperature initT was set to 20 [
]. The maximal boundary condition is set to 100 [
]. Since there are no heat sources or sinks, the minimal and maximal temperatures must also be in the range from 20 [
] to 100 [
].
The values are approximately 20 [
] and 100 [
]. Some variations from the lower and upper bounds are expected. Because this is a numerical solution, it is not reasonable to expect perfect agreement. However, how much deviation is acceptable? This will be discussed later. In the meantime, these values are plausible.
Since this is a time-dependent simulation, it is common to animate the result. For this, the solution is visualized at various points in time, and then the frames are concatenated to form an animation.
When these frames are stored in the notebook, they can require significant storage space. For this reason, they are rasterized. For full visual fidelity, the following code section can be commented out.
At time 
, the animation shows the value of the initial condition, and then the domain is heated to the temperature of the boundary condition. This does not model the boiling of an egg but only serves to get a workflow established. When designing a PDE model, it is important to remember:
In the next version, material properties are added.
Add initial material parameters—Version 2
In this next version, the default material parameters are replaced by more specific values. Start from the general heat transfer equation given by:
The dependent variable in the heat equation is the temperature 
, which varies with time 
and position 
. The partial differential equation (PDE) model describes how thermal energy is transported over time in a medium with density 
and specific heat capacity 
. The specific heat capacity is a material property that specifies the amount of heat energy that is needed to raise the temperature of a substance with unit mass by one kelvin.
Besides the time derivative part, the PDE is made up of several components. First and foremost, there is a diffusive term: 
with a thermal conductivity 
.
The second part is a convective term: 
with a flow velocity 
for modeling internal heat convection. This term is only present if the medium allows for an internal flow. If the simulation medium is a solid, then this term is zero.
The term 
denotes a heat source within the domain and is explained in the Source Types section.
All material quantities may very well depend on the temperature 
. This will then result in a nonlinear heat equation.
The equation provided by HeatTransferPDEComponent is broadly applicable. The first step is to see which parts of it are needed.
In this model, the heat distribution strictly inside the egg is modeled. The model does not consider, for example, the fluid flow around the egg. As a consequence, there is no part where a heat convection is present. The convective term can be omitted from the equation:
The next aspect is internal heat generation, or an internal source 
. All the heat in the egg comes from the outside, through the boundary conditions. There is no internal heat source and thus 
, which leads to this equation:
The reference page of HeatTransferPDEComponent indicates that the following parameters should be specified:
The values used here are estimates of the average values for egg white and egg yolk. Once this workflow is established, more refined values for the two materials will be used.
Because more realistic material values are used than in Version 1, the simulation timespan also needs to be adjusted. For this, an intuitive value for the boiling time of an egg is used.
All other parameters remain the same in this step.
That is odd! The value suggests a minimal temperature below 0 [
]. Is this plausible? Absolutely not. The initial temperature was 20 [
], and the heating allowed a maximal temperature of 100 [
]. Since there is no other heat source or heat sink, it is physically not possible that the solution is outside of these temperature bounds. This leads to an important point:
You can see that there are wriggles just inside the boundary. A 3D plot of the solution surface shows this even better.
The plot of the solution reveals that there are undershoots close to the boundary. Zooming in and visualizing the finite element mesh at the same time reveals that the undershoots happen within a few elements layers close to the boundary.
Again, undershoots can be seen at the boundary. Where do they come from, and what can be done about them? To determine this, it is instructive to look at the solution on the axis of symmetry at 
and the mesh nodes that are on the axis. It would be equally instructive to look at any other line, such as 
. The point is to zoom into the solution a bit more.
0 to 0.1 in relation to the mesh coordinates in black:When the time slider is moved, the temperature increases at the left and right boundaries. Over- and undershoots, or oscillations, are seen almost immediately. What is causing this?
The distance between nodes at the boundary is about 1 [
]. At the same time, the rise of the temperature is 80 [
] in 
of a second [
]. The mesh cannot resolve these steep temperature gradients at the boundary. This results in physically wrong solutions, like temperature values below the initial temperature when there are no heat sinks. The reason is that the default quadratic shape functions cannot approximate the solution at the boundary. There are too few mesh elements to do that.
What can be done about the insufficiency of the resolution at the boundary? The finite element mesh needs to be able to represent the solution. The solution can be improved by refining the mesh. A brute force approach would be to refine the entire mesh, but that has the disadvantage that there will be many elements also within the domain where they are, until now, not needed and will require computational resources. A better way to deal with the situation is to refine the mesh near the boundary.
As a comparison to the above mean distance computation, the minimal edge length of the initial mesh can be estimated by taking the Sqrt of element areas.
In the next step, a mesh refinement function is created. The purpose of the function is to create a mesh that is refined at the boundary. This can be done by using a signed distance function. This gives a distance measure from anywhere within the domain to the boundary. Based on that, the MeshRefinementFunction will tell the mesh generation process how fine elements need to be in a specific area.
This new mesh has substantially more elements toward the boundary.
Next, the PDE is solved once more with the refined mesh. To monitor the progress of the time integration of the PDE, a Monitor has been added. The time integration will now take longer than previously because of the increase in the number of mesh elements.
The over- and undershoot are much better contained now. The remaining over- and undershoot can be further reduced by additional refinement of the mesh, but at this point the number of mesh elements and the solution quality seem to be in a reasonable balance.
The issue with the oscillation is resolved. It is time well spent trying to find a mesh that has just enough elements to resolve the physics adequately.
When looking at the solution, the temperature the egg boiling model produces seems too low for a given time.
With an internal temperature of only 42 [
] after 6 minutes of boiling, it is clear that the current model does not represent the boiling of an egg well.
Simulation models are based on simplifying assumptions. It is an art to determine which simplifications are admissible for a desired result quality. Several assumptions are made for this model:
The following sections will address some of these assumptions in order to improve the result.
Represent multiple material regions—Version 3
The next step is to take into account the two materials in an egg: the egg yolk and the egg white. A geometry is needed that differentiates the material regions.
Since there is now an internal material boundary, the boundary markers may have changed and need to be inspected.
The following material data is taken from [1].
In this solution, the temperature result of 38 [
] again seems too low for the given time. In fact, this temperature is even lower than the previous result 42 [
]. Therefore, the current model is not yet a good representation of boiling an egg.
Note the small kink in temperature at the material boundary of the egg yolk and white. This comes from the difference in the material properties.
Refine the model further—Version 4
The previous version suggested boiling times too long to match experience. A possible cause may be that the change in material coefficients is discontinuous and only happens after the denature temperature has been reached. In this new approach, a continuous change in the material coefficients will be used. For the density and conductivity, an interpolating function is created based on data from literature [2]. For the specific heat capacity, a different approach is used [1].
Next, the data is interpolated. This allows for querying the data in between data points and also extrapolating beyond the available data without giving a warning message.
Note that the argument of the interpolating functions is the temperature 
.
The same is done with the data for thermal conductivity.
Note that the argument of the interpolating functions is the temperature 
.
Next, the material data is used to set up the partial differential equation model:
Both the mass density and the thermal conductivity are now functions of temperature 
. At the same time, 
is the dependent variable for which a solution is sought. The fact that the coefficients are themselves temperature dependent makes the PDE nonlinear.
For the specific heat capacity values, a different approach is used [1]. Here an equation of the form 
is proposed, where 
is 51.8 for egg yolk and 88.2 for egg white. The coefficients 
, 
and 
are given, but in different units.
The partial differential equation has become nonlinear because the mass density and the thermal conductivity coefficients now depend on the temperature itself. As a result, the time to integrate the PDE increases. One way to alleviate this time increase is to use the non-refined mesh during the development stage and then use the refined mesh once satisfied with the setup of this stage. In this application example, the refined mesh is used.
Before looking at the solution, it is a good idea to track the denaturation of the egg yolk and egg white. This can be done by visualizing a contour in the solution domain that represents the denature temperature for the yolk and white [2].
In this model, you can observe that the dashed green line, the denaturation of the egg white, has reached the egg yolk region in about 6 minutes, which seems reasonable. One shortcoming of this model is that the denaturation of the egg yolk did not happen. Could this have to do with the geometry of the egg model?
Build a realistic egg geometry—Version 5
As a next step, the geometry of the egg is improved. A more realistic geometry can be created by using a spline for the outer boundary [3]. The yolk region is modeled through a circle.
The center of the egg yolk is shifted downward a bit to 
, and the radius of the yolk is also a bit smaller.
First, check that the markers remain the same.
The markers for the boundary condition remain the same.
The next step is to create a refinement function. For this, a helper geometry is created that is used in a signed distance function. This allows computation of the distance to the egg edge, which is used as a proxy for the amount of refinement. Since only the egg edge, but not the axis of symmetry, needs refinement, the helper geometry comprises both sides of the egg edge. This avoids computing a distance to the axis of symmetry.
Remember, the center of the egg yolk has been shifted downward to 
, and the radius of the egg yolk is smaller.
Use the model—Version 6
Once a model with satisfactory results has been established, the model can be used to make predictions. For example, in the original version, the initial egg temperature was set to a room temperature of 20 [
]. How does the boiling time change if the egg is taken from the refrigerator? In that case, the egg would have an initial temperature of about 8 [
].
To model this change in the condition of the egg, the initial temperature needs to be adjusted. As a consequence, the ramping up of the heat boundary condition needs adjustment.
The function that models the boundary condition temperature rise needs to be modified.
It turns out that a further refinement of the boundary layer in the mesh is necessary to achieve a result with a reasonable accuracy.
for the eggs starting from room and refrigerated initial temperatures and the corresponding denature positions:At 
[
], the difference in position of the denature line for the egg white (dashed green) is much larger than the difference for the egg yolk.
At 
[
], the egg white of the room-temperature egg has completely denatured, while the egg from the refrigerator still has some egg white that has not denatured.
Simulate periodic cooking of an egg—Version 7
Boiling an egg that results in a perfectly textured egg yolk and egg white, the albumen, can be a challenge for most cooks, since the yolk and albumen require two different temperatures to achieve the optimal texture for each. A new cooking method devised by food scientists, called periodic cooking, may offer a solution. Here we simulate the periodic cooking method. The egg is placed in boiling water at 100 [
] for two minutes, immersed in 30 [
] water for two minutes, then back to the boiling water to repeat the process multiple times, for a total of 30 minutes (1800 [
]).
The function that models the boundary condition temperature alteration needs to be modified.
Because the solution took longer to compute than previous models, it might make sense to save the computed solution for later work.
Some operating systems remove the content of $TemporaryDirectory after a restart.
With the periodic boiling of the egg, the denature positions move forward and back in the egg.
Also, in the cross section at 
, the temperature moves up and down in the egg. The dashed line is the radius of the egg yolk and the larger part of the temperature ups and downs is outside of the egg yolk radius. Inside the radius, the temperature also moves up and down but to a much lesser degree.
References
[1] J. Coimbra et al., "Density, Heat Capacity and Thermal Conductivity of Liquid Egg Products," Journal of Food Engineering, 74(2), 2006 pp. 186–190. https://doi.org/10.1016/j.jfoodeng.2005.01.043.
[2] B. Abbasnezhad et al., "Thermophysical and Rheological Properties of Liquid Egg White and Yolk during Thermal Pasteurization of Intact Eggs," Journal of Food Measurement and Characterization, 8(4), 2014a pp. 259–269. doi:10.1007/s11694-014-9183-6.
[3] V. N. Narushin et al., "Delineating an Ovoidal Egg Shape by Length and Breadth: A Novel Two-Parametric Mathematical Model," Biosystems Engineering, 224, 2022 pp. 336–345. https://doi.org/10.1016/j.biosystemseng.2022.11.003.
[4] E. Di Lorenzo, F. Romano, L. Ciriaco et al., "Periodic Cooking of Eggs," Communications Engineering 4(5) 2025. https://doi.org/10.1038/s44172-024-00334-w.