Hygroscopic Swelling

Hyperelastic material and multiphysics	References
Gasket application example

Solids can absorb water molecules in humid environment and this accumulation can cause the solid to swell and and result in increased stress and strain [1]. This phenomenon happens in several environment like industrial plants, naval applications and biological laboratories, and it must be modeled accurately to investigate its effects.

This swelling results in an inelastic strain that us proportional to difference between a concentration and a strain-free reference configuration:

Here represents the coefficient of hygroscopic swelling, is the moisture concentration and a moisture referencing value. The moisture concentration is typically described in [] and governed by the mass transport equation.

The water molecules absorption leads to two different types of effects on the solids, depending on the constraints. On free structures, it induces deformations, while on completely fixed structures it induces stresses. In real structures, generally only partially constrained, it leads to a mixture of effects.

In this application example we show how to model hygroscopic swelling combined with thermal expansion.

Load the finite element package:

Hyperelastic material and multiphysics

As introduced in the Hyperelasticity Monograph it is possible to couple several phenomena within a finite elasticity deformation process through a kinematic decomposition. The moisture-induced stress can be modeled similarly to the thermoelastic deformative process, and it is then possible also to couple both the effects.

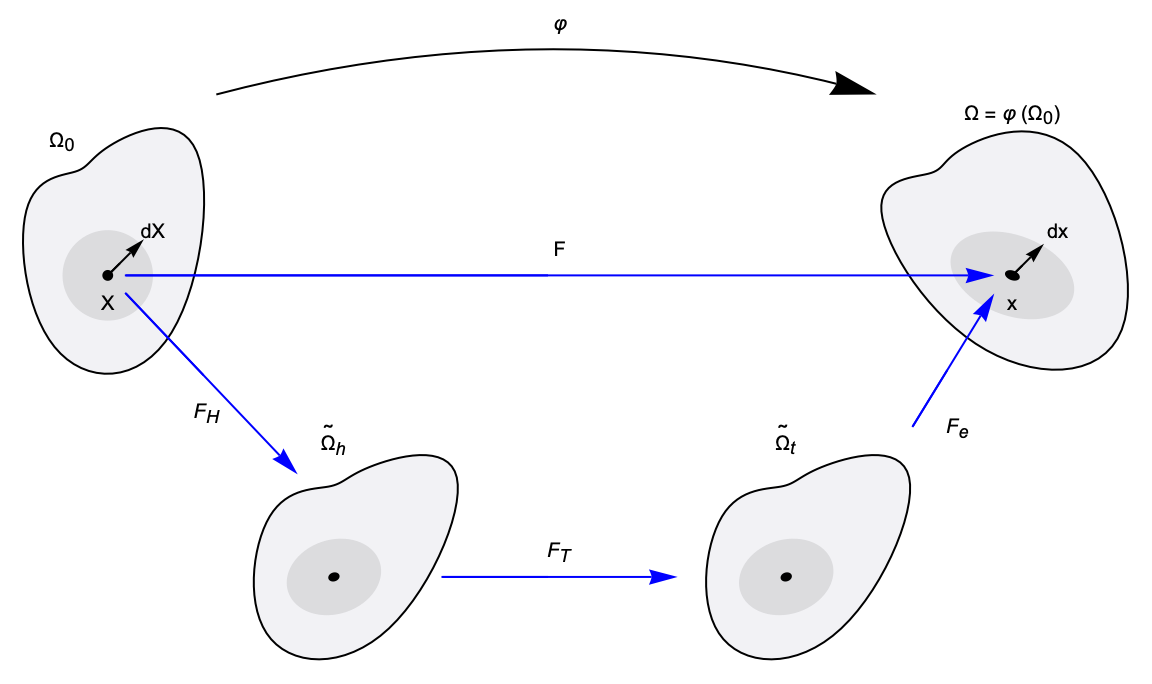
The kinematic approach starts splitting the deformation gradient into an elastic part and an inelastic part :

Where contains both the inelastic contribution due to the thermal inelastic deformation gradient and to the hygroscopic inelastic deformation gradient .

The thermal inelastic deformation gradient is introduced in the thermoelasticity section as:

The implementation of the ThermalInelasticDeformationGradient:

For the thermal inelastic deformation gradient we can make use of the build in thermal strain function.

The hygroscopic deformation gradient is referred to the moisture relative concentration through the coefficient of hygroscopic swelling as:

Since there is no predefined hygroscopic strain function, we write a small helper function to compute that.

The implementation of the HygroscopicInelasticDeformationGradient:

So, the total deformation gradient maps the reference configuration to the current configuration . However, for each intermediate configuration different phenomena are described. The current configuration include the mechanical problems described focusing on the elastic deformation gradient, defined as:

To set up the equilibrium equation the elastic Piola-Kirchhoff stress needs to be pulled-back to the reference configuration, to get a first Piola-Kirchhoff stress , accounting also for the inelastic contribution [3]. For more information, see the Hyperelasticity monograph.

The total deformation gradient maps the reference configuration to the current configuration . With a decomposition, two intermediate configurations are introduced. The hygroscopic inelastic deformation gradient maps to while thermal inelastic deformation gradient maps to . In the end, the elastic deformation gradient maps to .

Both the thermal and diffusive phenomena are described in their configuration. The mass transport phenomenon is represented in the intermediate configuration with the diffusion equation while the thermal process is represented in the configuration with the heat equation described in the following.

In addition, pull-back operations are needed to map the thermal and diffusive components to the reference configuration in order to solve the fully-coupled PDE in the reference configuration.

The hygroscopic inelastic deformation gradient map the reference configuration into the first intermediate configuration where the mass diffusion phenomenon is described. The stationary diffusion equation in solid domain reads:

Where represent the moisture concentration, , is the diffusion coefficient and denotes a mass production or consumption rate. For more information about the diffusion equation, see the Mass transport monograph.

In order to be solved together with the others PDE sets, the diffusion equation needs to be pulled-back to the reference configuration such that it is in the same reference frame. This requires to pull-back both the divergence and the gradient operators [2, pp 521], leading to:

Where is the hygroscopic inelastic deformation gradient and . As mentioned in the Hyperelasticity monograph for the thermo-elastic coupling, the Jacobian is in front of the divergence, which makes this equation not suitable for the finite element solver. More details are given in the section on The Coefficient Form of a PDE. We need to pull the inside the divergence and this can be done by adding a further term that compensates the effect that has inside the divergence. We can write:

This is in a proper coefficient from and the equation to implement is:

Similarly, also the heat equation needs to be pulled-back. This is described in the Hyperelasticity monograph and follows the same pull-back operation with the only difference that the deformation gradient, which leads to the second intermediate configuration, it is no more only the thermal inelastic one, but the complete inelastic deformation gradient, including both the thermal and hygroscopic ones, as described in eqn (1).

So the proper coefficient from and the equation to implement is:

In the following, an example is implemented to show the application of the coupling of the mechanical, thermal and moisture diffusion phenomena.

Gasket application example

Polymeric rubbers play a crucial role in the modern industrial landscape. These materials find applications across a wide range of sectors thanks to their unique properties such as resilience, high deformability and elastic response, resistance to chemicals and easiness in production. However, some of these materials may not respond so well to thermal load and/or a humid environment.

In the following example a gasket made from a rubber-like material is shown. The gasket fills a space in between two plates and it is used in an industrial oven working with mid-range temperature and a high moisture concentration. The plates are made in hydrophobic material which maintains a very low local moisture concentration. In addition, the plates are subjected to different temperatures. The upper one is also subjected to a vertical load which leads to a large deformation compared to the size of the gasket.

In addition to the main mechanical load, the material is subject to a humid environment with different temperature ranges. Plates at different temperature may induce a thermal deformation which can increase stress and strain. In addition, due to construction reasons of the system the internal region is filled with air with a very high content in moisture which may affect the hygroscopic deformation of the material.

A gasket made in from a rubber-like material shown in gray is subjected to vertical load . A cold plate , shown in blue, fixes the bottom side while the upper portion is loaded with a hot plate , shown in brown, representing both a mechanical load and a temperature boundary condition. The internal region is filled with air very rich in moisture, representing a moisture boundary condition shown in pink. Due to symmetry, the problem may be described representing only half domain.

Domain

The domain is symmetric, and it is sufficient to model half of the domain. To represent the mechanical symmetry condition the horizontal displacement of the midplane is fixed at while the vertical displacement is left free to move.

The bottom plate represents both a thermal and a mechanical boundary condition. It represents a cold temperature and fixes the vertical displacement of the rubber while a horizontal slide is allowed. In the contrary, the upper plate represents a hot surface with a mechanical load. In addition to that this plate is strongly glued with the gasket linking their displacements. For this reason, also the plate is represented, described as a very stiffer material compared to the rubber-like one.

The plate, due to construction requirements, is made of a hydrophobic material with a near to zero concentration in moisture while the internal boundary, shown in pink, has a very high moisture concentration .

Due to the different involved phenomena, the PDEs are expressed in function of displacements, temperature and concentration, all depending on spatial position.

Declare variables for the solid mechanics and heat transfer PDE:

The geometrical domain is represented by 11 boundary lines that connects 10 vertexes. Two different domains are identified by region markers, one for the deformable rubber and one for the stiffer plate. The generation and usage of ElementMarker is explained in the ElementMesh generation tutorial.

Define the geometrical dimensions:

Mesh the boundary:

Visualize the boundary mesh with node numbers:

Mesh the different domains:

Visualize the mesh with the different regions:

Material properties

Next, we define material properties. The material mechanics is described as a nearly-incompressible neoHookean hyperelastic behaviour.

Set up the neo Hookean model parameters for the rubber-like gasket material:

Set up the thermal parameters with a reference temperature of

[

Set up the diffusion parameters:

Mass transport

Before looking at the fully coupled PDE we will take a look at the hygroscopic absorption and how that can affect the mechanics and thus how to couple the physics.

As mentioned before, the dependent variable in the mass balance equation is the species concentration , which varies with position . The partial differential equation (PDE) model describes how chemical species are transported in a solid medium. First of all, an investigation of the diffusive process is performed.

Set up material parameters for the diffusion description:

Set up conditions representing boundaries of interest for BCs:

Set up boundary conditions for the internal domain:

Set up boundary conditions for the plates:

Solve the diffusion PDE:

Visualize the moisture concentration:

Due to the hydrophobic boundary condition on the plates and to the internal elevated concentration, the moisture spreads n the material thickness towards the right side.

In summary, by coupling the moisture diffusion with the induced strain in the mechanical model we expect a relatively high expansion on the internal side and less relevant effects near the plates.

Multiphysics

In order to investigate the effect of the moisture inside the material a fully coupled hygro-thermo-mechanical problem is shown next. First, the different phenomena are described and then the three coupled PDEs are solved together with a parametric solver allowing for gradually increasing the boundary conditions through a load multiplier .

Diffusion

The diffusion problem was described in the previous section, however the pull-back operation needs to be included to fully couple the phenomena. The internal boundary conditions is replaced introducing the load multiplier.

Set up material parameters for the diffusion description:

Set up boundary conditions for the internal domain:

As introduced in the eqn (2) the diffusion equation is written including the pull-back operation and a compensation term.

Set up the hygroscopic inelastic deformation gradient:

Set up the hygroscopic inelastic Jacobian and the transpose of the deformation gradient:

Set up the diffusion compensation term:

Set up the diffusion equation:

Set up the diffusion PDEs set:

Solid mechanics

In the mechanical description the equation representing the displacement and are introduced.

The mechanical description includes the vertical displacement constraint on the bottom side, the horizontal displacement constraint on the symmetry side and the vertical load on the upper plate. A nearly-incompressible neo-Hookean material model is used and the plate is represent as a very stiff material, with a material coefficient four orders of magnitude larger then that of the deformable rubber.

Set up material parameters for the mechanical description:

Specify the maximum load

Set up the traction boundary condition:

Set up the displacement condition on the bottom side:

Set up the displacement symmetry condition:

Set up the mechanical PDEs:

Thermal

The heat equation describing the temperature is then introduced as expressed in eqn (3) including the pull back operation and the compensation term. The boundary conditions on temperature are applied through the load multiplier .

Set up the temperature boundary condition:

Set up the thermal inelastic deformation gradient:

Set up the thermal inelastic Jacobian and the transpose of the deformation gradient:

Set up the total inelastic deformation gradient:

Set up the inelastic Jacobian and the transpose of the deformation gradient:

Set up material parameters for the thermal description:

Set up the compensation term:

Set up the steady-state heat equation:

Set up the mechanical PDEs set:

Solution

The final, coupled PDE involves the mechanical, the thermal and the diffusion components and so the solutions vector contains both the displacements u[x,y] and v[x,y], the temperature field and the concentration field.

Define global variables:

Now we set up the parametric solver. All the boundary load values are connected to the multiplier parameter .

Create a parametric function for the forced BCs with the parameter

Sometimes, it is needed to help NDSolve to figure out the ordering of the dependent variables. This is explained in more detail Finite Element Best Practice documentation.

The parametric function allows us to, step by step, slowly increase the multiplier from 0 to 1 and thus increasing the vertical force, the heat exchanges and the moisture concentration at the boundaries.

Set the maximum value for the multiplier:

Specify the number of step nsteps the initial solutions vector:

Monitor the progress of the solution while the load factor

is increased:

Extract the displacement results:

Extract the temperature results:

Extract the diffusion results:

Create the deformed mesh based on the computed displacement:

Visualize the deformed boundary of the entire domain in red and the undeformed in black:

Visualize the deformable part of the deformed object in red and the undeformed object in black:

Map the temperature field over the deformed mesh:

Visualize the temperature results:

Map the temperature field over the deformed mesh:

Visualize the moisture concentration:

Post processing

After obtaining the solutions it is interesting to investigate how the different involved phenomena affect stress and strain in the material.

The Green-Lagrange strain tensor represents the total strain. The total Cauchy-Green strain tensor contains, due to the multiplicative decomposition, both the contributions of the inelastic and elastic deformation processes.

Compute the total strain:

Visualize some components of the total strain:

We start from the expression of the total Green-Lagrange strain tensor :

Each Cauchy-Green strain tensor is computed starting from the corresponding deformation gradient and then the Green-Lagrange strain tensor is computed as indicated in the Hyperelasticity monograph.

Compute the inelastic Cauchy-Green strain tensor:

Compute the inelastic thermal Green-Lagrange strain tensor:

Next, we would like to compute the thermal strain . The inelastic thermal deformation gradient is defined as a function of the temperature and the load multiplier . These need to replaced with the actual values. Since the material is isotropic, it is sufficient to consider any one of the diagonal components of the thermal strain, as all diagonal components are the same.

Compute the thermal strain:

It is possible to replace the temperature results over both the undeformed or deformed mesh but the plot domain need to be selected accordingly. Since we replaced the deformedTemperature we have to plot over the deformedMesh.

Visualize the thermal strain:

It is possible to use the same approach for the hygroscopic strain computation.

Compute the inelastic Cauchy-Green strain tensor:

Compute the inelastic thermal Green-Lagrange strain tensor:

And we can compute the hygroscopic strain , replacing the moisture concentration and the load multiplier . Since the material is isotropic, it is sufficient to consider any one of the diagonal components of the thermal strain, as all diagonal components are the same.

Compute the thermal strain:

Visualize the thermal strain:

Then it is possible to compute the elastic Cauchy-Green by inverting the eqn (4) where the inelastic Cauchy-Green contains both the thermal and the hygroscopic contribution.

Replace the parameters in the inelastic Cauchy-Green strain tensor:

To compute the total Cauchy-Green strain tensor we solve for and obtain:

Compute the total Cauchy-Green strain tensor

Compute the elastic Cauchy-Green strain tensor

Compute the elastic Green-Lagrange strain tensor

Visualize some components of the elastic strain

In the end, we can investigate how the overall deformation results in the stresses inside the material.

Compute the Cauchy stress:

In some cases the symbolic expression in the stress tensor are so complicated that SymmetrizedArray can not figure out if the array is symmetric or not. In such a case we can force the symmetry of the stress tensor.

Symmetrize the Cauchy stress:

Compute the von Mises stress:

Next, when we replace the multiplier , the temperature and the moisture concentration . The expression is no longer a simple interpolating function but a compound expression which we evaluate on the undeformed mesh to construct a single interpolating function.

Replace results for the von Mises stress and construct an interpolating function:

Map the von Mises stress over the deformed mesh:

Visualize the von Mises stress in [kPa] over the deformable region:

References

1. Weitsman, Y. J. Effects of Fluids on Polymeric Composites; Comprehensive Composite Materials. 2000. https://doi.org/10.1016/B0-08-042993-9/00068-1.

2. Yosibash, Z. Weiss, D. Hartmann, S. (2014). High-order FEMs for thermo-hyperelasticity at finite strains. Computers and Mathematics with Applications, vol 67, pp. 477-496, https://doi.org/10.1016/j.camwa.2013.11.003

3. Wriggers, P. Nonlinear finite element methods; Springer 2008

Top