Radial Effects in a Tubular Reactor

Introduction	Visualization
1 Dimensional Adiabatic Plug Flow	Nomenclature
Extending the model	References

Introduction

Chemical reactors are at the core of chemical engineering processes. It is in these reactors that chemical reactions are made to take place. Chemical engineers are concerned about the design of the reactors seen that the desired output product should be produced with high efficiency.

In addition to continuous-stirred tank reactors and batch reactors, tubular reactors are also commonly used in the industry. Tubular reactors are made up of a cylindrical pipe. In the reactor, a variety of reactions can occur and many approaches can be taken in modeling a tubular reactor.

One aspect to consider when modeling tubular reactors is the flow profile in the reactor. Traditionally, to keep things simple, a plug-flow was assumed. A plug-flow assumes a constant velocity through the cross section of the tubular reactor. In an adiabatic case this has the benefit that no radial contributions, for example temperature, need to be considered and a 1D model is sufficient in this case.

In this notebook first a simple 1D plug flow based model is shown and then a more elaborate 2D model will be presented.

While tubular reactors are typically used for gas phase reactions, liquid phase reactors are not uncommon either. This example will consider a liquid phase reactor.

In this tubular reactor a liquid phase, exothermic and irreversible reaction will take place first in a plug flow regime and then in a laminar flow regime. The reaction taking place inside the reactor is a hydrolysis reaction between propylene oxide product , and water product to form propylene glycol, product . This process can take place at room temperature when catalyzed by sulfuric acid. This kind of reaction is exothermic which can be approximated as a first-order reaction given that the reaction takes place in an excess of water [Fogler, 2016]. First-order reactions are reactions that entirely depend on the concentration, such that by doubling the concentration the product is also doubled.

Show the chemical reaction:

This notebook illustrates how to model an exothermic reaction in a tubular reactor and see the concentration of the species and the temperature distribution in the domain.

Load the finite element package:

1 Dimensional Adiabatic Plug Flow

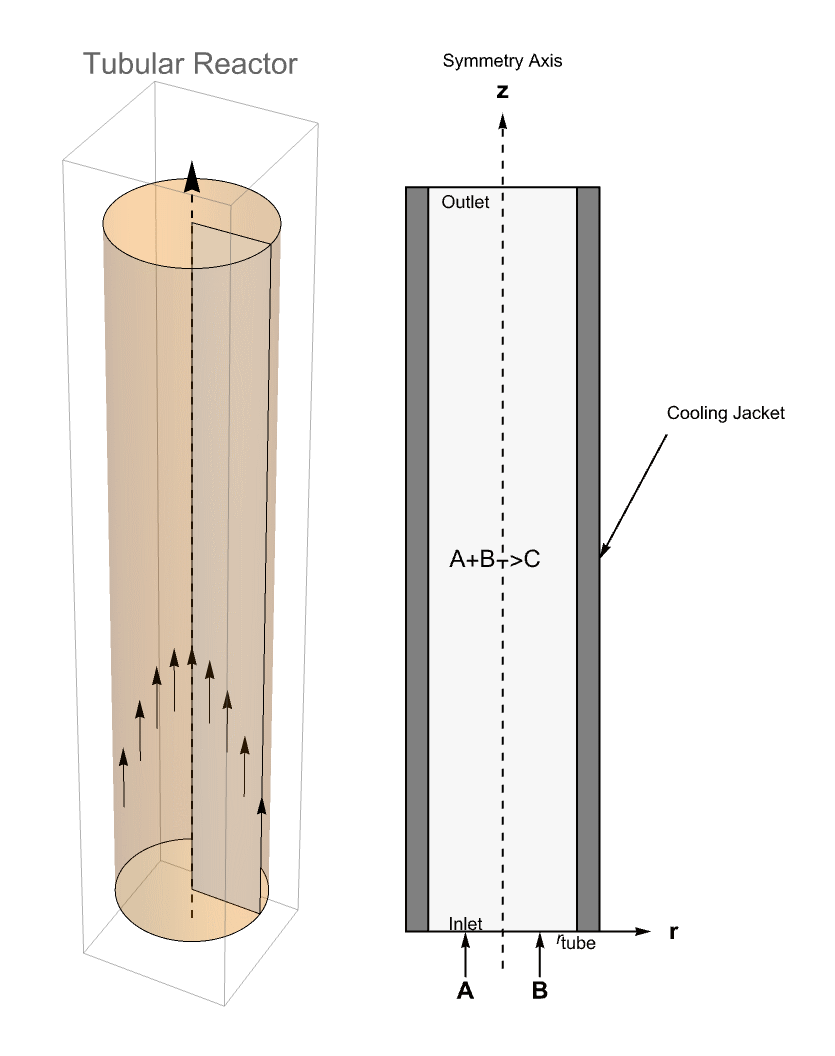
A schematic of a classical tubular reactor model with a plug flow profile and reactants A and B and resultant C is shown. The rector is oriented along the -axis.

In this first example a plug flow is assumed. It is also assumed that the system is adiabatic. Assuming an adiabatic system means that no energy is flowing into or out of the system, say, through a cooling mechanism. These assumptions allow to neglect all radial effects. As a consequence the model will be 1D.

Multiphysics Model Setup

Since this problem considers more than one physics domain, a multiphysics model is to be constructed. As a first step, the contributing physics domains are looked at independently. A heat transfer model and a mass transport model are set up to solve for the temperature field and concentration field within the reactor.

Initially, the flow field velocity within the reactor will be approximated by a plug-flow velocity profile in the -direction given by the following equation that represents the average velocity:

where is the total flow rate and is the radius of the reactor.

As a first step a 1D steady-state heat transfer and a mass transport model are defined.

Heat Transfer Model

The heat equation is used to solve for the temperature field in a heat transfer model:

where is the mass density in , is the specific heat capacity in , is the flow velocity in , is the thermal conductivity in , and is the heat source in .

Since the reaction is an exothermic process, the heat generated by the reaction is modeled by a heat source , which depends on both the chemical reaction rate, , and the heat of reaction, :

Set up a 1D steady-state heat transfer model:

Mass Transport Model

For a steady-state mass transport model the concentration field within the reactor is described by the following equation.

where denote the diffusion coefficient in , is the flow velocity, and is the reaction rate.

The chemical reaction rate depends on both the reactant concentration and the reaction rate constant, .

Note that for consumption reactions the reaction rate, , is negative.

The rate of reaction is temperature dependent according to the Arrhenius equation:

where is a frequency factor in , the activation energy in [J/mol], and the gas constant in .

Note that the standard notation of the reaction constant is denoted by , however, to avoid the conflict with thermal conductivity in this case, the non-standard symbol is used instead.

Set up a 1D steady-state mass transport model:

Parameters

Model variables

Besides the concentration variable , which gives us the concentration of the species , the conversion of species and the concentration of species can also be computed.

The conversion ratio of species

is given by:

Define the concentration of species

Material Parameters

The feed into the reactor consists of two streams. One stream is an equivolumetric mixture of propylene oxide and methanol, and the other stream is water containing 0.1 wt% (weight percent) of sulfuric acid. The molar flow rate of propylene oxide fed to the tubular reactor is 0.1 . The water is fed at a volumetric rate 3.5 times larger than the propylene oxide-methanol feed [Fogler, 2016].

To solve any of the proposed multiphysics models, material properties of the reactants and the mixture need to be specified.

First the density , heat capacity and molar weight are defined for each of the species.

Set up the material properties of Propylene Oxide using

as abbreviation:

Set up the material properties of Methanol using

as abbreviation:

Set up the material properties of the fluid medium water:

Set up the frequency factor

, the activation energy

, and the heat of reaction

for Propylene Oxide:

Set up the volumetric flow ratio:

Set up the molar

and volumetric flow rate

at the inlet:

Set up the total flow rate:

Set up the concentrations at the inlet:

Set up the thermal conductivity and the diffusion coefficient of the mixture using

as abbreviation:

Set up the gas constant

The density of the solution is defined as the weight sum using the initial concentrations of the species:

The heat capacity of the solution is defined as the weight sum using the concentration of

and

as a variable:

Set up the average velocity:

For further computation the magnitudes of the concentrations are extracted:

Model parameters

Specify the multiphysics model parameters.

Set up the reaction rate

and the heat source term

Set up the parameters to use:

Domain

The domain can be represented as a line that goes through the main axis of the tubular reactor from 0 to .

Specify the parameters of the geometry:

Create a 1D mesh of a Line primitive:

Boundary Conditions

Both, the temperature and the concentration are known at the inlet boundary .

Set up the MassConcentrationCondition at

Set up the HeatTemperatureCondition boundary condition at

Solve the PDE Model

In the following section, the fully coupled multiphysics model will be solved.

Specify the multiphysics PDE with the model parameters.

The PDE model presented here is nonlinear. To solve nonlinear PDEs the solver needs an initial seed for the solver. The default initial seed is 0 for every dependent variable. Now, since the model uses a reaction rate that has a expression in it, a 0 initial seed for the temperature is not possible. The remedy for this is easy. Here the initial seed values are set as . This assumes there is no concentration of and the temperature of the reactor is that of the inlet.

Solve the 1D coupled PDE model and monitor the total time and memory used.

Verify that there are no radial effects.

Visualize the temperature distribution:

Visualize the temperature changes at the inlet, middle section, and outlet:

Extending the model

The second tubular reactor model presented here will additionally have a cooling jacket surrounding the reactor. The cooling jacket will introduce radial effects as the temperature varies from the cooling jacket to the center of the reactor. Since the concentration is also linked to the temperature the concentration will also see a radial effect.

To consider radial effects it is necessary to make use of a 2D model using cylindrical coordinates . This can be done because the model is rotationally symmetric about the -axis, so the cylindrical coordinate variable disappears.

Since radial effects will be present due to the cooling jacket a laminar flow profile can also be considered. The radial effects are actually further increased if a laminar flow profile is present. That is because a laminar flow field has a parabolic form. Considering the cooling jacket at the wall and a low flow velocity at the wall compared to the center of the cylinder the laminar flow profile will increase the radial effects. The model shown is based on [Fogler, 2016] and is usually known as a Non-adiabatic laminar flow model.