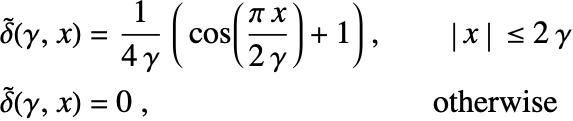PDEModels Best Practice
Conservative versus Non-conservative Convection
Generally speaking, a convection can be modeled in conservative and non-conservative forms. The conservative form is expressed as a ConservativeConvectionPDETerm and models ![]() . The alternative is to use a ConvectionPDETerm, which models
. The alternative is to use a ConvectionPDETerm, which models ![]() . Note the different positions of
. Note the different positions of ![]() .
.
Differences in Scale Spoil Numerical Solutions
When numerically solving differential equation models, it is important to pay attention to the scale of the components in the model and their relative and absolute sizes. For example, large differences in the scale of the geometry and the material parameters can spoil the solution. Also, the absolute size of a geometry compared to machine epsilon can have a bad effect on the accuracy of a solution. The main concern is that when this happens, there will most likely not be any warning message and the modeler will have to take this effect into consideration.
To explore this effect, take, for instance, a quantum well with a width ![]() and a confinement potential denoted as
and a confinement potential denoted as ![]() . Here, the Schrödinger equation will be solved and the first few bound eigenstates found.
. Here, the Schrödinger equation will be solved and the first few bound eigenstates found.
Here, ![]() represents the mass of the particle and
represents the mass of the particle and ![]() is the reduced Planck constant. It is important to realize that the parameters are specified in "SIBase" units. The length units are thus "Meters". At the same time, the well's length is only
is the reduced Planck constant. It is important to realize that the parameters are specified in "SIBase" units. The length units are thus "Meters". At the same time, the well's length is only ![]() "Angstroms", which means that the domain's dimensions are on the scale of
"Angstroms", which means that the domain's dimensions are on the scale of ![]() "Meters". Also, the "SIBase" units for the reduced Planck constant are "Kilograms" "Meters"^2 /"Seconds". This means that Planck's reduced constant has length units in the order of
"Meters". Also, the "SIBase" units for the reduced Planck constant are "Kilograms" "Meters"^2 /"Seconds". This means that Planck's reduced constant has length units in the order of ![]() "Meters".
"Meters".
This means the domain's length dimensions differ by several orders of magnitude from the correspondent model parameters' length dimensions and are also small compared to $MachineEpsilon.
Now proceed with the numerical calculation.
When establishing this problem's boundary conditions, keep in mind that, from a physics perspective, the wavefunction needs to decay to zero as the distance from the well approaches infinity. But numerically, defining an infinite domain is not possible, so a large enough domain is heuristically chosen, and later a Dirichlet condition is defined such that ![]() at the outer boundary. In this particular problem, a distance of four times the length of the well is deemed reasonable for the decay of the wavefunction.
at the outer boundary. In this particular problem, a distance of four times the length of the well is deemed reasonable for the decay of the wavefunction.
Note that the scale of the operator's coefficients is 10-20 and 10-39, which is much smaller than machine epsilon.
When looking at the eigenvalues vals, note that they are also smaller than machine epsilon. This is an indication that the solution might not be correct.
Now, explore the obtained eigenvalues and eigenfunctions.
In the plot above, at first glance, only the probability density of the first state, with energy ![]() , seems to resemble the functional form one would expect in the quantum well's ground state. Regardless of that, the other two probability densities do not have the expected shape.
, seems to resemble the functional form one would expect in the quantum well's ground state. Regardless of that, the other two probability densities do not have the expected shape.
Unfortunately, noting this requires experience. At this point, it is important to realize that it is always good practice to crosscheck a simulation result, either by using an analytical result, if available, or by using another numerical method. In this case, an analytical solution exists. The analytical solutions are defined in a section below, as their specifics are not relevant here. Also, the process does not change if a second numerical result is available in place of an analytical result.
Is clear that none of the obtained numerical eigenvalues are acceptable, based on the error percentage relative to the analytical eigenvalues. In particular, the second and third eigenvalues are further away from their analytical counterpart, compared with the first state. This can be more easily visualized in a plot.
The way to avoid all these issues is by properly scaling the geometry and the coefficients so that they are better aligned. That is done by redefining the length of the well to the scale of
instead of the previous "Meters".Also, since the dimensions of the geometry have changed, the PDE operator and boundary condition need to be redefined. First of all, the parameter "SchrodingerPotential" needs to be updated, since the length of the well was redefined. Moreover, given that the SchrodingerPDEComponent uses "SIBase" units by default, the unit for length is "Meters". Then, to redefine the PDE operator accordingly, the "ScaleUnits" parameter is used. In this case, "ScaleUnits"->{"Meters"->"Angstroms"} will result in all the length units in the physical parameters being rescaled to "Angstroms" and in turn provides the needed redefined PDE operator.
Note how now the coefficients' scale is of order 1 and 10.
Having done that, the problem can now be solved as usual.
Since the length units in the physical parameters have changed from "Meters" to "Angstroms", the obtained eigenstates will have units accordingly. In particular, for energy eigenvalues, the correspondent "SIBase" energy units are assigned, with the exception of substituting "Meters" for "Angstroms" before converting the eigenvalues into the desired energy unit, "Millielectronvolts" in this case.
Is important to note that since the units of the geometry are angstroms, the units of the wavefunction are ![]() , instead of the usual
, instead of the usual ![]() . This should be taken into account if the modeler wants to do posterior calculations with the wavefunctions.
. This should be taken into account if the modeler wants to do posterior calculations with the wavefunctions.
On the same note, to compare the probability densities with the analytical solution, the difference in units has to be taken into account. The units of the analytical wavefunction are ![]() . For that reason, the analytical probability density output and the independent variable are scaled down by a factor of
. For that reason, the analytical probability density output and the independent variable are scaled down by a factor of ![]() .
.
It is now evident that the probability densities exhibit the anticipated functional form for the initial three bound states confined in a quantum well. Additionally, the numerical values of the energy levels closely match their analytical counterparts.
Analytical Solution
Rationalize has been used to get exact coefficients in the equation with a tolerance of one-tenth of the length of the well.
Discontinuity of Secondary Unknown Quantities
Sometimes, it is necessary to compute secondary quantities from the primary unknown variable. These secondary quantities are often proportional to the first derivative of the primary unknown variable. Unlike the primary unknown variable, secondary variables can become discontinuous across element boundaries.
The following example shows discontinuities that arise when taking the derivative of a dependent variable ![]() . Also, it shows how the secondary quantity
. Also, it shows how the secondary quantity ![]() becomes more accurate as the number of elements increases.
becomes more accurate as the number of elements increases.
The equation to solve is a diffusion term, with coefficient ![]() and a source term that varies quadratically in space. The equation is solved in a 1D domain from
and a source term that varies quadratically in space. The equation is solved in a 1D domain from ![]() to
to ![]() . For this problem, an analytical solution exists.
. For this problem, an analytical solution exists.
The source term is represented by the following equation:
where ![]() is a constant and
is a constant and ![]() is the independent variable.
is the independent variable.
Three different meshes will be used. The first will have two line elements, the second four and the last one 20.
A DirichletCondition will be specified at each end of the line. At the left, a value of 1 will be specified, and at the right, a value of 0.
This problem has an analytical solution, given below. Note that the solution is of fourth order. This means that the quadratic elements used in the interpolating function cannot perfectly interpolate the solution.
Note that in the primary quantity, the solution is more accurate when using more elements.
The interpolating function of the solution is quadratic. Now, when the derivative of the solution is computed, the quadratic interpolating function effectively becomes linear. Additionally, it is in the nature of the finite elements that the linear elements will introduce discontinuity at the element boundaries. However, these discontinuities can be reduced by refining the mesh, as will be shown next.
One can see a discontinuity at the intersection of each element, but the discontinuities are less pronounced than in the first case.
With 20 elements, the discontinuities effectively disappear.
Dirac Delta Functions
Regularized delta functions are used to implement monopole sources in various fields of physics, such as acoustics.
To make use of a monopole source, the monopole source is located at ![]() . Then the monopole source term
. Then the monopole source term ![]() may be written as:
may be written as:
where ![]() is a Dirac delta function at the source location
is a Dirac delta function at the source location ![]() .
.
The Dirac delta function, however, poses a problem in numerical simulations, as it cannot be resolved in the discretized spatial domain. This is because the Dirac delta function is singular at the source location ![]() . Hence, an approximation to the Dirac delta function is needed. The process of approximating the Dirac delta function is called regularization.
. Hence, an approximation to the Dirac delta function is needed. The process of approximating the Dirac delta function is called regularization.
There are various regularized delta functions ![]() available, for example:
available, for example:
where ![]() is the regularization parameter that controls the support of the regularized delta functions
is the regularization parameter that controls the support of the regularized delta functions ![]() . Typically,
. Typically, ![]() should have a size comparable to the mesh spacing
should have a size comparable to the mesh spacing ![]() .
.
Modifying ![]() will change the width of the regularized delta function; however, for
will change the width of the regularized delta function; however, for ![]() the spatial integral is always 1.
the spatial integral is always 1.
Over- and undershoots in Solutions
Sometimes over- and undershoots, or oscillations, can be seen in finite element solutions. Here is an example from a time dependent heat transfer. But the problem of the over- and undershoots can come up in any domain and it need not be a time dependent simulation either.
Because this is a time dependent simulation an initial condition is needed besides the boundary conditions. As an initial condition the geometry is set to be at a temperature of 293.15 [![]() ].
].
At both ends of the geometry a temperature of 373.15 [![]() ] is to be set. That is an 80 degree difference. Now, since the initial condition at both ends is at 293.15 [
] is to be set. That is an 80 degree difference. Now, since the initial condition at both ends is at 293.15 [![]() ] it is inconsistent with the boundary condition. The way to address this is to ramp up the boundary temperature with time.
] it is inconsistent with the boundary condition. The way to address this is to ramp up the boundary temperature with time.
With this setup it can be expected that the solution temperature is above the initial and the below the boundary temperature.
This is a surprise! Note, that the minimal temperature is below the initial temperature even though there are no heat sinks in the equation. Something is not right.
It is instructive to have a look at the solution together with the coordinates of the finite element mesh.
The reason for this undershoot is that the change in temperature at the boundary is happening very quickly and the steep gradient can not be resolved sufficiently well by the used mesh. A remedy is to use a mesh that is refined at the boundary.
Using the graded mesh substantially improved the undershoot. Using more elements or a different grading will further reduce the undershoot to a point where the numerical accuracy is satisfactory.
A further example of this can be seen in the Boiling an Egg application example.
Smoothed Step Functions
In some examples, a smoothed step function ![]() is used to prescribe a time profile for a transient parameter, for example, the heat flux
is used to prescribe a time profile for a transient parameter, for example, the heat flux ![]() or the surface temperature
or the surface temperature ![]() . The smoothed step function is defined as follows:
. The smoothed step function is defined as follows:
Here the minimum value and the maximum value the function ![]() can reach are denoted by
can reach are denoted by ![]() and
and ![]() . The location of the step is controlled by
. The location of the step is controlled by ![]() , and the smoothed steepness is controlled by
, and the smoothed steepness is controlled by ![]() .
.
Solving Memory-Intensive PDEs
The finite element method documentation has a section on Solving Memory-Intensive PDEs that may also be useful to know about in the context of PDE solving.
Units
Geometry Units
The units of a geometry can be rescaled. This is explained in the ElementMesh Generation tutorial.
Material Units
If the units of the geometry are different from the material units, then the material units can be scaled.
Internally, all material data units are converted to "SIBase" units. As a consequence, the default unit of length is "Meters". If the units of the geometry are also in meters, then nothing needs to be changed. If the units of the geometry are not in meters, then either the PDE and material properties need to be scaled to the units of the geometry or the geometry needs to be scaled to "Meters". To scale the units of the PDE and material parameters, the parameter "ScaleUnits" can be given. If not explicitly stated otherwise, examples in this notebook use the default "SIBase" units.
The procedure works in the same way when the material parameters are given as a Quantity.