gives the minimum positive arbitrary‐precision number that can be represented on a particular computer system.


$MinNumber
gives the minimum positive arbitrary‐precision number that can be represented on a particular computer system.
Details
- A typical value for $MinNumber is around
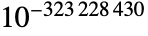 .
. - $MinNumber is an approximation given to $MachinePrecision and does not include all bits of the minimum representable number.
Examples
open all close allBasic Examples (2)
Properties & Relations (3)
$MinNumber has the smallest possible exponent:
$MinNumber×$MaxNumber is approximately 1:
$MinNumber is not a machine number:
It does have precision equivalent to that of machine numbers:
See Also
Tech Notes
Related Guides
History
Introduced in 1996 (3.0)
Text
Wolfram Research (1996), $MinNumber, Wolfram Language function, https://reference.wolfram.com/language/ref/$MinNumber.html.
CMS
Wolfram Language. 1996. "$MinNumber." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/$MinNumber.html.
APA
Wolfram Language. (1996). $MinNumber. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/$MinNumber.html
BibTeX
@misc{reference.wolfram_2025_$minnumber, author="Wolfram Research", title="{$MinNumber}", year="1996", howpublished="\url{https://reference.wolfram.com/language/ref/$MinNumber.html}", note=[Accessed: 06-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_$minnumber, organization={Wolfram Research}, title={$MinNumber}, year={1996}, url={https://reference.wolfram.com/language/ref/$MinNumber.html}, note=[Accessed: 06-January-2026]}