AcousticImpedanceValue
AcousticImpedanceValue[pred,vars,pars]
偏微分方程式についての時間領域あるいは周波数領域のインピーダンス境界条件を,適用される場所を表す述語 pred,モデル変数 vars,大域パラメータ pars で表す.
AcousticImpedanceValue[pred,vars,pars,lkey]
時間または周波数の領域境界条件を pars[lkey]で指定される局所パラメータで表す.
詳細



- AcousticImpedanceValueはAcousticPDEComponentの境界条件を指定し,以下のモデリング方程式の一部として使われる.
- AcousticImpedanceValueは,音に対して部分的に透過的な境界素材のモデル化によく使われる.
- AcousticImpedanceValueは時間あるいは周波数の領域インピーダンスを,従属変数圧力
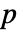 (単位:
(単位: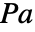 ),独立変数
),独立変数  (単位:
(単位: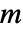 ),時間変数
),時間変数 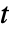 (単位:
(単位: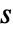 )あるいは周波数変数
)あるいは周波数変数 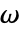 (単位:
(単位: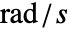 )でモデル化する.
)でモデル化する. - 時間依存モデル変数 vars は vars={p[t,x1,…,xn],t,{x1,…,xn}}である.
- 周波数依存モデル変数 vars は vars={p[x1,…,xn],ω,{x1,…,xn}}である.
- 時間領域音響モデルのAcousticPDEComponentは,時間変数
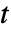 ,密度
,密度 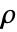 ,音速
,音速  ,音源
,音源  および
および  の波動方程式に基づいている.
の波動方程式に基づいている. - 周波数領域音響学モデルAcousticPDEComponentは,角周波数
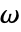 のヘルムホルツ(Helmholtz)方程式に基づいている.
のヘルムホルツ(Helmholtz)方程式に基づいている. - 時間領域インピーダンスの値AcousticImpedanceValueは,インピーダンス
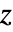 (単位:
(単位: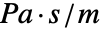 )で境界単位法線
)で境界単位法線 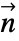 のモデル化する.
のモデル化する. - 周波数領域インピーダンスの値 AcousticImpedanceValueは以下をモデル化する.
- モデルパラメータ pars はAcousticPDEComponentと同じように設定される.
- 以下のモデルパラメータ pars が使用できる.
-
パラメータ デフォルト シンボル "SpecificAcousticImpedance" Infinity 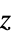 ,音響インピーダンス(単位:
,音響インピーダンス(単位: )
) - AcousticImpedanceValueを評価すると一般化されたNeumannValueになる.
- 境界述語 pred はNeumannValueにおけるのと同じように指定できる.
- インピーダンス境界は以下とともに使うことができる.
-
分析タイプ 適用可能性 時間領域 可能 周波数領域 可能 固有振動数 不可能 - AcousticImpedanceValueが連想 pars で…,keypi…,pivi,…]として指定されるパラメータ
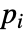 に依存するなら,パラメータ
に依存するなら,パラメータ 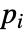 は
は 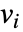 で置換される.
で置換される.
例題
すべて開くすべて閉じる例 (5)
スコープ (2)
アプリケーション (1)
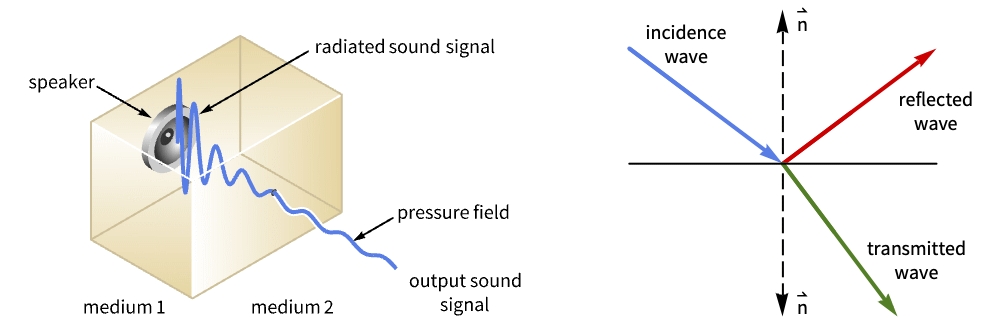
以下の音響モデルは,振動ピストンがパイプの一端の内側に配置され,パイプの他端は無限領域に開いている,開管を表している.また,無条件領域をモデル化するためにインポーダンス境界条件が片端に置かれている.モデル化される管は,以下の図で示すように,フランジが付いた円管である:
管の形状と境界条件は ![]() 軸について回転対称なので,軸対称モデルを使うことができる.音波の電波を表す支配方程式は軸対称ヘルムホルツ方程式である.
軸について回転対称なので,軸対称モデルを使うことができる.音波の電波を表す支配方程式は軸対称ヘルムホルツ方程式である.
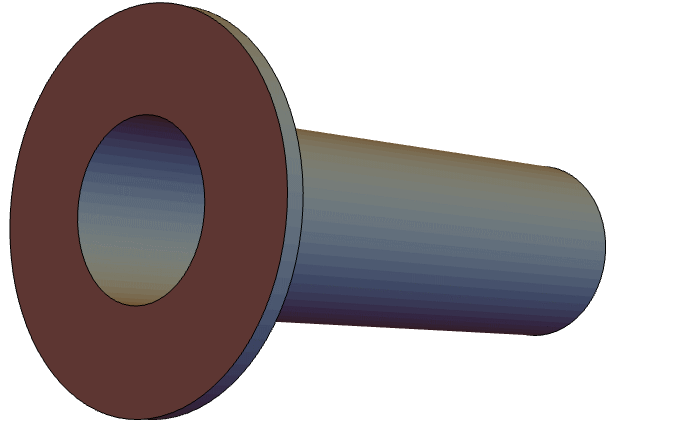
軸対称の形状は,![]() 平面における管の断面を表す2Dの矩形で近似できる:
平面における管の断面を表す2Dの矩形で近似できる:
このモデルには2つの境界条件がある.一つは ![]() でピストンの加速
でピストンの加速 ![]() を表すNeumannValueである:
を表すNeumannValueである:
2番目の境界条件はインピーダンス ![]() のAcousticImpedanceValueである.インピーダンス
のAcousticImpedanceValueである.インピーダンス ![]() は以下の近似で与えられる.
は以下の近似で与えられる.![]() は波数である:
は波数である:
![]() で定義されたMaxCellMeasureおよび解像度12を使用して
で定義されたMaxCellMeasureおよび解像度12を使用して ![]() でPDEを解き,正確な結果を取得する:
でPDEを解き,正確な結果を取得する:
考えられる問題 (1)
"SpecificAcousticImpedance"のデフォルト値はInfinityである:
テキスト
Wolfram Research (2020), AcousticImpedanceValue, Wolfram言語関数, https://reference.wolfram.com/language/ref/AcousticImpedanceValue.html.
CMS
Wolfram Language. 2020. "AcousticImpedanceValue." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/AcousticImpedanceValue.html.
APA
Wolfram Language. (2020). AcousticImpedanceValue. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/AcousticImpedanceValue.html