ActivePrediction[f,{conf1,conf2, …}]
gives an object representing the result of active prediction obtained by using the function f to determine values for the example configurations confi.
ActivePrediction[f,reg]
generates configurations within the region specified by reg.
ActivePrediction[f,sampler]
generates configurations by applying the function sampler.
ActivePrediction[f,{conf1,conf2,…}nsampler]
applies the function nsampler to successively generate configurations starting from one of the confi.


ActivePrediction
ActivePrediction[f,{conf1,conf2, …}]
gives an object representing the result of active prediction obtained by using the function f to determine values for the example configurations confi.
ActivePrediction[f,reg]
generates configurations within the region specified by reg.
ActivePrediction[f,sampler]
generates configurations by applying the function sampler.
ActivePrediction[f,{conf1,conf2,…}nsampler]
applies the function nsampler to successively generate configurations starting from one of the confi.
Details and Options
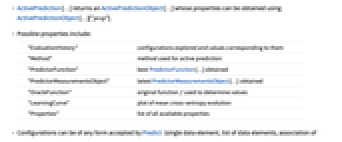


- ActivePrediction[…] returns an ActivePredictionObject[…] whose properties can be obtained using ActivePredictionObject[…]["prop"].
- Possible properties include:
-
"EvaluationHistory" configurations explored and values corresponding to them "Method" method used for active prediction "PredictorFunction" best PredictorFunction[…] obtained "PredictorMeasurementsObject" latest PredictorMeasurementsObject[…] obtained "OracleFunction" original function f used to determine values "LearningCurve" plot of mean cross-entropy evolution "Properties" list of all available properties - Configurations can be of any form accepted by Predict (single data element, list of data elements, association of data elements, etc.) and of any type accepted by Predict (numerical, textual, sounds, images, etc.).
- When applied to a configuration conf, the output of the function f must be a real-number value.
- In ActivePrediction[f,spec], spec defines the domain of the function f. A domain can be defined by a list of configurations, a geometric region or a configuration generator function.
- In ActivePrediction[f,sampler], sampler[] must output a configuration suitable for f to be applied to it.
- In ActivePrediction[f,{conf1,conf2,…}nsampler], nsampler[conf] must output a configuration.
- ActivePrediction has the same options as Predict, with the following additions and changes: [List of all options]
-
InitialEvaluationHistory None initial set of configurations and values MaxIterations 2000 maximum number of iterations Method Automatic method used to determine configurations to query and the prediction algorithm to use RandomSeeding 1234 what seeding of pseudorandom generators should be done internally - Possible settings for Method include:
-
Automatic automatically choose method "Randomized" choose random configurations from the domain "MaxEntropy" choose configurations for which the predictor has maximum uncertainty assoc association specifying the evaluation strategy and prediction method - In the form Methodassoc, the association can have elements:
-
"EvaluationStrategy" method for determining which configurations to query "PredictionMethod" method to use for prediction - Possible settings for RandomSeeding include:
-
Automatic automatically reseed every time the function is called Inherited use externally seeded random numbers seed use an explicit integer or strings as a seed -
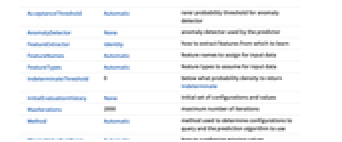
AcceptanceThreshold Automatic rarer probability threshold for anomaly detector AnomalyDetector None anomaly detector used by the predictor FeatureExtractor Identity how to extract features from which to learn FeatureNames Automatic feature names to assign for input data FeatureTypes Automatic feature types to assume for input data IndeterminateThreshold 0 below what probability density to return Indeterminate InitialEvaluationHistory None initial set of configurations and values MaxIterations 2000 maximum number of iterations Method Automatic method used to determine configurations to query and the prediction algorithm to use MissingValueSynthesis Automatic how to synthesize missing values PerformanceGoal Automatic aspects of performance to try to optimize RandomSeeding 1234 what seeding of pseudorandom generators should be done internally RecalibrationFunction Automatic how to post-process predicted value TargetDevice "CPU" the target device on which to perform training TimeGoal Automatic how long to spend training the classifier TrainingProgressReporting Automatic how to report progress during training UtilityFunction Automatic utility as function of actual and predicted value ValidationSet Automatic data on which to validate the model generated
List of all options
Examples
open all close allBasic Examples (3)
Train an ActivePredictionObject[…] to find the predictor for a function, given a set of configurations:
Extract the resulting predictor:
Train a prediction object to find the predictor for a function whose domain is defined by an interval:
Train a prediction object to find the predictor for the Det function, with the domain defined by a configuration generator:
Scope (3)
Train a prediction object to find a predictor for the sine function in an interval:
Obtain the list of available object properties:
Obtain the history of explored configurations:
Obtain the predictors trained during active prediction, along with some of their properties:
Obtain the method used to choose configurations to add to the training set:
Display the performances of the predictors trained during active prediction:
Visualize the predictions of the predictor on new examples:
Train a prediction object to find the predictor for a function that computes the color distance between a given color and the red color, with the domain defined by a random color generator:
Display the performances of the predictors trained during active prediction:
Display the comparison plot of the predictor for a test set:
Define a nontrivial function, with the domain defined by a neighborhood configuration generator:
Train a prediction object to find a predictor for the function, starting with some initial configurations:
Visualize the predictions of the predictor. It provides a good model of the function in the neighborhood of the initial configurations:
Options (3)
InitialEvaluationHistory (1)
Define a quadratic function whose domain is defined by a set of numbers:
Construct an initial "training set":
Train a prediction object to find a predictor for the function using the preceding information:
The examples in the first row in the training history now correspond to the initial training set:
MaxIterations (1)
Method (1)
Define a nontrivial stochastic function:
Train a prediction object by specifying the method as an association, choosing the evaluation strategy and the prediction method:
Specify a different method for active prediction:
Visualize the predictions of the two predictors. "GaussianProcess" produces a smoother predictor relative to "NearestNeighbors":
Applications (2)
Efficiently train a model to predict the elevation at a specific location:
Sample 1000 random locations to test the quality of the model:
Compare the predicted elevation versus the actual elevation obtained via a server call:
LogLikelihood Function Predictor (1)
Load Fisher's Iris dataset and divide it into a training set and a test set:
Construct a LogLikelihood function that trains a classifier on the training sample and then gives the "LogLikelihoodRate" on the test sample for a given choice of the hyperparameters:
Train a prediction object to find a predictor for the LogLikelihood function over a rectangular domain:
Obtain the coordinates of the explored configurations and their values:
Visualize the prediction of the predictor together with the explored configurations:
Related Guides
Text
Wolfram Research (2017), ActivePrediction, Wolfram Language function, https://reference.wolfram.com/language/ref/ActivePrediction.html (updated 2017).
CMS
Wolfram Language. 2017. "ActivePrediction." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2017. https://reference.wolfram.com/language/ref/ActivePrediction.html.
APA
Wolfram Language. (2017). ActivePrediction. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ActivePrediction.html
BibTeX
@misc{reference.wolfram_2025_activeprediction, author="Wolfram Research", title="{ActivePrediction}", year="2017", howpublished="\url{https://reference.wolfram.com/language/ref/ActivePrediction.html}", note=[Accessed: 23-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_activeprediction, organization={Wolfram Research}, title={ActivePrediction}, year={2017}, url={https://reference.wolfram.com/language/ref/ActivePrediction.html}, note=[Accessed: 23-January-2026]}