ArcCurvature[{x1,…,xn},t]
给出参数化曲线的曲率,其中该参数化曲线的笛卡儿坐标 xi 为 t 的函数.
ArcCurvature[{x1,…,xn},t,chart]
将 xi 解释为指定坐标图中的坐标.


ArcCurvature
ArcCurvature[{x1,…,xn},t]
给出参数化曲线的曲率,其中该参数化曲线的笛卡儿坐标 xi 为 t 的函数.
ArcCurvature[{x1,…,xn},t,chart]
将 xi 解释为指定坐标图中的坐标.
更多信息
- 圆弧的曲率有时也被称为无符号曲率或弗莱纳 (Frenet) 曲率.
- 在三维欧几里德空间中的曲线
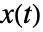 的圆弧曲率由
的圆弧曲率由 ![(TemplateBox[{{{{x, ^, {(, ', )}}, (, t, )}, x, {{x, ^, {(, {', '}, )}}, , {(, t, )}}}}, Norm])/(TemplateBox[{{{x, ^, {(, ', )}}, (, t, )}}, Norm]^3) (TemplateBox[{{{{x, ^, {(, ', )}}, (, t, )}, x, {{x, ^, {(, {', '}, )}}, , {(, t, )}}}}, Norm])/(TemplateBox[{{{x, ^, {(, ', )}}, (, t, )}}, Norm]^3)](Files/ArcCurvature.zh/2.png) 给出.
给出. - 在一般的空间中,曲线
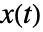 的圆弧曲率由
的圆弧曲率由 ![TemplateBox[{{{D, /, {(, {D, , t}, )}}, {{(, { , {{x, ^, {(, ', )}}, (, t, )}}, )}, /, {(, TemplateBox[{{{x, ^, {(, ', )}}, (, t, )}}, Norm], )}}}}, Norm] TemplateBox[{{{D, /, {(, {D, , t}, )}}, {{(, { , {{x, ^, {(, ', )}}, (, t, )}}, )}, /, {(, TemplateBox[{{{x, ^, {(, ', )}}, (, t, )}}, Norm], )}}}}, Norm]](Files/ArcCurvature.zh/4.png) 给出.
给出. - 在 ArcCurvature[x,t] 中,如果 x 是标量,ArcCurvature 则返回参数化曲线 {t,x} 的曲率.
- 在 ArcCurvature 的第三个参数中的坐标图可以用三元组 {coordsys,metric,dim} 的形式指定,就像指定CoordinateChartData 的第一个参数一样. 可以使用省略 dim 的短形式.
范例
打开所有单元 关闭所有单元范围 (5)
属性和关系 (2)
ArcCurvature 仅返回一个单一曲率:
FrenetSerretSystem 返回在维度 ![]() 上的所有
上的所有 ![]() 个曲率:
个曲率:
ArcCurvature 无符号:
从 FrenetSerretSystem 提取有符号的二维曲率:
参见
FrenetSerretSystem ArcLength CoordinateChartData KnotData D CoordinateTransform
Function Repository: Curvature CurvaturePlot Geodesic
相关指南
-
▪
- 向量分析
文本
Wolfram Research (2014),ArcCurvature,Wolfram 语言函数,https://reference.wolfram.com/language/ref/ArcCurvature.html.
CMS
Wolfram 语言. 2014. "ArcCurvature." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/ArcCurvature.html.
APA
Wolfram 语言. (2014). ArcCurvature. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/ArcCurvature.html 年
BibTeX
@misc{reference.wolfram_2025_arccurvature, author="Wolfram Research", title="{ArcCurvature}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/ArcCurvature.html}", note=[Accessed: 15-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_arccurvature, organization={Wolfram Research}, title={ArcCurvature}, year={2014}, url={https://reference.wolfram.com/language/ref/ArcCurvature.html}, note=[Accessed: 15-February-2026]}