ArcSech[z]
gives the inverse hyperbolic secant ![]() of the complex number
of the complex number ![]() .
.




ArcSech
ArcSech[z]
gives the inverse hyperbolic secant ![]() of the complex number
of the complex number ![]() .
.
Details
- Mathematical function, suitable for both symbolic and numerical manipulation.
- For certain special arguments, ArcSech automatically evaluates to exact values.
- ArcSech can be evaluated to arbitrary numerical precision.
- ArcSech automatically threads over lists.
- ArcSech[z] has branch cut discontinuities in the complex
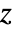 plane running from
plane running from 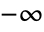 to
to 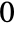 and
and 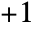 to
to 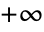 .
. - ArcSech can be used with Interval and CenteredInterval objects. »
Background & Context
- ArcSech is the inverse hyperbolic secant function. For a real number
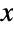 , ArcSec[x] represents the hyperbolic angle measure
, ArcSec[x] represents the hyperbolic angle measure 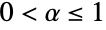 such that
such that 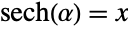 .
. - ArcSech automatically threads over lists. For certain special arguments, ArcSech automatically evaluates to exact values. When given exact numeric expressions as arguments, ArcSech may be evaluated to arbitrary numeric precision. Operations useful for manipulation of symbolic expressions involving ArcSech include FunctionExpand, TrigToExp, TrigExpand, Simplify, and FullSimplify.
- ArcSech is defined for complex argument
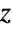 by
by 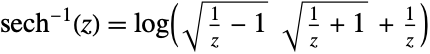 . ArcSech[z] has branch cut discontinuities in the complex
. ArcSech[z] has branch cut discontinuities in the complex 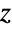 plane.
plane. - Related mathematical functions include Sech, ArcCsch, and ArcSec.
Examples
open all close allBasic Examples (6)
Plot over a subset of the reals:
Plot over a subset of the complexes:
Series expansion at the origin:
Asymptotic expansion at Infinity:
Scope (40)
Numerical Evaluation (6)
The precision of the output tracks the precision of the input:
Evaluate for complex arguments:
Evaluate ArcSech efficiently at high precision:
Compute worst-case guaranteed intervals using Interval and CenteredInterval objects:
Or compute average-case statistical intervals using Around:
Compute the elementwise values of an array:
Or compute the matrix ArcSech function using MatrixFunction:
Specific Values (4)
Visualization (3)
Function Properties (10)
ArcSech is defined for all real values from the interval ![]() :
:
ArcSech achieves all real values greater than or equal to 0:
Function range for arguments from the complex domain:
ArcSech is not an analytic function:
ArcSech is decreasing over its real domain:
ArcSech is injective:
ArcSech is not surjective:
ArcSech is non-negative over its real domain:
It has both singularity and discontinuity in (-∞,0] and [1,∞):
ArcSech is neither convex nor concave:
TraditionalForm formatting:
Integration (3)
Series Expansions (3)
Function Identities and Simplifications (3)
Function Representations (5)
Represent using ArcCosh:
Representation through inverse Jacobi functions:
Represent using Hypergeometric2F1:
ArcSech can be represented in terms of MeijerG:
ArcSech can be represented as a DifferentialRoot:
Properties & Relations (2)
Compose with inverse functions:
Use PowerExpand to disregard multivaluedness of the ArcSech:
Alternatively, evaluate under additional assumptions:
Use TrigToExp to express in terms of logarithm:
See Also
Tech Notes
Related Guides
Related Links
History
Introduced in 1988 (1.0) | Updated in 2021 (13.0)
Text
Wolfram Research (1988), ArcSech, Wolfram Language function, https://reference.wolfram.com/language/ref/ArcSech.html (updated 2021).
CMS
Wolfram Language. 1988. "ArcSech." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2021. https://reference.wolfram.com/language/ref/ArcSech.html.
APA
Wolfram Language. (1988). ArcSech. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ArcSech.html
BibTeX
@misc{reference.wolfram_2025_arcsech, author="Wolfram Research", title="{ArcSech}", year="2021", howpublished="\url{https://reference.wolfram.com/language/ref/ArcSech.html}", note=[Accessed: 07-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_arcsech, organization={Wolfram Research}, title={ArcSech}, year={2021}, url={https://reference.wolfram.com/language/ref/ArcSech.html}, note=[Accessed: 07-February-2026]}