AugmentedSymmetricPolynomial[{r1,r2,…}]
形式的で引数のある,指数 r1, r2, …の対称式を表す.
AugmentedSymmetricPolynomial[{{r11,…,r1n},{r21,…,r2n},…}]
多変量かつ形式的で引数のある,指数ベクトルが{r11, …, r1n}, {r21, …, r2n}, …の対称式を表す.
AugmentedSymmetricPolynomial[rspec,data]
data 中の引数のある対称式を返す.


AugmentedSymmetricPolynomial
AugmentedSymmetricPolynomial[{r1,r2,…}]
形式的で引数のある,指数 r1, r2, …の対称式を表す.
AugmentedSymmetricPolynomial[{{r11,…,r1n},{r21,…,r2n},…}]
多変量かつ形式的で引数のある,指数ベクトルが{r11, …, r1n}, {r21, …, r2n}, …の対称式を表す.
AugmentedSymmetricPolynomial[rspec,data]
data 中の引数のある対称式を返す.
詳細

- AugmentedSymmetricPolynomial[{r1,…,rk},{x1,…,xn}]は
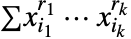 で与えられる.このとき,指数集合
で与えられる.このとき,指数集合 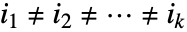 および
および について総和が求められる.
について総和が求められる. - 多変量の場合,riと xiはベクトルであり,xiriは xi1ri1xi2ri2⋯であると解釈される.
- AugmentedSymmetricPolynomial[rspec]を使ってモーメント推定に使われる形式的な引数のある対称和を表すことができる.
- MomentConvertを使ってAugmentedSymmetricPolynomialオブジェクトによるモーメント推定器が生成できる.
- MomentEvaluateを使ってデータ集合の形式的なAugmentedSymmetricPolynomialオブジェクトについての多項式が評価できる.
例題
すべて開く すべて閉じる例 (1)
スコープ (2)
アプリケーション (1)
AugmentedSymmetricPolynomialの多項式を線形化する:
特性と関係 (1)
関連するガイド
テキスト
Wolfram Research (2010), AugmentedSymmetricPolynomial, Wolfram言語関数, https://reference.wolfram.com/language/ref/AugmentedSymmetricPolynomial.html.
CMS
Wolfram Language. 2010. "AugmentedSymmetricPolynomial." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/AugmentedSymmetricPolynomial.html.
APA
Wolfram Language. (2010). AugmentedSymmetricPolynomial. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/AugmentedSymmetricPolynomial.html
BibTeX
@misc{reference.wolfram_2025_augmentedsymmetricpolynomial, author="Wolfram Research", title="{AugmentedSymmetricPolynomial}", year="2010", howpublished="\url{https://reference.wolfram.com/language/ref/AugmentedSymmetricPolynomial.html}", note=[Accessed: 03-March-2026]}
BibLaTeX
@online{reference.wolfram_2025_augmentedsymmetricpolynomial, organization={Wolfram Research}, title={AugmentedSymmetricPolynomial}, year={2010}, url={https://reference.wolfram.com/language/ref/AugmentedSymmetricPolynomial.html}, note=[Accessed: 03-March-2026]}