Beta
詳細

- Betaは記号操作・数値操作の両方に適した数学関数である.
-
![TemplateBox[{a, b}, Beta]=TemplateBox[{a}, Gamma]TemplateBox[{b}, Gamma]/TemplateBox[{{a, +, b}}, Gamma]=int_0^1t^(a-1)(1-t)^(b-1)dt TemplateBox[{a, b}, Beta]=TemplateBox[{a}, Gamma]TemplateBox[{b}, Gamma]/TemplateBox[{{a, +, b}}, Gamma]=int_0^1t^(a-1)(1-t)^(b-1)dt](Files/Beta.ja/3.png)
-
![TemplateBox[{z, a, b}, Beta3]=int_0^zt^(a-1)(1-t)^(b-1)dt TemplateBox[{z, a, b}, Beta3]=int_0^zt^(a-1)(1-t)^(b-1)dt](Files/Beta.ja/4.png)
- Beta[z,a,b]は,複素
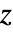 平面上に,
平面上に, 〜
〜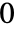 の範囲で不連続な分枝切断線を持つ.
の範囲で不連続な分枝切断線を持つ. - Beta[z0,z1,a,b]は,一般的不完全ベータ関数
 を与える.
を与える. - 不完全ベータ(Beta)関数の引数は,不完全ガンマ(Gamma)関数と異なった並び順をすることに注意.
- 特別な引数の場合,Betaは,自動的に厳密値を計算する.
- Betaは任意の数値精度で評価できる.
- Betaは自動的にリストに縫い込まれる.
- TraditionalFormの設定では,\[CapitalBeta]を使ってBetaが表示される.
- BetaはIntervalオブジェクトおよびCenteredIntervalオブジェクトに使うことができる. »
例題
すべて開くすべて閉じる例 (6)
Infinityにおける級数展開:
スコープ (42)
数値評価 (8)
Betaを高精度で効率よく評価する:
IntervalオブジェクトとCenteredIntervalオブジェクトを使って最悪の場合に保証される区間を計算する:
Aroundを使って平均的な場合の統計区間を計算することもできる:
MatrixFunctionを使って行列のBeta関数を計算することもできる:
関数の特性 (11)
![]() は正の奇数
は正の奇数 ![]() については単射であるが,正の偶数
については単射であるが,正の偶数 ![]() についてはそうではない:
についてはそうではない:
![]() は正の奇数
は正の奇数 ![]() については全射であるが,正の偶数
については全射であるが,正の偶数 ![]() についてはそうではない:
についてはそうではない:
![]() は正の偶数
は正の偶数 ![]() については非負であるが奇数
については非負であるが奇数 ![]() については不定である:
については不定である:
TraditionalFormによる表示:
級数展開 (5)
関数の恒等式と簡約 (4)
関数表現 (6)
Gamma関数による主定義:
BetaはDifferentialRootとして表すことができる:
一般化と拡張 (6)
オイラーのベータ関数 (2)
アプリケーション (5)
特性と関係 (7)
オイラーのベータ関数をオイラーのガンマ関数の割合として表す:
FullSimplifyを使ってベータ関数を簡約する:
Betaを含む式の総和を求める:
BetaはDifferentialRootとして表すことができる:
考えられる問題 (4)
大きい引数は,明示的に計算するのには小さすぎる結果を与えることがある:
アルゴリズムを使って生成した結果では,ベータ関数ではなくガンマ関数や超幾何関数が使われることがよくある:
一般に,FullSimplifyではベータ関数は生成されない:
おもしろい例題 (2)
複素平面上でBetaをネストさせる:
テキスト
Wolfram Research (1988), Beta, Wolfram言語関数, https://reference.wolfram.com/language/ref/Beta.html (2022年に更新).
CMS
Wolfram Language. 1988. "Beta." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2022. https://reference.wolfram.com/language/ref/Beta.html.
APA
Wolfram Language. (1988). Beta. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Beta.html