CanonicalizePolygon
CanonicalizePolygon[poly]
共通座標および内側と外側の境界で表す多角形 poly の正準表現を与える.
CanonicalizePolygon[poly,"filter"]
指定されたフィルタをかけた poly の正準表現を与える.
詳細

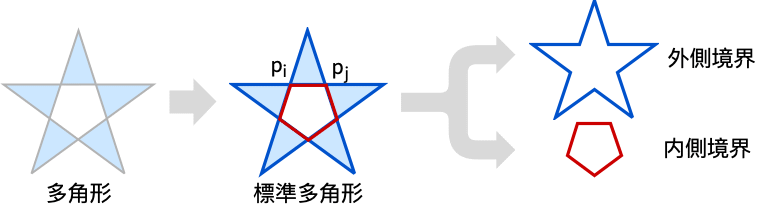
- CanonicalizePolygonは,さまざまな表現や説明から多角形の単純な標準表現を得るのに使われる.
- CanonicalizePolygonは,多角形を最適化された標準形Polygon[{p1,p2,…},{outer1,outer2inner2,…}]に変換する.
- 点 piは交差しない線分の端点で,Sort順にソートされる.
- 外側境界 outerkは,端点で接触している可能性はあるがその他の交差はない線分{pi,pj}の閉曲線である.
- 内側境界 innerkは,端点で接触している可能性はあるがその他の交差はない線分{pi,pj}の閉曲線である.
- 一般的な多角形指定で,線および点を表す退化した多角形を与えることができる."filter"指定を使うことで,これらの低次元成分を保持するかどうかが制御できる.
- 次は,可能な"filter"指定である.
-
All 線や点を含む全成分 
Full 全次元成分のみ
例題
すべて開くすべて閉じる例 (1)
Polygonの正準形を求める:
スコープ (9)
基本的な用法 (7)
CanonicalizePolygonは多角形に使うことができる:
CanonicalizePolygonは地理実体の多角形に使うことができる:
GeoPositionを使った多角形:
GeoPositionXYZを使った多角形:
GeoPositionENUを使った多角形:
GeoGridPositionを使った多角形:
特性と関係 (4)
CanonicalizePolygonを使ってPolygonCoordinatesを得る:
単純多角形の CanonicalizePolygonは多角形座標の数を保存している:
OuterPolygonは外側多角形の正準表現を与える:
InnerPolygonは内側多角形の正準表現を与える:
考えられる問題 (1)
CanonicalizePolygonは幾何領域にのみ使うことができる:
テキスト
Wolfram Research (2019), CanonicalizePolygon, Wolfram言語関数, https://reference.wolfram.com/language/ref/CanonicalizePolygon.html.
CMS
Wolfram Language. 2019. "CanonicalizePolygon." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/CanonicalizePolygon.html.
APA
Wolfram Language. (2019). CanonicalizePolygon. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/CanonicalizePolygon.html