CanonicalizePolyhedron

CanonicalizePolyhedron[poly]

gives a canonical representation of the polyhedron poly with shared coordinates and with inner and outer boundaries.

Details

  • CanonicalizePolyhedron is used to get a simple standard representation of a polyhedron from various representations and descriptions.
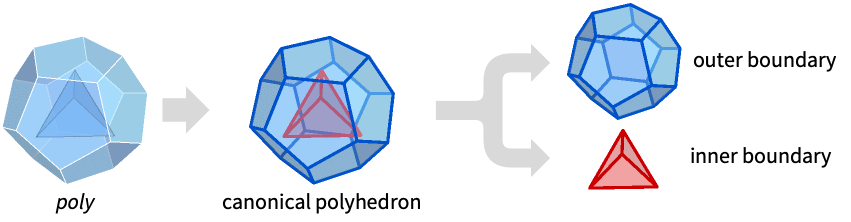
  • CanonicalizePolyhedron converts a polyhedron to an optimized standard form Polyhedron[{p1,p2,…},{outer1,outer2inner2,…}].
  • The points pi are the vertex points of non-intersecting polygonal faces and sorted into Sort order.
  • An outer boundary outeri is a closed surface with polygonal faces {fi1,fi2,…}, possibly touching at edges.
  • An inner boundary inneri is a closed surface with polygonal faces {fj1,fj2,…}, possibly touching at edges.

Examples

open allclose all

Basic Examples  (1)

Find the canonical form of a Polyhedron:

Scope  (3)

CanonicalizePolyhedron works on polyhedra:

Tetrahedron:

Octahedron:

Polyhedron with voids:

Polyhedrons with disconnected components:

Applications  (1)

Set up a graphics complex with shared coordinates:

Properties & Relations  (5)

Using CanonicalizePolyhedron to get PolyhedronCoordinates:

The CanonicalizePolyhedron of a platonic solid is a polyhedron:

The CanonicalizePolyhedron of simple polyhedra preserve the number of polyhedron coordinates:

OuterPolyhedron gives the canonical representation of the outer polyhedron:

InnerPolyhedron gives the canonical representation of the inner polyhedron:

Possible Issues  (1)

CanonicalizePoyhedron works only on geometric regions:

Wolfram Research (2019), CanonicalizePolyhedron, Wolfram Language function, https://reference.wolfram.com/language/ref/CanonicalizePolyhedron.html.

Text

Wolfram Research (2019), CanonicalizePolyhedron, Wolfram Language function, https://reference.wolfram.com/language/ref/CanonicalizePolyhedron.html.

CMS

Wolfram Language. 2019. "CanonicalizePolyhedron." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/CanonicalizePolyhedron.html.

APA

Wolfram Language. (2019). CanonicalizePolyhedron. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/CanonicalizePolyhedron.html

BibTeX

@misc{reference.wolfram_2024_canonicalizepolyhedron, author="Wolfram Research", title="{CanonicalizePolyhedron}", year="2019", howpublished="\url{https://reference.wolfram.com/language/ref/CanonicalizePolyhedron.html}", note=[Accessed: 28-April-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_canonicalizepolyhedron, organization={Wolfram Research}, title={CanonicalizePolyhedron}, year={2019}, url={https://reference.wolfram.com/language/ref/CanonicalizePolyhedron.html}, note=[Accessed: 28-April-2024 ]}