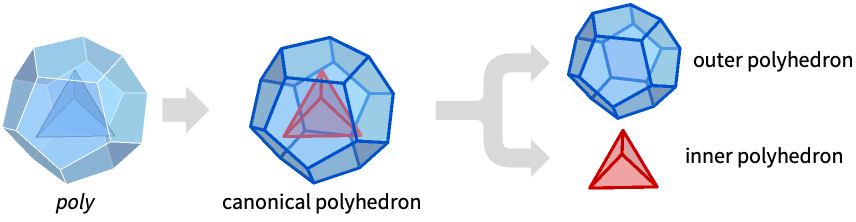
InnerPolyhedron

InnerPolyhedron[poly]

gives the inner polyhedron of the polyhedron poly.

Details

  • InnerPolyhedron is also known as polyhedron inner void.
  • Typically used to decompose a polyhedron as a difference of simple polyhedrons, even when the original construction of the polyhedron was using crossing polygon faces etc.
  • InnerPolyhedron is defined by the canonicalization performed in CanonicalizePolyhedron.
  • InnerPolyhedron gives a polyhedron of the form Polyhedron[{p1,p2,…}, {{f1,f2,…},…}], where pk are explicit coordinates, and fk are integer lists referring to polygon faces.
  • If poly is a polyhedron without a void, then the result is an EmptyRegion object.

Examples

open allclose all

Basic Examples  (1)

Get the inner polyhedron:

Scope  (3)

InnerPolyhedron works on polyhedrons:

Tetrahedron:

Hexahedron:

Polyhedron with holes:

Polyhedrons with disconnected components:

Properties & Relations  (1)

InnerPolyhedron of a simple polyhedron is an empty polyhedron:

Wolfram Research (2019), InnerPolyhedron, Wolfram Language function, https://reference.wolfram.com/language/ref/InnerPolyhedron.html.

Text

Wolfram Research (2019), InnerPolyhedron, Wolfram Language function, https://reference.wolfram.com/language/ref/InnerPolyhedron.html.

CMS

Wolfram Language. 2019. "InnerPolyhedron." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/InnerPolyhedron.html.

APA

Wolfram Language. (2019). InnerPolyhedron. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/InnerPolyhedron.html

BibTeX

@misc{reference.wolfram_2024_innerpolyhedron, author="Wolfram Research", title="{InnerPolyhedron}", year="2019", howpublished="\url{https://reference.wolfram.com/language/ref/InnerPolyhedron.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_innerpolyhedron, organization={Wolfram Research}, title={InnerPolyhedron}, year={2019}, url={https://reference.wolfram.com/language/ref/InnerPolyhedron.html}, note=[Accessed: 21-November-2024 ]}