CarlsonRD

CarlsonRD[x,y,z]

gives the Carlson's elliptic integral TemplateBox[{x, y, z}, CarlsonRD].

Details

  • Mathematical function, suitable for both symbolic and numerical manipulation.
  • For non-negative arguments, TemplateBox[{x, y, z}, CarlsonRD]⩵3/2int_0^infty(t+x)^(-1/2)(t+y)^(-1/2)(t+z)^(-3/2)dt.
  • CarlsonRD[x,y,z] has a branch cut discontinuity at .
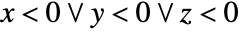  • For certain arguments, CarlsonRD automatically evaluates to exact values.
  • CarlsonRD can be evaluated to arbitrary precision.
  • CarlsonRD automatically threads over lists.
  • CarlsonRD can be used with Interval and CenteredInterval objects. »

Examples

open allclose all

Basic Examples  (3)

Evaluate numerically:

Plot CarlsonRD:

CarlsonRD is related to a combination of Legendre elliptic integrals restricted to :

Scope  (15)

Numerical Evaluation  (6)

Evaluate CarlsonRD numerically:

Evaluate to high precision:

The precision of the output tracks the precision of the input:

Evaluate for complex arguments:

Evaluate efficiently at high precision:

CarlsonRD threads elementwise over lists:

CarlsonRD can be used with Interval and CenteredInterval objects:

Specific Values  (2)

Simple exact values are generated automatically:

When one argument of CarlsonRD is zero, CarlsonRD can be expressed in terms of the complete elliptic integrals CarlsonRE and CarlsonRK:

Differentiation and Integration  (2)

Derivative of TemplateBox[{x, y, z}, CarlsonRD] with respect to :

Derivative of TemplateBox[{x, y, z}, CarlsonRD] with respect to :

Indefinite integral of TemplateBox[{x, y, z}, CarlsonRD] with respect to :

Indefinite integral of TemplateBox[{x, y, z}, CarlsonRD] with respect to :

Function Representations  (1)

TraditionalForm formatting:

Function Identities and Simplifications  (4)

An equation relating CarlsonRD, CarlsonRF and CarlsonRG:

Some cyclic permutation identities for CarlsonRD:

CarlsonRD satisfies the Euler–Poisson partial differential equation:

CarlsonRD satisfies Euler's homogeneity relation:

Applications  (2)

Distance along a meridian of the Earth:

Compare with the result of GeoDistance:

Parametrization of a Mylar balloon (two flat sheets of plastic sewn together at their circumference and then inflated):

Properties & Relations  (1)

CarlsonRD is symmetric with respect to its first two arguments:

Wolfram Research (2021), CarlsonRD, Wolfram Language function, https://reference.wolfram.com/language/ref/CarlsonRD.html (updated 2023).

Text

Wolfram Research (2021), CarlsonRD, Wolfram Language function, https://reference.wolfram.com/language/ref/CarlsonRD.html (updated 2023).

CMS

Wolfram Language. 2021. "CarlsonRD." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2023. https://reference.wolfram.com/language/ref/CarlsonRD.html.

APA

Wolfram Language. (2021). CarlsonRD. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/CarlsonRD.html

BibTeX

@misc{reference.wolfram_2024_carlsonrd, author="Wolfram Research", title="{CarlsonRD}", year="2023", howpublished="\url{https://reference.wolfram.com/language/ref/CarlsonRD.html}", note=[Accessed: 21-December-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_carlsonrd, organization={Wolfram Research}, title={CarlsonRD}, year={2023}, url={https://reference.wolfram.com/language/ref/CarlsonRD.html}, note=[Accessed: 21-December-2024 ]}