ClebschGordan

ClebschGordan[{j1,m1},{j2,m2},{j,m}]

gives the Clebsch–Gordan coefficient for the decomposition of in terms of .

Details

  • The Clebsch–Gordan coefficients vanish except when 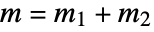and the 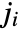satisfy a triangle inequality.
  • The parameters of ClebschGordan can be integers, half‐integers, or symbolic expressions.
  • The Wolfram Language uses the standard conventions of Edmonds for the phase of the Clebsch–Gordan coefficients.
  • The Clebsch–Gordan coefficients and 3‐ 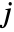symbols in the Wolfram Language satisfy the relation .

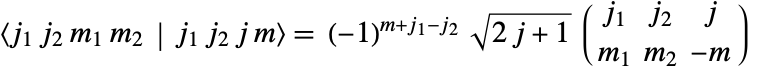Examples

open allclose all

Basic Examples  (2)

Evaluate a Clebsch–Gordan coefficient with integer arguments:

Use symbolic arguments to obtain exact symbolic answers:

Scope  (2)

ClebschGordan works with integer and half‐integer arguments:

For symbolic input ClebschGordan evaluates to ThreeJSymbol:

Applications  (3)

Plot Clebsch–Gordan coefficients as a function of and :

Decompose a spherical harmonic into a sum of products of two spherical harmonics:

Apply angular momentum operators to spherical harmonics:

Properties & Relations  (2)

Evaluate the completely symbolic case of ClebschGordan:

Demonstrate ‐sum orthogonality:

Possible Issues  (1)

A message is issued and the result of 0 is returned when :

Neat Examples  (1)

Visualize contours constructed from Clebsch–Gordan coefficients:

Wolfram Research (1991), ClebschGordan, Wolfram Language function, https://reference.wolfram.com/language/ref/ClebschGordan.html.

Text

Wolfram Research (1991), ClebschGordan, Wolfram Language function, https://reference.wolfram.com/language/ref/ClebschGordan.html.

CMS

Wolfram Language. 1991. "ClebschGordan." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/ClebschGordan.html.

APA

Wolfram Language. (1991). ClebschGordan. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ClebschGordan.html

BibTeX

@misc{reference.wolfram_2025_clebschgordan, author="Wolfram Research", title="{ClebschGordan}", year="1991", howpublished="\url{https://reference.wolfram.com/language/ref/ClebschGordan.html}", note=[Accessed: 05-May-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_clebschgordan, organization={Wolfram Research}, title={ClebschGordan}, year={1991}, url={https://reference.wolfram.com/language/ref/ClebschGordan.html}, note=[Accessed: 05-May-2025 ]}