WignerD

WignerD[{j,m1,m2},ψ,θ,ϕ]

gives the Wigner D-function .

WignerD[{j,m1,m2},θ,ϕ]

gives the Wigner D-function .

WignerD[{j,m1,m2},θ]

gives the Wigner D-function .

Details

  • The Wigner D-function 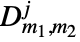gives the matrix element of a rotation operator parametrized by Euler angles in a 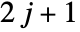–dimensional unitary representation of a rotation group when parameters 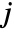, , 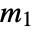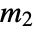are physical, i.e. all integers or half-integers such that .
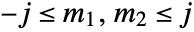  • For unphysical parameters, WignerD is defined by an analytic continuation.
  • The Wolfram Language uses phase conventions where TemplateBox[{j, {m, _, 1}, {m, _, 2}, psi, theta, phi}, WignerD]=exp(ⅈ m_1 psi+ⅈ m_2phi) TemplateBox[{j, {m, _, 1}, {m, _, 2}, 0, theta, 0}, WignerD].

Examples

open allclose all

Basic Examples  (1)

Evaluate with integer-valued physical parameters:

Evaluate with physical parameters that are half-integers:

Scope  (1)

Evaluate numerically for physical parameters:

Generalizations & Extensions  (1)

Evaluate numerically for unphysical parameters:

Applications  (1)

Construct a rotation matrix for a spin-1/2 representation:

Check unitarity:

Build a 3D vector from spinors:

Spinor basis translates into the coordinate basis:

Coordinate transformation induced by unitary transformation on spinors:

Construct the resulting rotation matrix directly using Euler's angles:

Properties & Relations  (4)

For vanishing parameter m1, WignerD reduces to SphericalHarmonicY:

Matrix elements of the Wigner D-matrix satisfy certain symmetry relations:

WignerD functions form an orthogonal basis on the group:

The integral is equal to 2/(2 j_1+1) (4 pi)^2TemplateBox[{{{j, _, 1}, ,, {j, _, 2}}}, KroneckerDeltaSeq]TemplateBox[{{{m, _, {(, 11, )}}, ,, {m, _, {(, 21, )}}}}, KroneckerDeltaSeq]TemplateBox[{{{m, _, {(, 12, )}}, ,, {m, _, {(, 22, )}}}}, KroneckerDeltaSeq]:

The product of two WignerD functions can be expanded in terms of WignerD functions using ClebschGordan coefficients:

Wolfram Research (2010), WignerD, Wolfram Language function, https://reference.wolfram.com/language/ref/WignerD.html.

Text

Wolfram Research (2010), WignerD, Wolfram Language function, https://reference.wolfram.com/language/ref/WignerD.html.

CMS

Wolfram Language. 2010. "WignerD." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/WignerD.html.

APA

Wolfram Language. (2010). WignerD. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/WignerD.html

BibTeX

@misc{reference.wolfram_2025_wignerd, author="Wolfram Research", title="{WignerD}", year="2010", howpublished="\url{https://reference.wolfram.com/language/ref/WignerD.html}", note=[Accessed: 21-February-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_wignerd, organization={Wolfram Research}, title={WignerD}, year={2010}, url={https://reference.wolfram.com/language/ref/WignerD.html}, note=[Accessed: 21-February-2025 ]}